热解炭涂层I-II复合型裂纹的应力强度因子分析

孙振国，刘 刚，张建辉

(杭州电子科技大学机械工程学院，浙江 杭州 310018)

0 引 言

人工机械心脏瓣膜是植入到人体心脏内的人工脏器，通过手术置换来挽救心脏瓣膜病患者的生命。热解炭具有耐磨、耐腐蚀以及优异的血液相容性等特点，所以人工心瓣瓣片大多采用热解炭石墨复合材料[1]。但是，在生产制备、加工、手术过程，以及心脏内承受血流循环冲击时，热解炭涂层表面可能会出现微小裂纹，长期工作中的裂纹可能发生扩展，甚至导致涂层脆性断裂，给患者的健康造成严重影响。因此，研究热解炭涂层裂纹对人工心瓣组件结构稳定性的影响尤为重要。目前，相关研究大多采用实验的方式，对热解炭涂层裂纹的模拟仿真较少。例如，R.O.Ritchie等[2]采用维克氏硬度计压头施加在热解炭表面产生裂纹的方法，研究人工心脏瓣膜的损伤容限并预测其使用寿命；C.B.Gilpin等[3]通过带预制裂纹的样品进行紧凑拉伸实验，研究热解炭及热解炭包覆石墨复合材料的断裂韧性。在复杂的心脏生理环境中，由于人工心瓣热解炭涂层裂纹扩展面与血流载荷不一定处于垂直状态，故涂层不是单纯的I型(张开型)或II型(滑开型)断裂，因此研究热解炭涂层I-II复合型裂纹更为合理。应力强度因子(Stress Intensity Factors, SIFs)是衡量带裂纹体内裂纹尖端附近弹性应力应变场强度的物理量，根据SIFs能够判断裂纹是否进入失稳状态[4]。为了研究人工心瓣热解炭涂层I-II复合型裂纹，本文采用ABAQUS有限元软件仿真热解炭涂层边缘裂纹和中心裂纹的I-II复合型SIFs，并讨论裂纹倾斜角、裂纹数量以及裂纹长度对SIFs的影响。

1 理论基础

根据裂纹扩展面受力方向的不同，可将裂纹分为张开型(I型)、滑开型(II型)以及撕开型(III型)，其中I型裂纹扩展平面与所受载荷垂直，II和III型裂纹扩展平面与载荷平行[5]。SIFs可表征裂纹尖端应力场和应变场强度，是判断裂纹是否进入失稳状态和计算裂纹扩展速率的重要参数。

ABAQUS有限元分析软件采用J积分法求解裂纹尖端SIFs，在线弹性断裂理论中J积分与路径无关[6]。J积分公式如下：

(1)

图1 J积分回路

式中，Γ为围绕裂纹尖端逆时针方向的封闭轮廓，W为应变能密度，T为封闭轮廓上的张力矢量，u为封闭轮廓位移矢量，s为封闭轮廓的弧长。J积分回路如图1所示。

在线弹性材料中，J积分和应力强度因子之间的关系可表示为[7]：

(2)

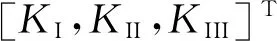
对于各向同性材料而言，B为对角线矩阵，式(2)简化为：

(3)

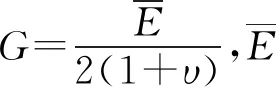
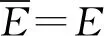
(4)

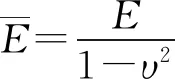
(5)

式中，E为弹性模量，υ为泊松比。

2 模型参数与网格划分

ABAQUS[8]是一套功能丰富、处理能力强大的有限元仿真软件，解决问题的范围包含线性问题以及复杂的非线性问题，通过ABAQUS软件进行结构力学分析可以高效精确地获得仿真结果。

2.1 模型几何参数

采用ABAQUS/CAE进行几何建模，模型尺寸如图2所示。图2中，2H和2W分别为模型的长度和宽度，2H=6W，2a为裂纹长度，β为裂纹面与载荷所成倾斜角。模型材料为低温各向同性热解炭，其弹性模量E=28 GPa，泊松比υ=0.3，平板两端受均匀拉应力σ=10 MPa。

2.2 网格划分

有限元网格划分包括较粗的全局网格和精细的局部网格。模型整体采用CPS8单元，即采用八结点双向二次平面应力四边形单元进行网格划分。由于裂纹尖端存在奇异性，仿真时裂尖单元采用1/4奇异单元，并对裂纹尖端的网格进行细化。通过将CPS6六结点二次平面应力三角形单元任意两边的中点向两边交点移动1/4的距离而形成1/4奇异单元，这种奇异单元满足裂纹尖端应力和应变1/4奇异性的要求[9]。裂纹尖分布的奇异性单元如图3所示。

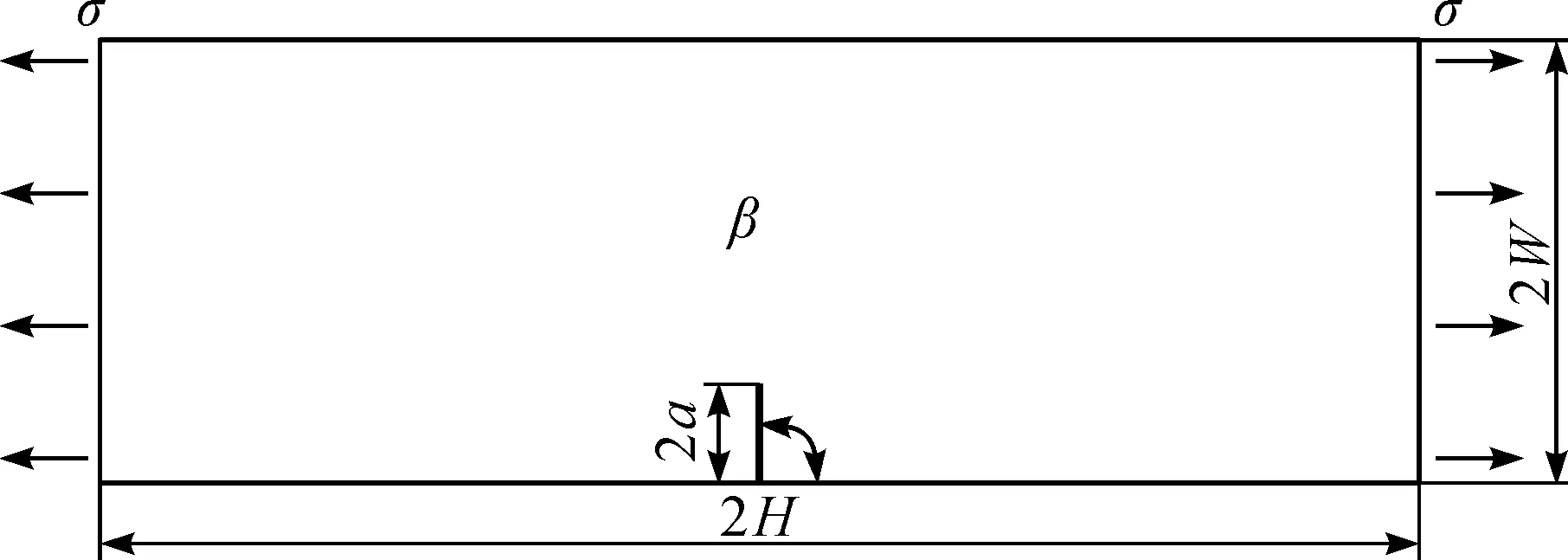
图2 有限元分析几何模型

图3 裂纹尖端奇异单元

3 仿真结果与分析

根据应力强度因子理论，裂纹形状、裂纹位置、裂纹数目等因素会影响SIFs[10]。本文通过改变裂纹倾斜角、裂纹长度与平板宽度比和裂纹数目来研究I-II复合型裂纹的SIFs。

3.1 可靠性验证

ABAQUS软件通过J积分法求解得到应力强度因子仿真值，并与应力强度因子手册[11]中基于实验基础的理论值进行对比。

在倾斜角β=90°，裂纹长度与平板宽度比a/W分别为0.1，0.2，0.3，0.4，0.5时，得到的KI仿真值与理论值如表1所示。

表1 ABAQUS中KI仿真值与理论值对比

由表1可知：仿真值与理论值最大相对误差不超过4%，说明基于ABAQUS有限元分析软件的仿真模拟具有合理性和可靠性。同时可以得出：在其他条件不变的情况下，a/W在[0.1，0.5]范围内，随着裂纹长度增加，KI值越大。

3.2 倾斜角对I-II复合型裂纹SIFs影响

边缘裂纹和中心裂纹的倾斜角β从0°～90°每隔15°重新建模分析，在a/W=0.3，β=90°时，边缘裂纹和中心裂纹尖端应力云图如图4所示。裂纹尖端出现应力集中现象，且米塞斯(Mises)应力值最大，并由裂尖向周围逐渐减小。

图4 a/W=0.3，β=90°时，边缘裂纹和中心裂纹尖端应力云图

边缘裂纹和中心裂纹I，II型SIFs随倾斜角β和裂纹长度与平板宽度比a/W改变时的变化规律分别如图5、图6所示。由图5、图6可知：(1)当裂纹长度不变时，KI随着倾斜角β增大而增大，β=0°时，载荷与裂纹面平行，KI为0。因为β增大引发I型裂纹的垂直载荷随之增大，故KI增大；(2)当裂纹长度不变时，随着倾斜角β增大，在β=45°时KII达到最大值，且倾斜角β=0°，β=15°和β=30°对应的KII曲线分别与倾斜角β=90°，β=75°和β=60°对应的KII曲线相重合；(3)当裂纹倾斜角β>0°时，边缘裂纹和中心裂纹KI随裂纹长度增加而变大；当裂纹倾斜角β不为0°和90°时，边缘裂纹和中心裂纹KII随裂纹长度增加而变大。

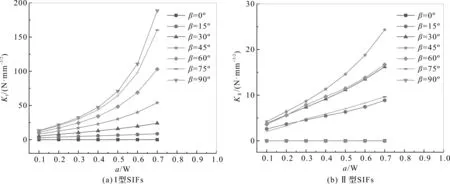
图5 倾斜角变化时，边缘裂纹I，II型SIFs

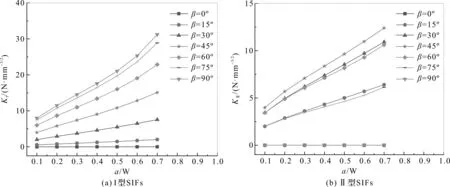
图6 倾斜角变化时，中心裂纹I，II型SIFs

3.3 裂纹数量对I-II复合型裂纹SIFs影响

保持倾斜角β=45°不变，裂纹数量n从1～7每隔2个数量级重新建模。a/W=0.3，β=45°，n=3时，边缘裂纹和中心裂纹尖端应力云图如图7所示。

图7 n=3时，边缘裂纹和中心裂纹尖端应力云图

在倾斜角β=45°的情况下，边缘裂纹和中心裂纹I、II型SIFs随裂纹数量n和裂纹长度与平板宽度比a/W改变时的变化规律如图8、图9所示。由图8、图9可知：(1)随着裂纹数量n的增加，边缘裂纹和中心裂纹的KI，KII曲线分别重合，且均小于单条裂纹情况下的KI，KII值；(2)在裂纹数量n不变的情况下，随着裂纹长度增大，KI，KII值也增大。

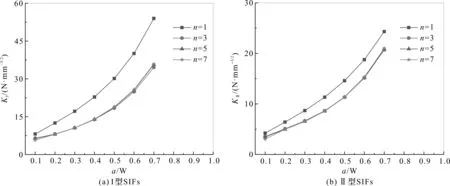
图8 裂纹数量变化时，边缘裂纹I，II型SIFs

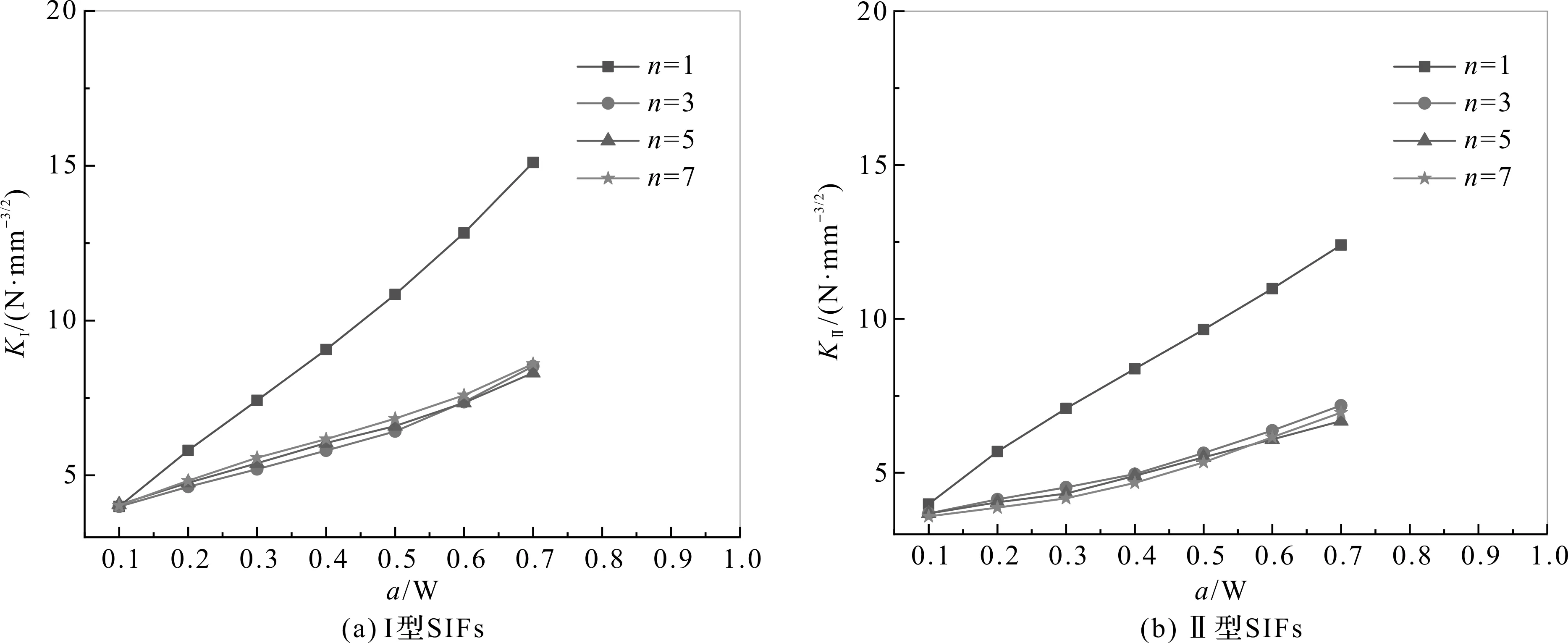
图9 裂纹数量变化时，中心裂纹I，II型SIFs

4 结束语

本文采用ABAQUS有限元分析软件模拟仿真人工心瓣热解炭涂层边缘裂纹和中心裂纹I-II复合型SIFs。仿真结果验证了有限元分析软件ABAQUS仿真模拟的合理性和可靠性。在裂纹倾斜角和裂纹长度改变时，I，II型SIFs均改变；在裂纹数量改变时，边缘裂纹和中心裂纹的I，II型SIFs曲线分别重合，且均小于单条裂纹情况下的I，II型SIFs。在此基础上，将对热解炭涂层疲劳裂纹扩展及使用寿命展开进一步研究。