一个经典Hilbert型积分不等式的推广
2020-12-03有名辉
有名辉
(浙江机电职业技术学院数学教研室,浙江 杭州 310053)
0 引 言
20世纪初,德国著名数学家Hilbert提出著名的Hilbert不等式[1]。时间已逾百年,世界各地的数学工作者对Hilbert不等式进行了深入且广泛的研究,取得了大量的离散型[2-5]以及积分型[6-9]的新成果。这些新成果往往形式美观,技巧多变,构造精巧,应用广泛,在分析学相关领域起着非常重要的作用。
对Hilbert型不等式的研究,一般可分为齐次和非齐次两种形态;还可研究核函数的参数化、离散化、半离散化以及不等式的高维推广、系数加强。在大量的已有文献中,研究者们往往侧重于核函数的系数和指数推广,而很少去改变核函数的结构。本文从一个新的角度构造一个多参数的积分核函数,并借助实分析的相关技巧,特别是余切函数的部分分式展开,建立一个新的Hilbert型不等式,推广相关经典的结果。
1 定义及引理
定义1设s>0,第二型欧拉积分定义如下:
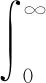
也称Γ函数[10]。特别地,当s∈N+时,Γ(s)=(s-1)!。
引理1设λ,γ>0,(2n+1)γ>β>0,n∈N,定义
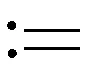
(1)
且有

(2)
则
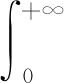
(3)
证明
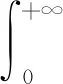
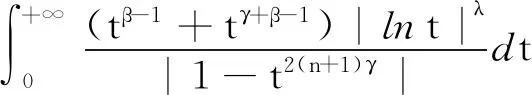
(4)
其中
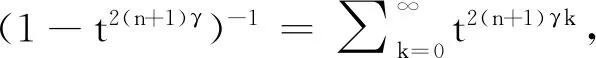
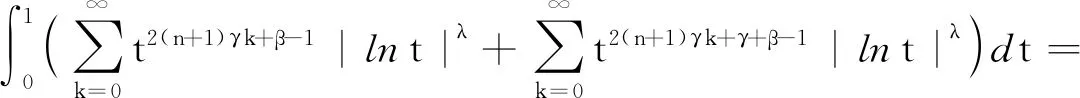
(5)
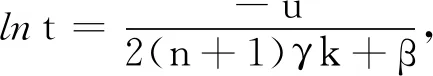
(6)
同理可得
(7)
把式(6)和式(7)代入式(5),得
(8)
令t=u-1,类似可得
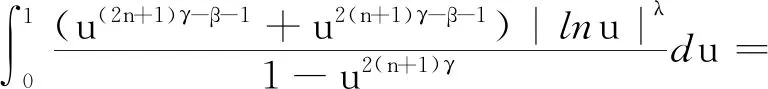
(9)
结合式(4)、式(8)以及式(9),并利用式(2),即得式(3)成立。引理1得证。
引理2设a,b>0,m∈N+,则
(10)
证明根据cotx的部分分式展开(参见文献[10]第397页):
(11)
式(11)两边关于x求2m-1阶导数,可得
(12)
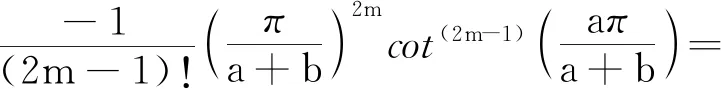
由此便得式(10)成立,引理2得证。
2 主要结果
若f,g≥0,f,g∈L2(+),通常有经典的Hilbert型不等式[1]:
(13)
以及
(14)
式中,π2是满足式(13)和式(14)的最佳常数因子。式(13)及式(14)的类比及推广可参见文献[11-13],在此构造新的积分核函数,将它们推广如下:
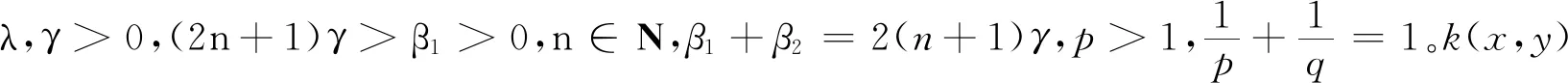
(15)
式中,C(γ,λ,β,n)是满足式(15)的最佳常数因子。
证明根据Hölder不等式,可得
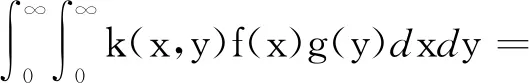
(16)
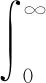
根据引理1可知,β1+β2=2(n+1)γ,不难算得
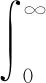
(17)
类似可得
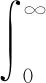
(18)
容易验证,在β1+β2=2(n+1)γ这一条件下,C(γ,λ,β1,n)=C(γ,λ,β2,n)。因此把式(17)和式(18)代入式(16),便有
(19)
假使式(19)中等号成立,那么一定有不全为零的实数A与B,满足
Axp(1-β1)fp(x)=C几乎处处在+成立,
及
Byq(1-β2)gq(y)=C几乎处处在+成立。
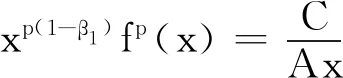
下面证明式(15)的常数因子为最佳值。若此常数因子不为最佳值,则定有实数0 (20) (21) 令ε→0+,并结合式(3),可得 (22) (23) 式中,C(γ,λ,β,n)是满足式(23)的最佳常数因子。 在定理1中,令λ=2m-1,m∈N+,n=0,利用引理2,注意到 则有 (24) 在定理1中,令λ=2m-1,m∈N+,n=1,利用引理2,则有 (25) 本文通过构造一个新的积分核函数,探究相应的Hilbert型二重积分不等式,推广了一些经典的结果。在最佳常数因子的处理方式上,借助余切函数的部分分式展开这一实分析的方法,解决了最佳系数用级数表达过于复杂的问题,具有一定的创新价值,对其他一些类似的Hilbert型积分不等式的研究具有一定的借鉴意义。
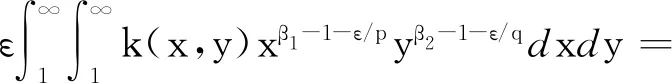
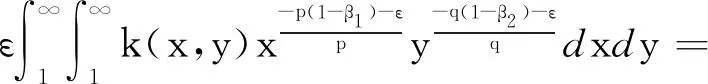

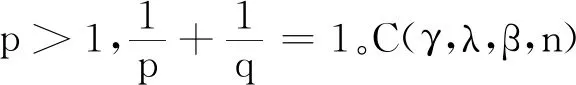
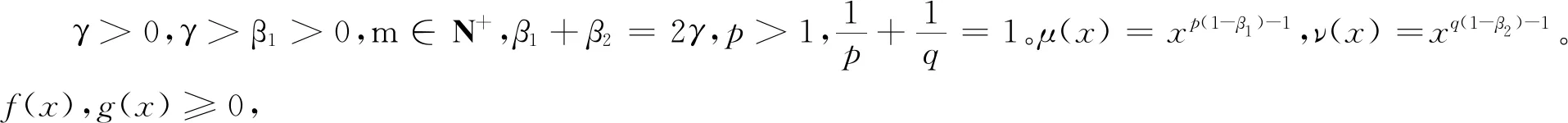
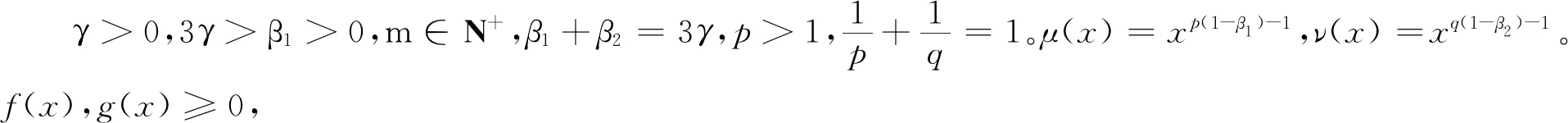
3 结束语
