具有随机时滞的区间时滞系统稳定性分析
2020-12-03刘丽丽姜偕富尹宗明郭娜娜
刘丽丽,姜偕富,尹宗明,郭娜娜
(杭州电子科技大学自动化学院,浙江 杭州 310018)
0 引 言
时滞现象普遍存在于网络控制、化工、生物等实际应用中,是造成系统性能下降或不稳定的主要原因之一[1]。因此,时滞系统的稳定性分析受到了众多学者的关注。过去的二十多年中,广大学者提出了许多研究时变时滞系统稳定性的方法,并取得了丰硕的研究成果[2-11]。例如,文献[3]研究具有区间时变时滞线性系统的稳定性问题,采用一阶、二阶零等式,取得较好结果,但计算较为复杂;文献[5-6]研究一类线性时滞系统的区间时滞相关稳定性问题,用Wirtinger积分不等式和凸组合的方法处理积分项,得到保守性较小的稳定性判据;文献[7]分析了时变时滞系统的稳定性问题,构造一种新的时滞乘积型L-K泛函,得到较好的结果。但是,上述文献只考虑时变时滞的变化范围和时滞变化率的信息,忽略了时滞的随机特性。事实上,时变时滞往往是随机的,如网络化控制系统中的诱导时滞。文献[9]研究了具有随机输入时滞的网络控制系统的稳定性及控制器设计问题,采用自由权矩阵处理积分交叉项,取得较好结果;文献[10]研究了具有随机输入时滞的网络控制系统的观测器控制问题,得到保守性较小的稳定性准则;文献[11]研究了具有随机时滞的多区间时滞系统稳定性问题,利用Finsler’s引理,得出较好的结果。然而,文献[9-10]中仅考虑时滞下界为零的情况,文献[11]只采用Jensen不等式和凸组合的方法来处理积分项,仍有较大的改进空间。本文研究一类具有随机时滞的区间时滞系统稳定性问题,构造一个新的增广型L-K泛函并充分利用时滞信息和区间时滞概率分布信息,给出保守性较小的稳定性准则。
1 系统模型
假设线性时变时滞系统模型如下:
(1)
式中,A,Ad为已知的具有适当维数的常矩阵;x(t)∈Rn为系统的状态向量;h(t)为系统的时滞函数且满足h1≤h(t)≤h3,h1和h3为已知标量;φ(t)为系统的初始值。
假设时滞h(t)在[h1,h2]和(h2,h3]上的概率分布是已知的。为了有效利用时滞的概率分布信息,定义如下2个随机事件:
Ω1∶h(t)∈[h1,h2], Ω2∶h(t)∈(h2,h3]
引入1个随机变量
定义2个函数h1∶R+→[h1,h2]和h2∶R+→(h2,h3],则有
不难发现,δ(t)服从伯努利分布,满足
Prob={δ(t)=1}=Prob{h1≤h(t)≤h2}=E{δ(t)}=δ,
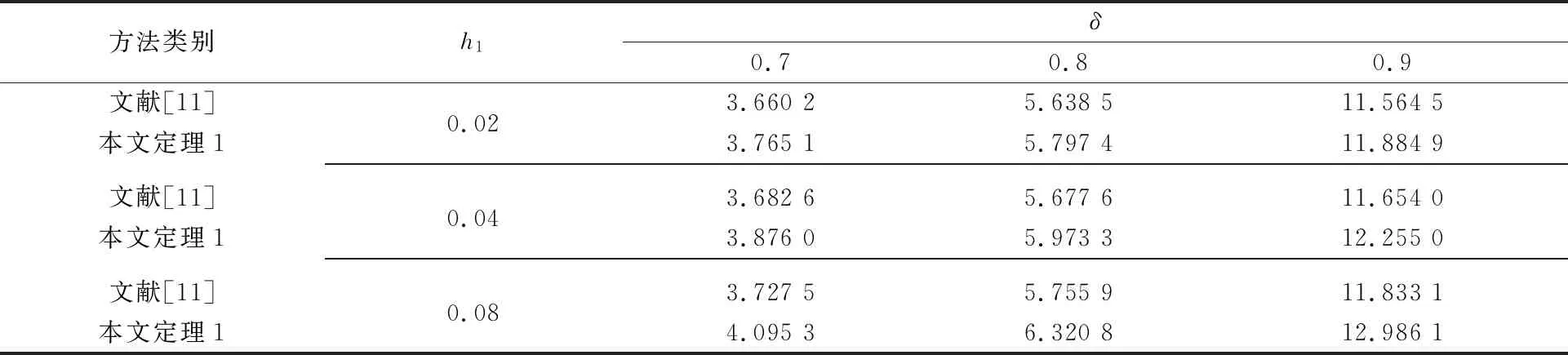
Prob={δ(t)=0}=Prob{h2 其中δ∈[0,1],δ和1-δ分别表示时滞h(t)在区间[h1,h2]和(h2,h3]上的概率。 综上,通过引入随机变量δ(t)和随机输入时变时滞h1(t)、h2(t)后,可以将系统(1)改写为: (2) (3) (4) (5) Ξ22=-Q1-R1-4R2,Ξ23=-2R2-U11-U12-U21-U22,Ξ24=U11-U12+U21-U22, h12=h2-h1,h23=h3-h2。 证明构造如下L-K泛函 V(xt)=V1(xt)+V2(xt)+V3(xt)+V4(xt) (6) 为了简化后续的推导过程,定义ξT(t)和ei分别如下: 沿系统轨迹(2)对V(xt)作无穷小算子 (7) 式中, (8) (9) (10) (11) 引入如下零等式 (12) 分别对式(10)中的R1相关积分项使用Jensen不等式处理,对R2和R3相关的积分项使用文献[4]中的引理2.1和文献[12]中的引理2处理,对式(11)中的Z相关的二重积分项使用文献[13]中的引理2处理,结合式(7)—(12),并对式(7)两端同时求期望可得: (13) 当Ξ<0成立时,存在1个足够小的常数λ>0,使得式(13)小于-λI,即 (14) 采用类似于文献[14]中的方法,对任意的t≥0,可得: (15) 使用MATLAB中的LMI工具箱求解定理1中线性矩阵不等式(3)—(5),求得所允许的最大时滞上界。选取2个数值示例来验证本文所得稳定性准则的有效性。 例1使用文献[5]中系统模型 分别采用文献[5]、文献[6]及本文方法求出所允许的最大时滞上界h3,结果如表1所示。 表1 不同的h1下,最大允许时滞上界h3 从表1可以看出:根据本文定理1得到的时滞上界比文献[5]、文献[6]中的大,虽然本文的决策变量数比文献[5]、文献[6]多,但是所得结果较好,说明本文所用方法最终得出的稳定性准则具有较小的保守性。 例2使用文献[11]中系统模型 时滞函数h(t)在2个区间上的概率分布是已知的。当h2=0.1时,对不同的h1和δ求得时滞上界h3,结果如表2所示。 表2 当h2=0.1时,不同的h1和δ下所允许的最大时滞上界h3 从表2可以看出:当时滞下界h1不变时,增大时滞在区间[h1,h2]上的概率δ,时滞上界h3随着概率增大而增大;当区间[h1,h2]上的时滞概率δ不变时,增大下界h1的值,时滞上界h3随着h1的增大而增大。通过与文献[11]中的推论1对比,在h1,h2,δ取值相同的情况下,本文得到的时滞上界较大,验证了本文采用方法的有效性。 通过上面2个例子可知:时滞上界h3的取值范围不仅与时滞下界大小有关,还与时滞概率δ分布有关。 本文针对一类具有随机时滞的区间时滞系统的稳定性问题进行研究。与以往文献不同的是,本文不仅考虑了时滞信息,还考虑了时滞在区间上的概率分布。研究结果表明,在充分考虑了时滞在区间上的概率分布情况下,得到的最大时滞上界比仅考虑时滞信息情况下的大,说明本文所得结果具有较小的保守性。但是,本文只考虑2个概率区间,下一步将对多个概率区间的时滞系统保守性问题展开研究。2 主要结果
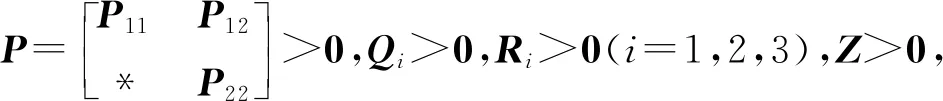
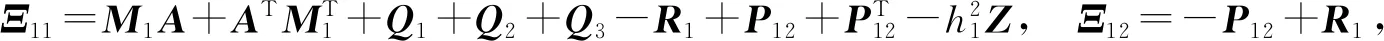
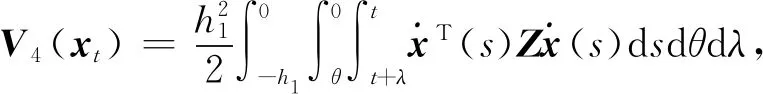
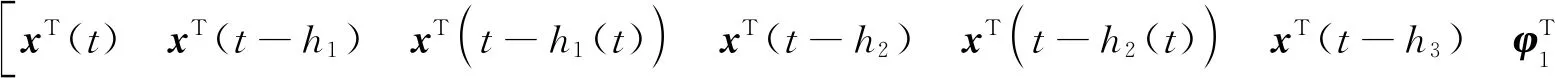
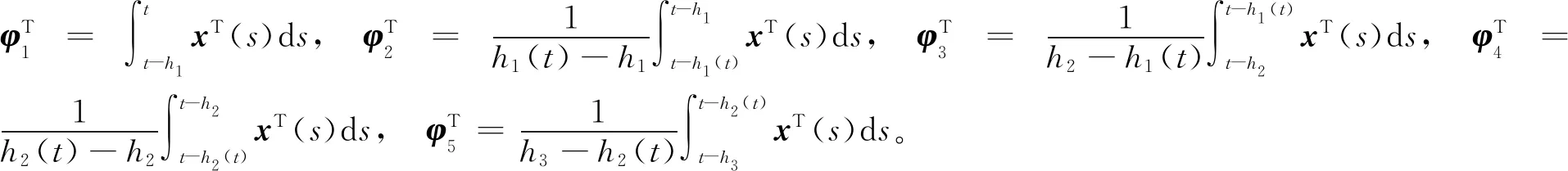
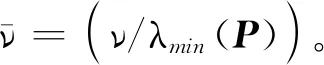
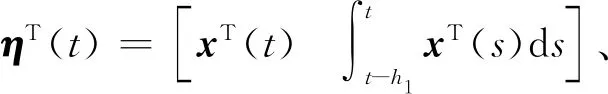
3 数值示例
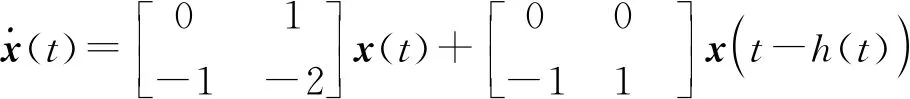

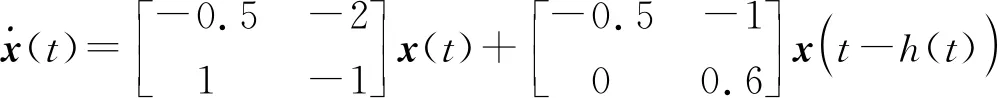
4 结束语
