金融风险法律论证中Copula理论的具体应用

摘 要 基于金融风险法律论证是一个非常复杂的问题，存在很多的不确定因素，且在以往的金融风险法律论证中计算过于复杂，实用性低。为此，提出Copula理论在金融风险法律论证中的应用研究。通过Copula理论跟踪金融风险法律论证信息，以此作為椭圆Copula中的正态Copula跟踪金融风险法律论证信息的依据，重构金融风险法律论证信息在路径中的分布;通过Copula理论判断金融风险法律论证指数变化，以金融风险法律论证指数波动性的映射函数与信号库映射的方式，推理金融风险法律论证指数的变化状态;通过Copula理论非线性度量金融风险法律论证分位数，在不研究边缘分布的情况下，非线性度量金融风险法律论证分位数分布相依结构;非参数核密度估计金融风险法律论证，实现Copula理论对金融风险法律论证的概率统计功能。

关键词 Copula理论 金融风险 法律论证 概率统计

基金项目：《数学方法在法律论证中的应用问题研究》省教育厅“十三五”社会科学项目（JJKH20201310SK）。

作者简介：张育梅，长春工业大学人文信息学院，副教授，研究方向：应用数学。

中图分类号：D922.28 文献标识码：A DOI：10.19387/j.cnki.1009-0592.2020.11.198

金融市场的自由化程度越来越高，所伴随的金融风险业务逐渐加深。金融风险指的是金融领域中受政治、社会心理以及经济所影响的意外倒闭现象，并且能够引发“多米诺骨牌”的危险。金融风险由于会受到很多因素的干扰，其中既包含政治因素，还包括经济因素。因此，一旦出现金融危机，大多数情况下都是金融风险指数爆发的结果。金融风险法律论证指的是对金融风险的推理、推论以及论证关系，在金融风险法律论证中，一般情况下可分为广义的金融风险法律论证以及狭义的金融风险法律论证。广义的金融风险法律论证指的是对金融风险进行立法论证与司法论证;而狭义的金融风险法律论证指的是在法律诉讼过程中对金融风险运用证据确定案件事实得出结论的思维过程。目前，我国针对金融风险法律论证方面的研究仍处于起步阶段，且在用于实际解决金融风险领域的问题中没有取得理想的效果，无法满足金融风险法律论证的现实需求[1]。在国外，针对金融风险法律论证方面的研究起步较早，并且取得了一定的研究成果，较为突出的是Copula理论在金融风险法律论证中的应用，通过Copula理论将多个金融风险分布函数进行灵活的多元分布，对金融风险法律论证建模流程进行简化，对金融风险法律论证进行精准分析。本文以此为借鉴依据，结合我国金融体系，进行Copula理论在金融风险法律论证中的应用研究，致力于通过Copula理论的合理应用，为金融风险法律论证方面的发展开创新局面。

一、跟踪金融风险法律论证信息

运用Copula理论中的椭圆Copula和Archimedean Copula，对金融风险法律论证信息进行跟踪[2]。基于金融风险的特点，假定金融风险法律论证信息可表示金融风险指数的实时具体数据，设金融风险指数离散信号的表达式为y，通过椭圆Copula中的正态Copula对其进行计算，其计算公式，如公式（1）所示。

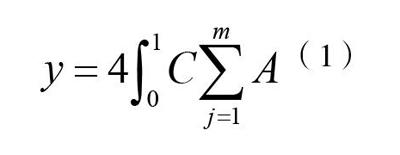
在公式（1）中：C指的是正态Copula;j指的是金融风险在严格法律论证变换下的不变性;j指的是金融风险法律论证信息个数，为实数;A指的是金融风险法律论证信息滤波转换次数序列分布平方和。根据上述计算公式，以此作为椭圆Copula中的正态Copula跟踪金融风险法律论证信息的依据，重构金融风险法律论证信息在路径中的分布。假定在跟踪金融风险法律论证信息过程中，金融风险法律论证信息的能量传输呈现逐步递减趋势，则可采用二元正态Copula理论表示金融风险法律论证信息。设二元正态Copula理论表示金融风险法律论证信息为E，则其计算公式，如公式（2）所示。

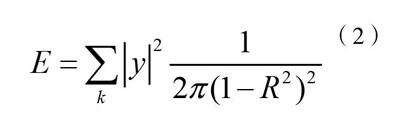
在公式（2）中：K指的是金融风险法律论证信息能量值;R指的是相关系数矩阵。根据公式（2），可较良好的表达Copula理论在金融风险法律论证信息跟踪方面的具体应用。

二、判断金融风险法律论证指数变化

根据金融风险法律论证信息的分布路径，判断金融风险法律论证指数变化，金融风险法律论证指数变化可通过金融风险法律论证指数的波动性进行表示[3]。利用Copula理论构建金融风险法律论证曲线，通过引入连续随机变量生存时间，从而得到金融风险法律论证指数波动性的计算公式。设金融风险法律论证指数波动性的计算公式为，则其计算公式，如公式（3）所示。

在公式（3）中：h指的是金融风险法律论证危险率;指的是金融风险法律论证的累积分布函数。通过公式（3）得出金融风险法律论证指数波动性数据的基础上，用正态Copula理论连接单变量分布函数，以金融风险法律论证指数波动性的映射函数与信号库映射的方式，推理金融风险法律论证指数的变化状态[4]。通常情况下，金融风险法律论证指数在终端的映射取值在0～1.0之间，通过计算每个金融风险法律论证指数的映射值，以此判断金融风险法律论证指数变化情况。设判断金融风险法律论证指数变化的表达式为w，则其计算公式，如公式（4）所示。

在公式（4）中：K指的是金融风险法律论证指数波动幅值;指的是金融风险法律论证指数变化识别框。通过公式（4）计算得出的映射值作为判断金融风险法律论证指数变化的关键依据，结合我国金融体系的实时情况，更好的指导金融风险法律论证。

三、非线性度量金融风险法律论证分位数

考虑到金融风险法律论证在本质上就是非线性问题，因此，本文通过Copula理论将金融风险法律论证中的风险进行分解[5]。例如，可以基于Copula理论灵活多元分布的特点，将一个金融风险中所包含的风险，分为若干个子风险，也可以称之为金融风险法律论证的分位数。由于Copula理论对于随机变量的严格单调变换是不变的，可以通过Copula理论对金融风险法律论证分位数进行非线性度量，进而清楚地反映出金融风险法律论证的层次结构。设某金融风险中共包含n个层次，将n个层次的金融风险看作一个整体板块，设整体板块为a，且a包含若干个Copula理论，则可以利用若干个Copula理论以非线性的方式对a中的分位数进行度量。以Copula理论的相依结构，从概率的角度来反映金融风险法律论证分位数间的相关程度。设非线性度量金融风险法律论证分位数的Copula理论表达式为，则其计算公式，如公式（5）所示。

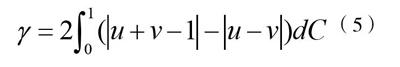
在公式（5）中：u指的是金融风险法律论证分位数相反变化的不一致程度;v指的是金融风险法律论证分位数总的不一致性;d指的是金融风险法律论证分位数之间的关联系数。通过公式（5），可以求出金融风险法律论证分位数非线性的相依测度，进而实现利用Copula理论对金融风险法律论证分位数进行非线性度量。在此过程中，需要注意的是必须通过Copula理论的正态Copula以及负态-Copula确定金融风险法律论证分位数的边缘分布;并是选取一个与之匹配度最高的Copula理论以描述金融风险法律论证分位数边缘分布之间的相依结构。除此之外，通过边缘分布和Copula理论可以确定金融风险法律论证信息的条件联合分布函数，进而计算出条件均值、方差及高阶协矩等统计量作为金融风险法律论证的测度。以此，为非线性度量金融风险法律论证分位数提供了一个便捷的方法，能够在不研究边缘分布的情况下，非线性度量金融风险法律论证分位数分布相依结构。

四、非参数核密度估计金融风险法律论证

Copula理论在金融风险法律论证中应用的最出色之处在于将Copula理论中的概率估计能力应用在金融风险法律论证中，进而为金融风险法律论证提供概率参照。应用Copula理论非参数核密度估计金融风险法律论证的具体流程为：首先，设金融风险法律论证随机变量为X;金融风险法律论证相依结构为Y，则有金融风险法律论证随机变量的非参数核密度函数为g（X），金融风险法律论证相依结构的非参数核密度函数为g（Y）。而后，基于Copula理论建立金融风险法律论证非参数核密度估计的高阶协矩，g（X）非参数核密度估计的高阶协矩，如公式（6）所示。

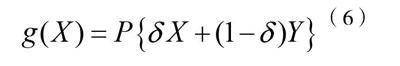
在公式（6）中，P指的是非參数核密度估计金融风险法律论证的置信水平;指的是非参数核密度估计金融风险法律论证的方差。再利用公式（6）得出金融风险法律论证随机变量的非参数核密度估计的高阶协矩后，可推导出g（Y）非参数核密度估计高阶协矩的计算方程式，如公式（7）所示。

在公式（7）中，指的是资产组合生存时间的联合概率。通过上述公式，可以实现基于Copula理论非参数核密度估计金融风险法律论证。综上所述，可以看出Copula理论在金融风险法律论证中的应用主要在于对金融风险法律论证分析领域中，且具有对金融风险法律论证的概率统计功能。

五、结语

通过Copula理论在金融风险法律论证中的应用研究，不难发现Copula理论可以帮助金融风险法律论证更好的发展。尽管本文考虑到篇幅问题，没有对本文提出的Copula理论在金融风险法律论证中的应用进行实例分析，但结合以往研究表明以及本文得出的结论，能够证明Copula理论在金融风险法律论证中应用的可行性。因此，有必要加大Copula理论在金融风险法律论证中的应用力度，以Copula理论为核心，为金融风险法律论证提供更加广阔的发展空间。

参考文献：

[1] 韩菲，王超.中国经济政策不确定性与亚洲股市的动态关系——基于时变Copula模型的分析[J].投资研究，2018，37（7）：103-114.

[2] 杨佳玫.基于机制转换混合copula的金融市场风险传染效应研究[J].现代商业，2018，1（35）：110-113.

[3] 王佳，杨艾琳，王旭.基于修正KMV-Copula模型的组合信用风险度量研究[J].会计之友，2019，1（7）：53-58.

[4] 柴尚蕾.周鹏.基于非参数Copula-CVaR模型的碳金融市场集成风险测度[J].中国管理科学，2019，27（8）：1-13.

[5] 陈倩.梁力军.基于分段损失分布法和Copula的银行操作风险集成度量[J].运筹与管理，2019，28（8）：174-181.