An SPH wave-current flume using open boundary conditions ＊

Xing-ye Ni , Wei-bing Feng, Shi-chang Huang Zi-jun Hu Yong Liu

1. Zhejiang Institute of Hydraulics and Estuary, Hangzhou 310020, China

2. College of Harbor, Coastal and Offshore Engineering, Hohai University, Nanjing 210098, China

Abstract: In this paper, a novel numerical wave-current flume is implemented based on the smoothed particle hydrodynamics (SPH)method.The proposed flume is more stable and computationally efficient than conventional ones because it cancels wave paddles or sponge layers while using a non-reflective open boundary condition to simultaneously generate and absorb waves and currents.Numerical tests of nonlinear regular waves interacting with steady currents in the same/opposite directions indicate that the wave-current interactions mainly affect the horizontal velocity distributions in the water body, with little influence on the vertical movements.Water particle trajectories are stretched, and the mass transportation effects are enhanced when the waves and currents are in the same direction.When the directions are opposed, the trajectories, as well as the mass transportation, are compressed,suppressed and even reversed.The applications of solitary wave-current interaction over a submerged bump further show that the relative direction between the wave and the current has remarkable influence on the wave breaking pattern over an underwater obstacle.

Key words: Smoothed particle hydrodynamics (SPH), wave-current interaction, wave-current flume, open boundary condition,particle trajectory

Introduction

Waves and currents generally coexist under natural conditions.Comparing the wave-alone or current-alone conditions, the wave-current interactions reveal new features about water body movements,raising new challenges for the study of coastal hydrodynamics.Analytical methods[1]and experimental studies[2]are two major approaches to conventional wave-current research.With the development of computer technologies and numerical simulation methods, the numerical wave-current flume (NWCF) has recently become a major tool for wave research.Navier-Stokes equations are generally used to govern the NWCF, most of which are discretized by mesh-based numerical methods, e.g.,the finite difference method (FDM)[3]and finite volume method (FVM)[4-5].Specific algorithms, e.g.,the volume of fluid (VOF) and level-set method(LSM), are required to capture free water surfaces,which can be time-consuming and tricky to implement.Moreover, mesh distortions occur in highly nonlinear hydrodynamic conditions, e.g., water interactions with complex structures, wave breaking and plunging,leading to large numerical errors and even model blow-up.Mesh-based models also have difficulties handling moving boundaries in cases of fluid-solid interaction.

Mesh free numerical methods have recently been applied to small-scale hydrodynamic simulations.smoothed particle hydrodynamics (SPH) is one of the most promising methods.The SPH method was first proposed early in 1977 independently by Gingold and Monaghan and Lucy to solve astrophysics problems in three-dimensional open space.The system is discretized using a large number of particles, i.e.,computational nodes, each of which represents a small medium of the subjects.There are no direct grid connections between these particles, preventing the mesh distortion problems in conventional models and making the SPH method suitable for the simulation of highly nonlinear hydrodynamic cases[6-7]that consist of complex free surfaces and solid boundaries.

Since Monaghan first applied the SPH method to model physical wave paddles that generate waves and simulated wave run-up on a slope, progress has been made regarding wave generation theories[8-10]and the practical applications[11-13]of the SPH numerical wave flumes (NWFs).Conventional SPH NWFs[8]use wave paddles to generate waves and numerical sponge layers to absorb waves, as shown in Fig.1(a).Internal wave makers, which were based on the momentum theory and were originally used in mesh-based NWFs,were also utilized to generate regular waves[14]and irregular waves[15]in SPH NWFs, as shown in Fig.1(b).Lo and Shao[16]proposed another wave generation technique to make solitary waves using a prescribed wave profile based on wave kinematics.

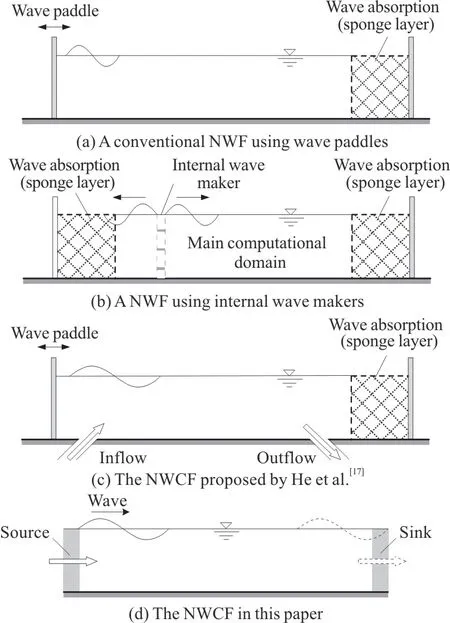
Fig.1 Sketch of various types of SPH numerical wave flumes and wave-current flumes

Considering the Lagrangian features of the SPH method, certain numerical issues need to be addressed when introducing mass sources into the system.To date, there have been very few studies on the implementation of SPH NWCFs as well as few studies on wave-current interactions using the SPH method.He et al.[17]proposed an SPH NWCF, which was similar to the wave-current flumes used in the laboratory, by deploying an inflow pipe on the bed in front of the paddles while deploying an outflow pipe in front of the sponge layer, see Fig.1(c).These authors also used the SPH NWCF to simulate interactions between regular waves and steady currents in the same direction.As a velocity oscillation is triggered in the flume after initiation of the simulation, resulting from the U-tube effects between the inflow and outflow pipes, a temporary rigid-lid treatment is applied to the water surface to reduce the time to reach a steady state.However, local flows are distorted, since the directions of the inflow and outflow from the bed are not parallel to the direction of wave propagation, leading to unpredictable consequences for numerical simulations.

Based on non-reflective open boundary conditions, Ni et al.[10]recently proposed a novel SPH NWF (Fig.1(d)), which is capable of generating and absorbing various waves, including solitary waves,regular waves and irregular waves.Since the solid wave paddle and the sponge layer are no longer required, this type of SPH NWF not only shows advantages of computational efficiency over conventional methods but also provides new possibilities for the implementation of SPH NWCFs.

In this paper, a novel SPH NWCF is presented based on the work of Ni et al.[10], and it is applied to study the hydrodynamic features of various wavecurrent interaction cases.The paper is structured as follows.The background of SPH NWCFs is reviewed in Section One.The mathematics of the SPH method and the SPH hydrodynamic model are briefly introduced in Section Two.Section Three presents the implementation and the validation of our SPH NWCF.Section Four uses the Lagrangian features of the SPH model to study the velocity distributions and the characteristics of water particle trajectories from regular wave interactions with steady currents in various cases.The proposed SPH NWCF is applied in Section Five to simulate solitary wave-current interactions over a bump in various current conditions.Sections Six and Seven present the conclusions and acknowledgements, respectively.

1.SPH model

The core concept of the SPH method is system discretization using a limited number of particles,which not only represent direct material properties,e.g., density, velocity and pressure, but also act as computational nodes.The field functionf(r) (see Eq.(1)) and its derivative ∇·f(r) (see Eq.(2)) at any position in the system can be calculated by accumulating all the neighboring particles according to a weighting function, otherwise known as a smoothing function or kernel function.Readers are referred to the works of Liu and Liu[18]for a more detailed theoretical discussion and formulation.

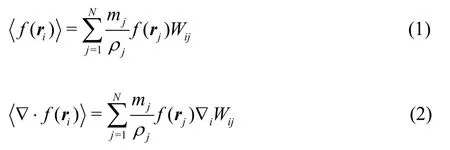
wherefrepresents any field function in the system.The subscriptsiandjindicate the central particle and a neighboring particle, respectively.The variablesmandρdenote the mass and density, respectively,of the particle.The smoothing functionWij=W(ri-rj,h) describes the weighting influence of particlejon particlei, andhis the smoothing length.

The momentum equation and the continuity equation of Navier-Stokes equations can be written in a Lagrangian form:

whereu,ρandPindicate velocity, density and pressure, respectively.Additionally,gis the gravity acceleration,Γis the dissipative term.In this paper,a Large Eddy Simulation model for the SPH method,i.e., the sub-particle scale (SPS) model, is adopted to simulate the turbulence, following the work of Gotoh et al.[19].

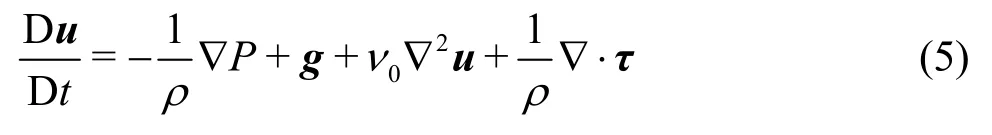
where the third term and the fourth term on the right-hand side of the equation are the force arising from the laminar and turbulence viscosity.Additionally,ν0is kinetic viscosity,τis the SPS stress tensor with

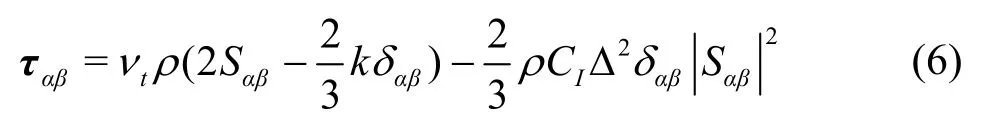
wherekis the SPS turbulence kinetic energy, the turbulent eddy viscosity, and the Smagorinsky constantCs=0.12,CI=0.0066,δαβ=｛1α=β,0α=β｝and.Δ is the particle initial interval,Sαβis the element of SPS strain tensor written as

Thus, Eq.(5) is written into the SPH form

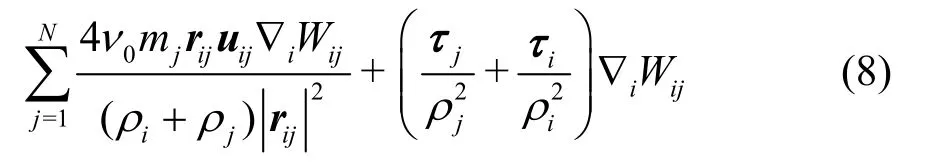
The weakly compressible SPH (WCSPH) method,which treats water as weakly compressible fluid, is used in this paper as the main framework model.Theδ-SPH formulas[20-21]are applied to calculate the density change rate of fluid particles:

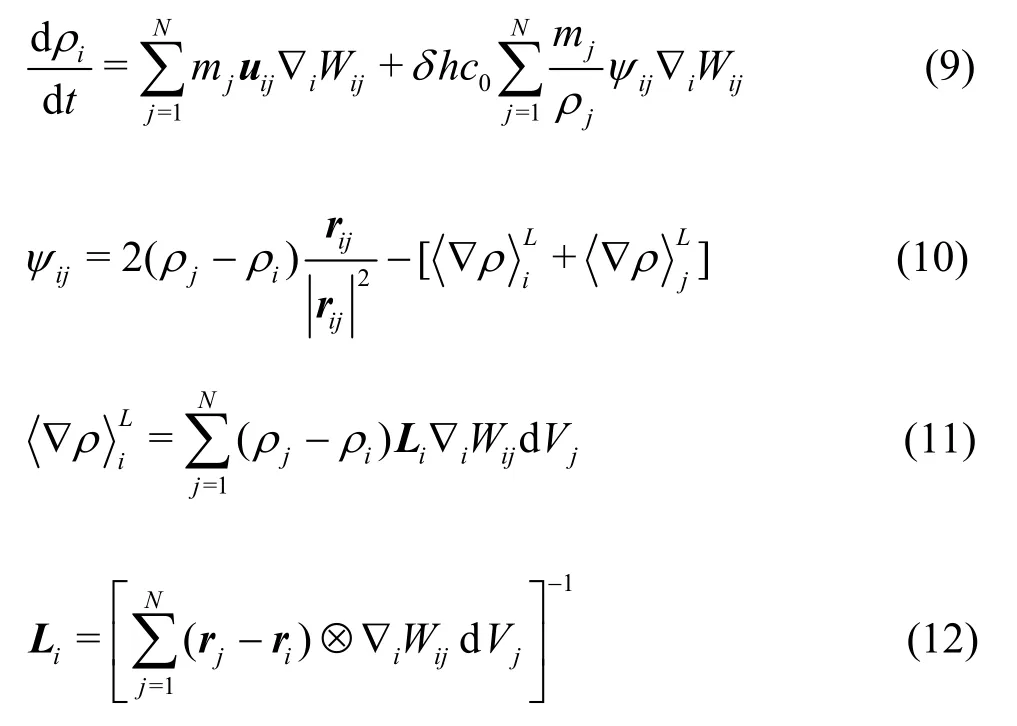
where the second term on the right-hand side of Eq.(9)is the dissipative term for the density change rate.This term will relieve the nonphysical oscillation of density and pressure in WCSPH, whereδcontrols the dissipative intensity of density change rate.The valueδ=0.1 is used in this paper.

Meanwhile, the fluid pressure is explicitly linked with its density based on the concept of artificial compressibility.Then, the pressure is obtained through the equation of state as

whereγ=7,.ρ0in dicates the reference density andρ0=1000kg/m3is the water simulation.c0is the artificial speed of sound, which is usually chosen to be larger than 10 times the fluid velocity to maintain the variation range of fluid density within 1%.

2.A wave-current flume and validation

2.1 An SPH wave-current flume using open boundary conditions

Based on the techniques of non-reflective open boundary conditions[10,22]for meshfree models, the SPH NWCF proposed in this paper simultaneously generates targeted waves and currents by managing the water depths and velocity of the open boundaries through prescribed signals and adding/deleting fluid particles in real time.As shown in Fig.1(d), a wave-current source is deployed on the left end of the flume to input both waves and currents, the directions of which can be either the same or the opposite.The source can also absorb the reflected waves from the structures in the flume, known as the function of active wave absorption (AWA).On the right end of the flume, there is a wave-current sink, which is capable of transporting both energy and matter out of the system without any reflection.The open boundary condition used in this paper is implemented using a buffer zone, the numerical details of which can be found in the work of Ni et al.[10].

2.1.1Wave-current generation

The water depthdBand the particle velocity(u,w) inside the wave-current source are prescribed as follows:

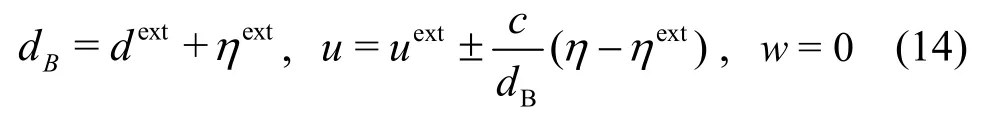
whereηdenotes the wave elevation near the open boundary,dextandηextdenote the external signals of water flow depth and wave elevation, respectively.dextequals the time-averaged water depth for the currents, with small variations in water depth.cis the phase speed of the water surface perturbations.Considering the Doppler effect of water-current interactions, the phase speed is given according to the relative direction between waves and currents

The particle velocityuextand the surface perturbationηextare not directly assigned by the analytical solution of the targeted waves.Instead, the first-order and second-order regular waves in this paper are driven by a set of depth-averaged signals following the work of Ni et al.[10]as follows:

whereH,kandωdenote the wave height, wave number and circular frequency, respectively.W#is the hydraulic transfer function.

2.1.2Wave-current absorption

The vertical velocity of fluid particleiin the wave-current sink iswi=0, while the horizontal velocityuifor regular wave-current interactions is given as

wheredenotes the depth-averaged velocity given by Flather’s open boundary condition (FOBC).f(zi)is the ratio between the particle velocity and the depth-averaged velocity according to the first-order Stokes wave theory.andf(zi) are given by Eqs.(20), (21), respectively.

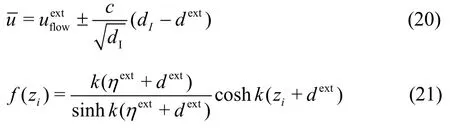
wheredIdenotes the water depth near the open boundary,ziis the vertical coordinate of particleiin the open boundary.

The water depth at the wave-current sink is calculated by the radiation equation

2.2 Regular wave interactions with steady flows

The wave-current interaction experiments conducted by Umeyama[2]are used in this study to validate our SPH NWCF.The steady current velocity in the flume is 0.080 m/s, with a water depth of 0.300 m.The regular wave with the same direction has a wave height of 0.023 m and a wave period of 1.00 s.The computational resolution is 0.005 m.Figure 2 presents the free surface evolutions in both the wave-alone case and the wave-current case.

Fig.2 (Color online) Evolutions of water surface elevation in the wave-alone case and the wave-current case

The numerical results, which agree with the experimental data satisfactorily, show that the wave amplitude decreases when a current is introduced to the wave motion.The wave-current case is also simulated with the resolutions of 0.007 m and 0.010 m and satisfactory numerical convergence is observed.

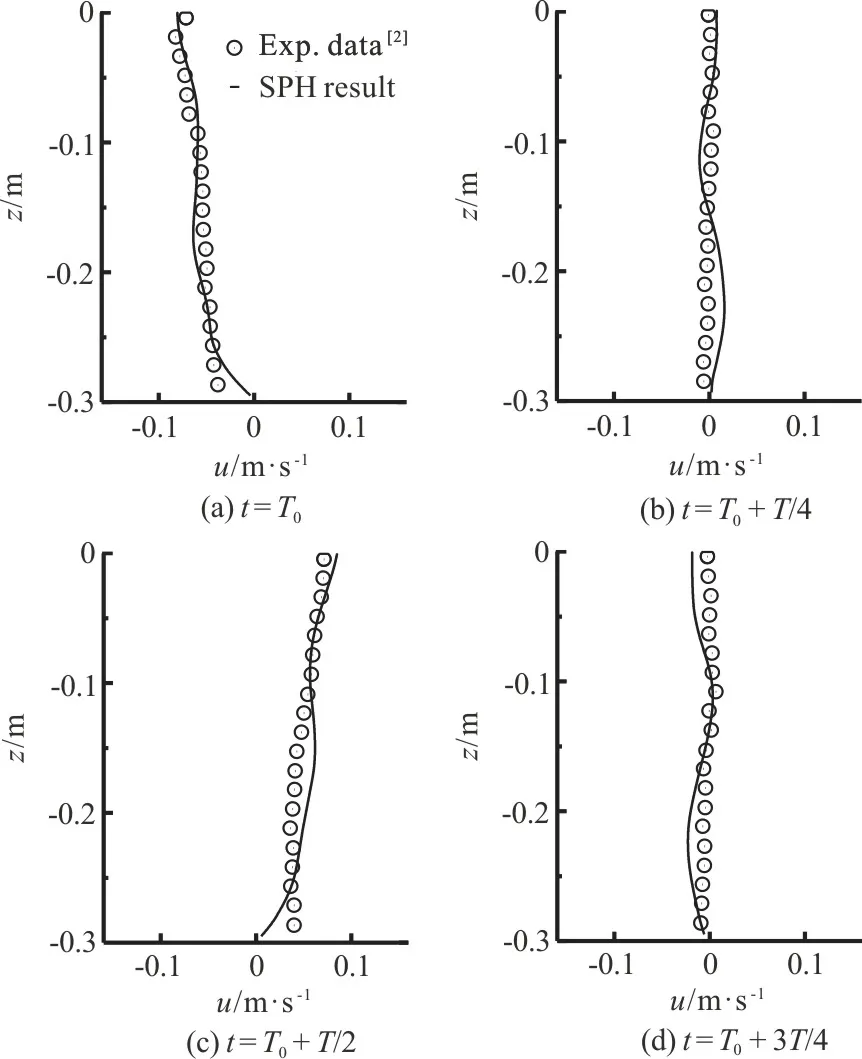
Fig.3 Horizontal velocity distributions in the wave-alone case

Fig.4 Horizontal velocity distributions in the wave-current case

Figures 3, 4 give the distributions of horizontal velocities in the vertical direction in the wave-alone and wave-current cases, respectively.If only propagating waves are present, the water particles are driven to oscillate, and the directions of flow velocity switch periodically, see Fig.3.However, the waveinduced velocities are suppressed by the steady current in the wave-current case, as shown in Fig.4.The flow velocities only vary in value without any change in direction.These hydrodynamic features given by the SPH model match the experimental data,indicating that the proposed NWCF is capable of simulating the interaction process between regular waves and steady flows.

3.Nonlinear hydrodynamic features of regular wavecurrent interactions

With the reduction of the relative water depths and the increase in the relative wave heights in nearshore areas, the water surface nonlinearity increases gradually.The water particle trajectories are no longer closed, presenting the phenomenon known as Stokes drift, which induces mass transportation in the wave direction.New hydrodynamic features occur in the water body when the nonlinear waves interact with nearshore currents, bringing complexity to the coastal sediment scour and transportation.Considering the intrinsic Lagrangian features of the SPH method, which makes it possible to track the particle trajectories automatically, the proposed SPH NWCF applied in this section explores the hydrodynamic features of nonlinear waves in currents with the same/opposite directions.

Fig.5 The water particle velocity distributions and trajectories in the wave-current interaction fields

A steady current withu=0.100 m/s is added to a regular wave field with a water depthd=0.400 m ,wave periodT=1.45s , and wave heightH=0.100 m in the same or opposite direction.The current velocity value was selected to prevent the suppression effect on the wave motion.Figure 5(a1)presents the water particle velocity distributions in a wave-alone case, which match the analytical description of regular waves.The water particles at the wave peak sections move horizontally in the same direction as the wave propagation, while those at the wave trough move in the opposite direction.The water particles close to the mean water level generally move in the vertical direction.The velocities of the near-surface water particles are much higher than those near the bed, particularly the vertical velocities

Figure 5(a2) shows the water particle trajectories in two and a half wave periods.The water particles near the bed move in a circular manner in closed flat trajectories, while those near the surface move in open elliptical trajectories, which are characteristic of nonlinear waves.It is also easy to tell that the near-surface water body is the primary contributor to mass transportation in the nonlinear wave propagation.

When the propagating waves interact with a steady current (u=0.100 m/s)in the opposite direction, the forward motions of the water particles at the wave peak section are suppressed, as shown in Fig.5(b1), while the backward movements at the wave trough section are enhanced remarkably.Fig.5(b2)shows that the forward trajectories are compressed,and the backward ones are stretched, indicating that the mass transportation caused by the nonlinear wave propagation is counteracted or reversed by the steady current.In contrast, the flow has little influence on the vertical motions, similar to the pure wave case.

When the propagating waves interact with a steady current (u=0.100 m/s)in the same direction,the forward velocities of the water particles at the wave peak section are further increased, and the backward velocities are reduced, while the vertical velocities undergo little change, as shown in Fig.5(c1).The net speed of a water particle in the mass transportation near the free surface is 0.159 m/s under these conditions, suggesting that the steady current contributes almost 74% of the water motion,comparing with 0.041 m/s in wave-alone case.The velocity distribution pattern continues to be affected by the nonlinear wave, as shown in Fig.5(c2).

It can be speculated that, if the flow velocity increases, then the backward motion of water particles will be fully suppressed, and the trajectories will exhibit a trochoid pattern.On the macro level, the wavelength will increase when interacting with flows in the same direction and will decrease when interacting with flows in the opposite direction, in accordance with the Doppler effect.

4.Solitary wave-current interaction over a bump

Currents not only change the water particle trajectories and the velocity distributions in waves, but also affect the hydrodynamic features of wavestructure interactions.In this section, the proposed SPH NWCF is applied to simulate the solitary wave propagation over a submerged bump in various current conditions and preliminarily study the features of current-wave-structure interaction.

A frictionless channel with a length of 10.000 m is adopted and the bed elevation is defined by Eq.(23),where the maximum height of the bumpb0=0.300 m.The test case of steady flow over a bump[22]is widely used to verify the numerical model capability of handling inflows/outflows, nonlinear terrains and shock waves.Thus, in the first test case of this section, i.e., case A, the water depths and the current velocities at the upstream/downstream open boundaries are 0.400 m and 0.125 m/s, respectively.The steady current speeds up and the water level reduces on the top of the bump due to the Bernoulli’s principle.The velocity and the water surface recover after the current surmounts over the bump.The analytical solution[23]of case A can be obtained by Eq.(24).

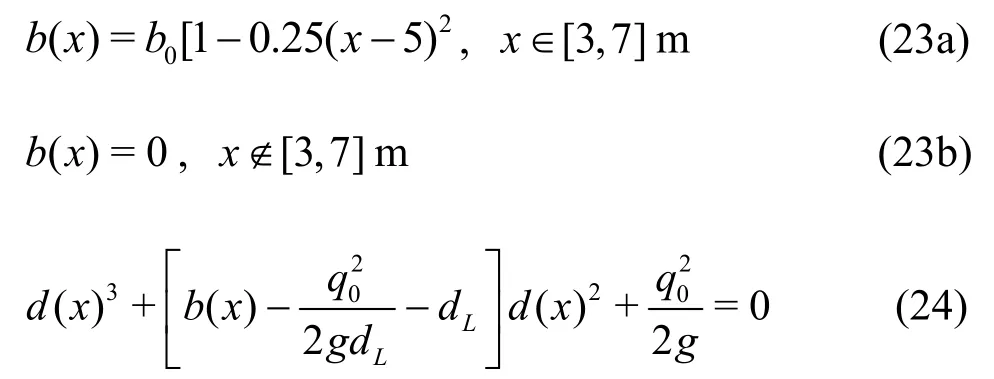
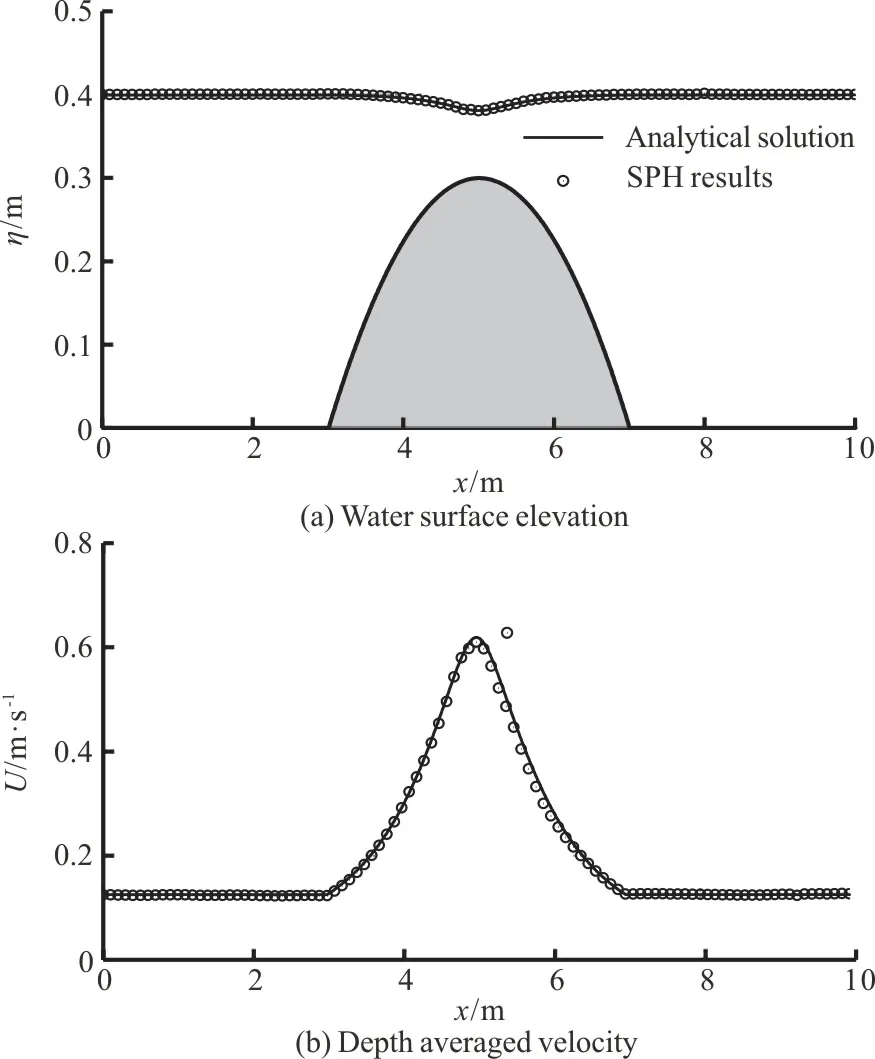
Fig.6 Steady flow over a bump

wherex∈ [0,L] ,dL=0.400 m.The channel lengthL=10.000 m and the current fluxq0=0.05m2/s.The computational resolution is 0.010 m in all the test cases of this section.Figure 6 gives the water surface elevation and the depth-averaged velocity along the channel and the numerical results match the analytical solutions satisfactorily with the relative error of 0.17% and 1.46%, respectively,considering that there are approximately 10 particles(computational nodes) on the top of the bump.

The velocity distributions of case A are presented in Fig.7, further indicating that our SPH model is capable of accurately predicting the interaction between steady flow and uneven terrains.

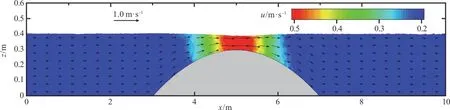
Fig.7 (color online) Solitary wave-current interaction over a bump: Currents alone

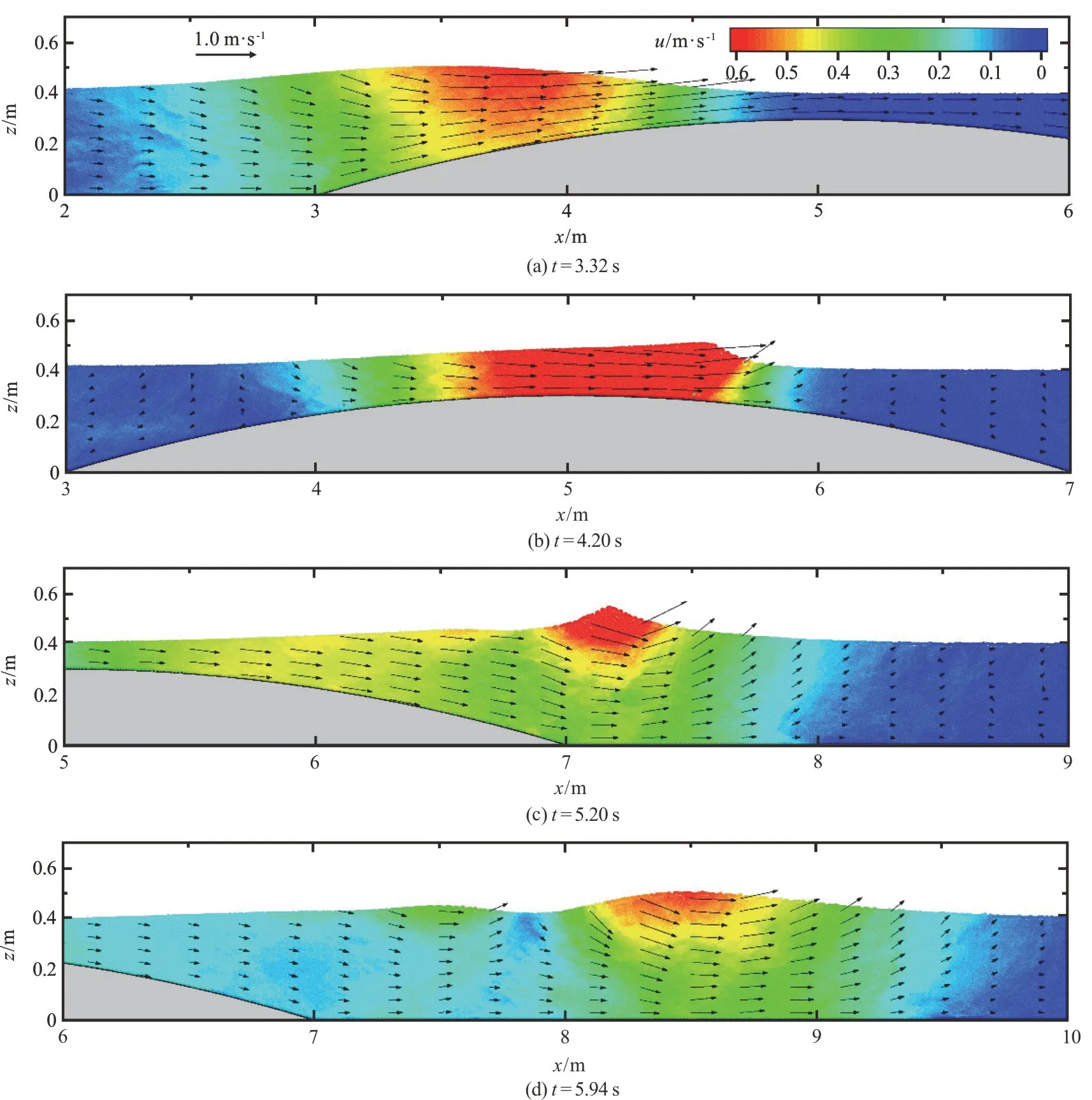
Fig.8 (color online) Solitary wave-current interaction over a bump: Solitary wave alone

The solitary wave propagations over a bump in steady water, in currents with the same direction and the opposite direction are simulated in cases B, C and D, respectively.The solitary wave height is 0.100 m.The parameters of the terrains and the current remain the same as those in case A.The wave profile and velocity distribution evolutions of the solitary wave-bump interaction in steady water are presented in Fig.8.When the solitary wave propagates onto the bump, the wave steepness increases and the wave profile leans forward gradually due to the shallow water effect (t=4.20s).However, the solitary wave does not break in this case.The wave crest turns into a sharp shape after propagating over the bump and this is when the wave height reaches its maximum value att=5.20s.Then secondary waves are gen erated a nd propagate forward with the main wave, asshownin Fig.8 att=5.94s.The phenomenon of solitary wave fissions induced by submerged obstacles was also simulated and discussed in the work of Li et al.[24].

As shown in Fig.9, the solitary wave propagates in the same direction as the current, which enlarges the solitary wave length and enhances its capability of surmounting a submerged obstacle.The distance between the main wave and the secondary wave is also larger than that in the wave-alone case.In contrast, the solitary wave height grows so quickly that it breaks on the bump due to the wave-current collision when they are in the opposite direction, as shown in Fig.10.The breaking patterns of solitary waves on the bump (t=4.40 s) together with the reflected jets and the spindrifts, are well simulated by the SPH model, indicating the promising advantages of SPH method on handling highly nonlinear hydro-dynamic problems and capturing fractured water surfaces.Since part of the potential energy is dissipated during the wave breaking, the solitary waves leaving the bump obtain smaller wave heights than those in the nonbreaking cases (cases B, C).Figure 11 gives the solitary wave height evolutions along the channel in various current conditions and the trends match the aforementioned descriptions.

Fig.9 (color online) Solitary wave-current interaction over a bump: Waves and currents in the same direction

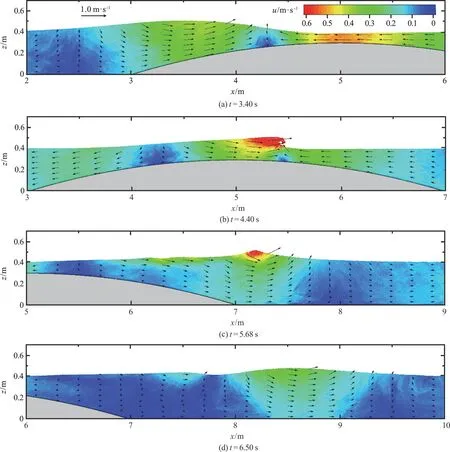
Fig.10 (color online) Solitary wave-current interaction over a bump: Waves and currents in the opposite direction

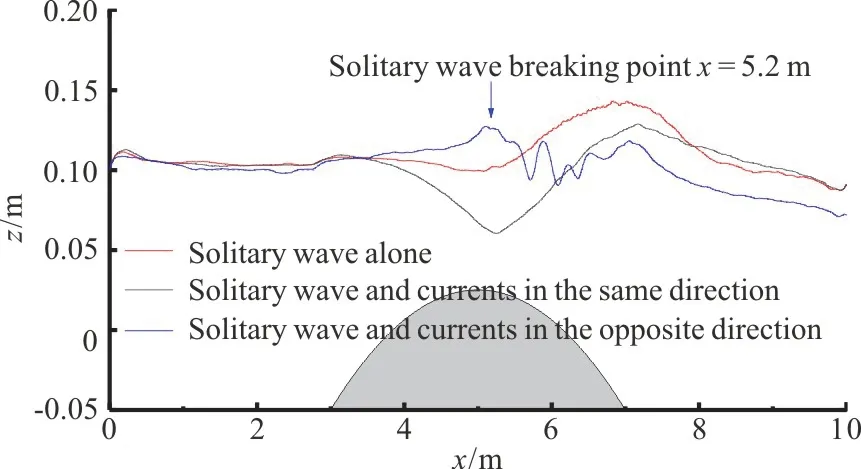
Fig.11 (color online) Solitary wave height evolutions along the channel

The proposed SPH NWCF generally gives satisfactory simulations of solitary wave-currentbump interactions and well predicts multiple complex nonlinear hydrodynamic phenomena, e.g., solitary wave shoaling, breaking and fissions.In the study of coastal hydrodynamic processes, the solitary wave is commonly used to describe the tsunami propagation pattern in nearshore waters, while the terrain with a bump is similar to the longshore sandbars or the submerged breakwaters.Thus, the study cases in this section can be further applied to investigate the tsunami-submerged breakwater interactions during various tidal periods.If the tsunami propagates over a submerged breakwater with an ebb tide, there is a larger probability that the tsunami wave breaks on the obstacles and the shock to the coast is then reduced.If there is a flood tide during the tsunami propagation,the tidal current will help tsunami surmount the submerged obstacles.Additionally, the tsunami wave will be fissured over the submerged obstacles, leading to a tsunami wave group with a smaller maximum wave height but a longer impacting period.

5.Conclusions

In this paper, a novel numerical wave-current flume is implemented based on the SPH method using a non-reflective open boundary condition.This SPH NWCF is capable of generating and absorbing waves and currents simultaneously without any of the wave paddles or sponge layers used in conventional flumes,making it more stable and computationally efficient.The processes of regular waves interacting with steady currents, including the water surface evolutions and velocity distributions, are reproduced well in this study when compared with the experimental data in the literature.

Numerical tests of nonlinear regular waves interacting with steady currents in the same/opposite directions indicate that the wave-current interactions primarily influence the horizontal velocity distributions in the water body and have less effect on the vertical movements.Water particle trajectories are stretched, and the mass transportation effects are enhanced when the waves and currents are in the same direction.Furthermore, water particle trajectories are compressed and suppressed when the waves and currents are in the opposite direction.The mass transportation due to nonlinear waves can even be reversed by the currents.In the macro perspective, the Doppler effect of wave-current interactions manifests as the stretch or the compression of the water wave lengths.The applications of solitary wave-current interaction over a submerged bump further verify the Doppler effect and indicate that the relative direction between the wave and the current has remarkable influence on the wave breaking pattern over an underwater obstacle.

It should be noted that the current NWCF in this paper is not suitable for the generation of waves with wave heights smaller than the computational resolution.This is also the perplexing limitation of other SPH models that use moving paddles to make waves.More robust validations, e.g., irregular wave-current interactions, wave-current interactions in non-parallel directions in the 3-D space, should be considered in the future work.The study of solitary wave-current interaction over a submerged obstacle is also in the initial research stage.This application is expected to provide a further contribution to the understanding the role of the tidal currents play in the interaction between tsunami waves and submerged obstacles.

Acknowledgements

This work was supported by the Fundamental Research Funds for the Central Universities (Grant No.2019B06514), the Scientific Research Program of Zhejiang Institute of Hydraulics and Estuary (Grant No.A17001).