一道动生电动势为电容器充电过程的严格解*

李俊鹏 琚 鑫 马朝华

(北京市海淀区教师进修学校 北京 100195)

1 引言

含电容器“单棒+导轨+电阻”模型是一类常见模型，在考查中多定性分析导体棒的运动情况，定性画出导体棒的v-t图像，计算导体棒的收尾速度等.往往学生能解得正确结果，但仍会提出很多疑问，如导体棒需要经过多长时间才能达到稳定速度？稳定速度为什么与电路中电阻R无关？电阻R在电路中起什么作用？导体棒变速滑动过程中有没有电磁能量的辐射等等.这些都在考验着教师对该部分知识的处理能力，本文就这些问题做些探讨，希望能回应以上疑惑.

2 分析

2.1 定性分析

如图1所示，水平面上有两根足够长的光滑平行金属导轨，两导轨间距为L，电阻可忽略不计.在导轨之间接有阻值为R的定值电阻和电容为C的不带电的电容器，导体棒质量为m,电阻忽略不计，并与导轨接触良好.整个装置处于方向竖直向下、磁感应强度为B的匀强磁场中.不考虑导体棒与轨道之间的摩擦和空气阻力.假设导轨长度足够长，磁场的范围也足够大.现给导体棒一个水平向右且足够大的初速度v0.

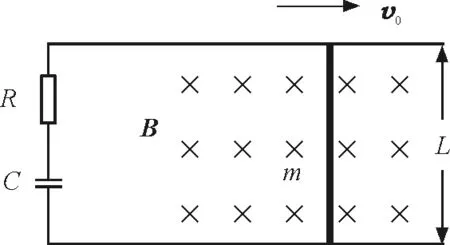
图1 实验装置示意图

我们先来对整个过程做一个定性的分析：由于导体杆向右运动，切割磁感线产生感应电动势，然后给电容器充电，随着电容器所带电荷量的增加，电容器极板间的电势差越来越大.直到电容器两端的电势差等于导体棒的动生电动势与电阻R两端的电势差之差，电路中不再有电流，充电结束.再看导体棒，由于导体棒所受安培力与导体棒的速度方向相反，因此导体棒将做减速运动，直到电容器充电完成，电路中电流为零，导体棒不再受安培力而保持匀速直线运动.

2.2 定量分析

从上述定性分析来看，物理情景清晰，但是却很难回答一些问题，比如要经过多长时间才能使电容器充电完成？这个过程中导体棒运动的位移是多大？于是，我们有必要对上述问题进行定量分析.

设某时刻t时，导体棒的速度为v，回路中电流为i，电容器某一极板上所带电荷量为q，则根据基尔霍夫方程有

(1)

再根据牛顿第二定律，有

(2)

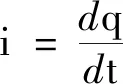
(3)

再将式(2)代入式(3)，整理后得

(5)

将式(5)对时间t求导，得到电流i随时间的演化关系

(6)

再将式(6)代入式(2)得

结合初始条件v(0)=v0，得

(7)

再对v从0到时刻t积分，得位移

(8)

上述表达式中方括号里的第1项是一个线性项，代表匀速直线运动，第2项是一个e指数的增加项，随着时间的推移，越来越趋近于定值CB2L2R.可见上述运动越来越趋近于一个匀速直线运动.

至此，我们完成了上述问题的全部数学推导，下面我们来就最终的稳态以及达到稳态所需时间和通过的位移进行讨论.

3 理想化处理

首先，稳态对应着充电结束，即电流i=0，由式(6)可知，此时应对应t=+∞.即电容器要用无限长的时间才能完成充电.分别将t=+∞代入式(7)和式(8)，发现式(8)是发散的，而式(7)可得收尾速度

v()

(9)

即导体棒会越来越趋近于这一速度.

我们再来计算达到稳定时，电容器极板所带电荷量Q为

(10)

此时电容器储存的电能E为

(11)

整个过程中电阻R上产生的电热Q热为

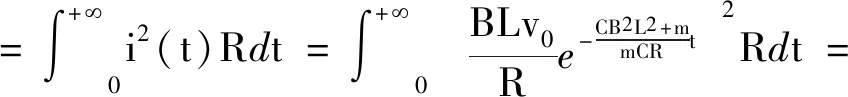
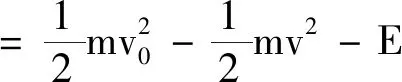
4 意义解释

下面，我们对电流i和速度v随时间变化的情况，做一些形象的定性描写.我们来绘制不同参数下i-t图像和v-t图像.根据式(6)和(7)可知，涉及的物理量有R,C,B,L,m和v0，由量纲可知，CB2L2具有质量的量纲，RC具有时间的量纲，因此RC也常被称作时间常数.

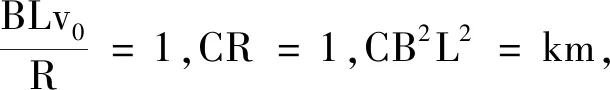
图2 i-t图 图3 v-t图

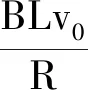
下面再就一个具体的情况进行计算：

取R=0.1 Ω，C=1 F,B=0.1 T,L=0.5 m,m=0.02 kg,v0=2 m/s，利用式(9)可知收尾速度为1.78 m/s，再计算当速度为1.80 m/s时所需时间的数值解为0.2 s，导体杆会在很短的时间内非常接近收尾速度.