利用刚体的平面平行运动证明平行轴定理*
2020-12-02申庆徽
申庆徽 陈 兵
(山东科技大学电子信息工程学院 山东 青岛 266590)
平行轴定理是刚体转动的一个重要知识点, 它反映了刚体绕相互平行的不同转轴转动时转动惯量之间的关系. 在大部分的教材中对该定理的证明都是从转动惯量的定义出发[1]. 本文从刚体的平面平行运动模型出发, 通过分析运动的动能推出了平行轴定理.如图1所示, 考虑任意刚体作平面平行运动, 纯滚动要求刚体与平面之接触点在接触那一瞬间为相对静止, 没有任何的相对滑动或滚动, 即相对速度为零, 此接触点即为速度瞬心. 此时, 刚体可以看成绕通过该瞬心的转轴转动, 且转动的角速度为ω. 设该刚体绕垂直于平面且通过瞬心转轴的转动惯量为IO, 则刚体运动的总动能为
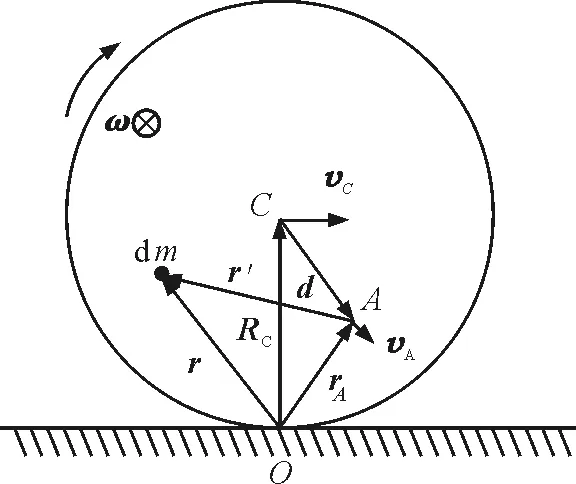
图1 刚体的纯滚动模型
(1)
另一方面, 由柯尼希定理可知刚体平面平行运动的总动能等于质心的动能与刚体绕质心的转动动能之和[2], 即
(2)
其中,IC为刚体绕过质心C轴的转动惯量,m为刚体的质量,vC为刚体质心C平动速度的大小. 由于平面平行运动刚体的角速度与相互平行的转轴位置无关[3],即质心平动的速度
vC=ω×RC
vC=|ω×RC|=ωRC
代入式(2)可得
(3)
对比式(1)和式(3)不难发现
(4)
此即平行轴定理.
上述分析并非只适用于转动瞬心的转动惯量与质心转动惯量之间的关系, 还可以推广到任意情况. 在图1中, 考虑任意转轴A, 设其相对瞬心的位置矢量为rA, 相对于质心的位置矢量为d. 设质元dm相对于O点的位置矢量为r, 根据前面的讨论知,质元dm的线速度为v=ω×r. 根据动能的定义
(5)
以A为参考点刚体的动能表达形式可以写为

(6)
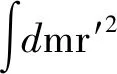
mω2(RC-rA)·rA
(7)
上式等号右边第一项可以理解为转轴A的平动动能,第二项表示刚体绕转轴A的转动动能,第三项表示对前两项动能的补偿量.不难看出,当rA=RC时即A点与质心C重合,式(7)即为柯尼希定理;当rA=0时,即A点与速度瞬心O重合,式(7)退化为式(1). 此外,比较式(7)与式(3)可得
(8)
整理得
IA=IC+m(|RC-rA|)2=IC+md2
(9)
此即刚体绕任意转轴A的转动惯量与质心转动惯量之间的关系,也就是平行轴定理.
