五面体可展桁架单元展开特性分析

2020-11-30彭笑雨林成新姚旗杨东升田昀

中国空间科学技术 2020年5期

彭笑雨，林成新，*，姚旗，杨东升，田昀

1. 大连海事大学船舶与海洋工程学院，大连 116026 2. 北京卫星制造厂有限公司，北京 100094

随着航天技术的发展，对空间结构的需求也朝着大型化、复杂化的方向发展。各种航天项目的机构规模越来越大，以满足不同需求的太空任务[1]。为了在复杂的空间环境中完成特定任务，人们设计了许多大型空间结构[2-4]。由于发射空间有限，因此航天器上广泛应用可展开机构[5]。由于其良好的应用前景，可展开机构已成为航空航天领域的研究热点之一[6-7]。20世纪80年代，兰利研究中心提出一种四面体单元的空间概念组装，随后Slysh等提出了一种在轨组装的方法[8]。随着机械臂和3D打印的发展，目前已经能利用3D打印技术制造微小桁架[9]，人们希望通过机械臂来实现在轨组装[10]，或者利用一种爬虫机器人和3D打印技术结合来实现桁架的组装。在工程应用方面，有美国AEC-Able公司开发的FAST和ADAM、TRW公司的太阳花展开天线[11]，以及浙江大学关富玲的扭簧驱动四面体天线[12]、燕山大学设计的构架式天线[13]、中国空间技术研究院的环形桁架式天线[14]、西安空间无线电技术研究院的大型网状天线[15]、上海交通大学陈务军的扭簧驱动空间展开桁架结构等[16]，而直接利用空间结构单元来进行组合较为少见。

因此，本文设计了一种五面体可展桁架单元并以此作为桁架基本结构，通过在轨装配的方式组装成空间桁架结构，用以搭建大型空间天线结构、太空站等复杂的结构等。

空间桁架广泛应用于支撑结构，目前主要基于桁架杆和桁架接头来进行组装。这种组装方式虽然灵活度高，但是对于固定的成型面来说，这种方式使得组装复杂。以五面体可展桁架单元作为桁架可展结构的基本单元，具有多方面的优点。相对于桁架杆和桁架接头的组装方式而言，以五面体可展桁架单元多为基础，能减少组装的复杂程度。并且该单元在存储运输时，处于收拢状态，能够节省存储空间，并且方便大批量运输；到达目标位置后，通过一定条件使其展开成设计的形状并保持稳定。使用时，以展开后的五面体可展桁架单元为基础，可以进行大型空间桁架的拼接与组装。

1 结构及自由度分析

1.1结构分析

所设计的五面体可展桁架单元展开过程中的结构如图1(a)所示，其完全展开后如图1(b)所示。该五面体可展桁架单元的连接均为铰链连接。

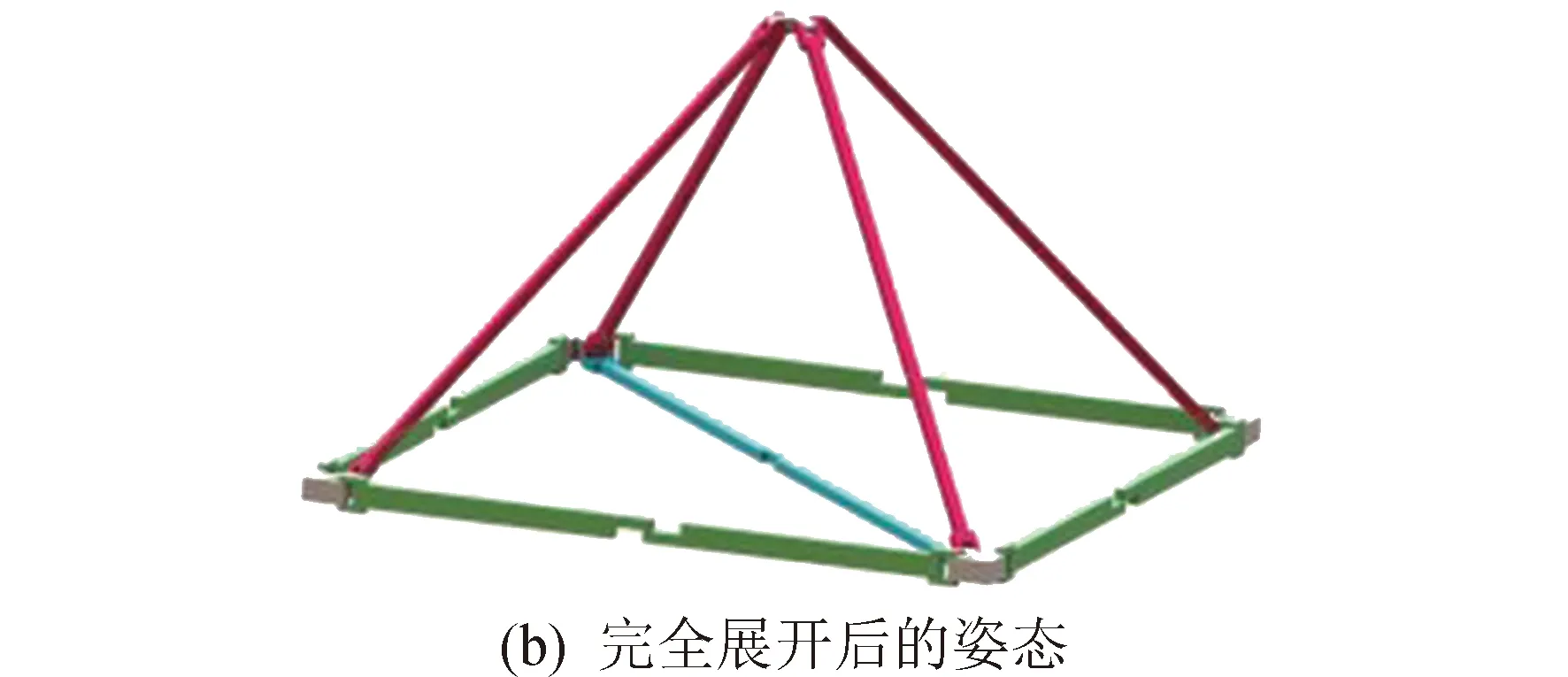
图1 五面体可展桁架单元的展开形态Fig.1 The expanded form of pentahedral deployable truss unit

五面体可展桁架单元完全展开后，该桁架单元必须能保持稳定，这样，以该五面体可展桁架单元组成的大型桁架才能保持稳定。参考Maxwell几何体系稳定性必要判据[17]，对该五面体可展桁架单元进行分析：

e≥αν-β

(1)

式中：e为边数；v为顶点数；α为维数；β为自由度数。对于空间机构，α=3，β=6。

五面体可展桁架单元展开后，e为9，v为5，等式左右均为9，满足公式(1)条件，公式成立。因此，以该五面体可展桁架单元结构作为基本桁架单元能保证基本单元结构的稳定，是实现整体结构稳定的前提。

以五面体可展桁架单元作为基本单元，可以组合成多种类型的桁架结构，如图2所示。

图2 五面体可展桁架单元组成空间结构Fig.2 Spatial structures composed by pentahedral deployable truss units

在基本单元进行连接时，如图3所示，通过在该基本单元上设置预留的连接杆，利用接头将两个五面体可展桁架单元进行连接。连接的接头可以使用卡扣式的快速接头，或者利用记忆合金接头。在连接时，只需将五面体可展桁架单元上预留的连接杆插入连接的接头，即可实现连接。对于不同的成型面，可通过改变接头与两个五面体可展桁架单元之间角度来实现。

图3 连接杆Fig.3 Connecting rod

1.2 自由度分析

如图4所示，以五面体可展桁架单元的锥点o为原点建立空间直角坐标系。图4中所有连接均为铰链连接，点1～23处的转动轴在坐标系中的矢量分别为S1～S23，其中转动轴方向矢量S1、S2、S17、S16垂直于平面xoz，转动轴方向矢量S7、S6、S12、S11、S21、S22、S23垂直于平面yoz，S3、S4、S5、S20、S19、S18、S15、S14、S13、S10、S9、S8垂直于平面xoy。

图4 五面体可展桁架单元的坐标系Fig.4 The coordinate system of pentahedral deployable truss unit

则各处转动副的旋量分别为：

(2)

式中：x1～x5、x8～x10、x13～x20为点1～5、8～10、13～20的x方向坐标，y3～y15、y18～y23为点3～15、18～23的y方向坐标，z2、z6、z11、z16、z21～z23为点2、6、11、16、21～23的z方向坐标，且z2=z6=z11=z16，z21=z23。

对五面体可展桁架单元参考机构的独立闭环公式为：

L=p-n+1=5

(3)

式中：L为独立闭环数；p为机构的铰链数；n为机构的构件数。

由于该五面体结构拥有5个独立闭环，因此，整个五面体可展桁架单元的闭环旋量约束方程为：

(4)

式中：ωi，i=1,2,…，23，为铰链的旋量坐标；0为6维列向量。

将式(4)写成矩阵形式:

MN=0

(5)

将式(2)中各转动副旋量值带入矩阵M，则矩阵M的秩为：

R(M)=22

(6)

由式(6)可知，矩阵M的秩为22，而矩阵M的列数为23，矩阵零空间的维数为列数减去矩阵的秩，因此可以得到该五面体可展桁架单元的自由度数为1。

2 可展五面体桁架单元的运动学分析

2.1位置分析

以五面体桁架单元的锥点o点为顶点在结构中建立空间直角坐标系如图5所示。以D点、

I点为例对五面体可展桁架单元进行运动学分析。五面体桁架单元展开时，在D点施加驱动，CD、DE杆绕着D点进行转动。其中，D点的运动可以视为绕着E点的旋转。I点的运动可视为绕着H点的旋转。

图5 五面体可展桁架单元Fig.5 Pentahedral developable truss unit

为了表达各杆件之间的相对位置和姿态，通常采用D-H方法[18]，其坐标变换所需要的参数分别是绕x轴转动的角度，沿x轴移动的距离，绕z轴转动的角度，沿z轴移动的距离。则o点到E点的坐标变换矩阵TE为：

将坐标轴从o点变换到E点后，杆DE在以E点为原点的变换后的坐标系中的位置如图6所示。

通过坐标变换得到D点相对于E点的变换矩阵TD为：

式中：l2为杆CD、DE的长度;∠EDC为2θ1。

图6 以E点为原点的坐标系中的杆DE的位置Fig.6 Location of rod DE in coordinate system with point E as origin

则在以o为原点的坐标系中D(xD,yD,zD)点的坐标为：

(7)

式中：MD为D点在以o点为原点的坐标系下的坐标矩阵。

由式(7)可得出D点的幅值位置方程sD为：

(8)

根据机构各构件所构成的封闭矢量多边形OABLCDEKFG，可得出:

(9)

将式(9)分别向x、y、z三个轴投影，最终可以得到D点位置约束方程：

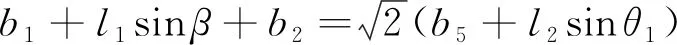
(10)

又因为在D点的驱动已知，结合D点位置方程(7)、D点幅值位置方程(8)和D点位置约束方程(10)，可以描绘出D点的位置幅值变化关系。

同理，I(xI,yI,zI)点的坐标矩阵MI为：

(11)

式中：l3为杆HI、IJ的长度;b4为H点到F点的距离;∠HIJ为2θ2。

根据式(11)可得出I点的幅值位置方程sI为：

(12)

根据机构各构件所构成的封闭矢量多边形OGFHIJNP，可得出：

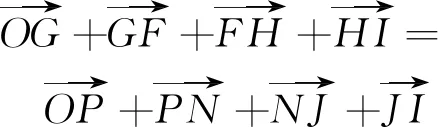
(13)

将式(13)分别向x、y、z三个轴投影，最终可以得到I点的位置约束方程为：

b1+l1sinβ=l3sinθ2

(14)

在驱动已知的条件下，结合方程I点的位置方程(11)、I点的幅值方程(12)和I点的位置约束方程(14)，可以得出I点的位置幅值变化关系。

2.2 速度分析

对D点进行速度分析，将D点位置方程(7)中的坐标对时间求导，可以得到D点的速度方程为：

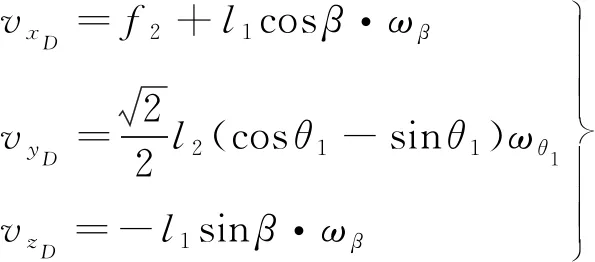
(15)

其中：

将D点的位置约束方程(10)对时间求导，可得D点的速度约束方程为：

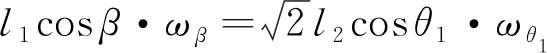
(16)

根据式(15)可得D点的速度幅值方程vD为：

(17)

结合D点的速度方程(15)、D点的速度约束方程(16)、D点的速度幅值方程(17)，可求出D点的速度幅值变化关系。

同理，将式(11)中的坐标对时间求导，可得I点的速度方程为：

(18)

将式(14)对时间求导，得到I点的速度约束方程为：

l1cosβ·ωβ=l3cosθ2·ωθ2

(19)

根据式(18)可得到I点的速度幅值方程vI为：

(20)

结合I点的速度方程(18)、I点的速度约束方程(19)、I点的速度幅值方程(20)，可求出I点的速度幅值变化关系。

2.3 加速度分析

将D点的速度方程(15)对时间求导，可得D点的加速度方程为：

(21)

其中：

将D点的速度约束方程(16)对时间求导，可得D点的加速度约束方程为：

(22)

根据式(21)可得到D点的加速度幅值方程aD为：

(23)

结合D点加速度方程(21)、D点加速度约束方程(22)和D点加速度幅值方程(23)，可求出D点的加速度幅值变化关系。

同理，将式(18)对时间求导，可得I点的加速度方程为：

(24)

其中：

将式(19)对时间求导可得I点的加速度约束方程为：

(25)

根据式(24),可得I点的加速度幅值方程aI为：

(26)

结合I点的加速度方程(24)、I点的加速度约束方程(25)和I点的加速度幅值方程(26)，可求出I点的加速度幅值变化关系。

3 扭簧驱动可展五面体桁架单元动力学分析

3.1系统动能的求解

根据之前对五面体可展桁架单元做的自由度和运动学分析可知，五面体可展单元的运动位置、速度、加速度以及角度β、θ2都与角度θ1有关，因此取广义坐标为θ1。只要确定了θ1、ωθ1、αθ1，就能确定机构整体的运动情况。五面体可展桁架单元系统的总动能为14根连杆Ti与4个连接块的动能Tj之和。关于连接块的动能求解，可直接将连接块的质量等效于连接节点上。而连杆的运动为空间运动，求解会相对复杂。如图7所示在五面体可展桁架单元中以o为原点建立全局坐标系，在R、V、D、Q处添加扭簧约束，以ED杆为例求解连杆的动能。在E点建立局部坐标系E-xEyEzE如图7所示。

图7 整体坐标系中建立局部坐标系Fig.7 Establishing local coordinate system in the whole coordinate system

则连杆ED上任意位置的一点S在全局坐标系o-xyz可以用公式表示为：

rs=RE+AEuS

(27)

式中：rs为S点在全局坐标系中的坐标;RE为E点在全局坐标系中的坐标矩阵;AE为E点的局部坐标系相对于全局坐标系的旋转矩阵;us为S点在局部坐标系E-xEyEzE的空间坐标。

us在局部坐标系E-xEyEzE的空间坐标可以通过uE和uD来表示：

(28)

式中：uE、uD为E点、D点在局部坐标系E-xEyEzE的空间坐标;c为S点到E点的距离;l2为杆ED的长度。

将式(27)对时间求一阶导，并将式(28)带入可得到S点速度方程为：

(29)

式中：JS为雅克比矩阵。

由于在五面体可展桁架单元中所采用的局部坐标系相对于全局坐标系的旋转矩阵均与广义坐标无关，因此可得：

(30)

将式(29)对时间求导，并将式(30)带入，可得到S点加速度方程为：

(31)

则连杆ED的动能TED表达式为：

(32)

式中：ρ为连杆ED的线密度;m2为连杆ED的质量。

运动学分析时已经给出了角度β与θ1之间的关系，旋转矩阵和各个点在全局坐标系中的坐标都可用前面运动学的分析方法求出，因此由以上条件可以求出连杆ED的动能。同理，可以求出其他连杆的动能。

连接块L与连杆AB连接，因此可直接将连接块L的质量等效于连接节点B点上。所以，连接块L以A点为原点建立局部坐标，连接块L的动能为：

(33)

式中：m4为连接块L的质量；AA为A点的旋转矩阵；RA为A点的全局坐标；uB为B点在以A为原点的局部坐标系下的空间坐标。

结合以上条件，可以求出连接块L的动能。同理，其他连接块的动能可依次求出。结合式(32)(33)，求出所有连杆动能和连接块动能后，五面体可展桁架单元系统的总动能T为：

(34)

式中：

这里，杆长为l1的杆质量为m1、杆长为l2的杆质量为m2，杆长为l3的杆质量为m3，连接块质量为m4，β、θ2与θ1之间的关系可通过式(10)(14)得出。

3.2 系统势能的求解

D点的扭簧的布置示意如图8所示，其中∠EDC为2θ1。

图8 驱动扭簧布置示意Fig.8 Layout of driving torsion spring

由于五面体可展桁架单元主要考虑无重力环境的应用，因此该单元的系统势能只来自扭簧提供的弹性势能。整个五面体可展桁架单元中，扭簧被布置在D、Q、R、V四个点处。扭簧的初始扭矩为M，刚度系数为k。则扭簧在展开过程中的弹性势能为：

(35)

3.3 动力学方程建立

采用拉格朗日函数，取广义坐标为θ1，结合式(34)(35)，对于单个五面体可展桁架单元而言，摩擦力产生的影响很小，可以忽略，所以系统受到的广义力为0。因此建立动力学微分方程为：

(36)

将式(34)(35)带入方程(36)，化简可得扭簧驱动五面体可展桁架单元的动力学方程为：

(37)

4 仿真验证

4.1运动学仿真验证

将五面体可展机构模型导入Adams仿真软件中。在该模型中，设定OA、OG的长度b1为20 mm，AB、GF的长度l1为515.1 mm，CD、DE长度l2为270 mm，F点到K点的x方向距离b2为40 mm，z方向距离b3为5 mm，H点到F点的距离b4为10 mm，K点到E点的距离b5为30 mm，HI、IJ的长度l3为384.3 mm。在D点处施加一个匀速转动的驱动M，其角速度为30(°)/s。初始时，五面体可展机构的角度∠EDC=30°。设置仿真时间为5 s，步长为500。仿真后，分别从Adams中导出D点、I点的位置、速度和加速度的幅值曲线，将得出的仿真结果与理论推导计算的结果进行对比，其对比结果如图9所示。

图9 理论计算与Adams仿真对比曲线Fig.9 Comparison between theoretical calculation and Adams simulation

从Adams的仿真结果可以看出，D点和I点在位移曲线和速度曲线中，理论分析结果与仿真结果几乎完全吻合，而在加速度仿真中，由于仿真软件分析时将模型视为纯刚性物体，现实中纯刚性的物体是不存在的，因此模拟中出现震动和冲击，导致个别值与理论计算的结果差异较大。但总体上，理论推导的运动学方程与仿真结果基本拟合。因此，该理论分析可以很好地描述空间五面体单元的运动学展开过程。

4.2 不同扭簧刚度下动力学仿真分析

图10 不同刚度下D点加速度曲线Fig.10 Acceleration curve of point D under different stiffness

由图10可知，扭簧刚度系数的增大，对五面体可展桁架单元展开的运动参数的变化趋势没有明显影响。当扭簧刚度从1增加到2时，时间减少了约0.27 s，展开造成的冲击增大1倍。结合图10和式(30)可以看出，节点的加速度不仅与扭簧的驱动力有关，还和节点位置和速度有关。在展开后期，节点位置和节点速度对节点加速度的影响比较明显。