基于低轨稀疏星座的蓝绿激光对潜定位研究

徐伟证，康国华,*，刘佳露，张雷，刘宗强

1. 南京航空航天大学 航天学院，南京 210016 2. 西安卫星测控中心，西安 710043

潜艇具有隐蔽性强、高效打击和长时续航的优势，是国家现代化军事力量的重要组成部分。由于潜艇特殊的工作环境，其在信息传输和导航定位方面都存在较多问题[1]。特别是潜艇定位，由于电磁波信号穿透海水的能力极差，潜艇在水下不能使用全球卫星导航系统(global navigation satellite system,GNSS)进行定位，因此一直未有高精度定位方案，亟需有效的解决方案[2]。蓝绿激光方向性好,工作频率高,通信频带宽,数据传输能力强，且衰减系数低，其水下平均衰减率只有甚低频的1/15，超低频的2/3，可以与深达几百米下的潜艇进行通信[3-4]。水下蓝绿激光通信应用潜力巨大，世界各国都极为重视，目前机载、临近空间和星载蓝绿激光对潜艇通信均已经得到实际验证，取得良好的效果。其中基于低轨卫星的蓝绿激光星潜双向通信完全可行，也是现阶段实现蓝绿激光对潜通信的最优方案[5-8]。

信号光可以作为数据传输的载体，传输的数据是经过编码的数据流，可在接收端通过译码恢复原始数据[9]。激光双向通信单程测距方案，采用伪随机码作为测距码，通过对发射时的本地时钟信号和接收后恢复的时钟信号进行相位比对，实现激光测距[9-15]，因此激光通信的同时进行测距具有了基础。在卫星导航定位方面，利用中国北斗3颗地球同步轨道卫星与高度表可实现三星无源定位，验证了“多星伪距+高度表”定位的可行性[10-11]。近年来也有学者研究地面终端通过多次接收单颗卫星实现定位的方式，仿真表明单颗低轨卫星连续观测下定位精度约500 m[12-13]。

本文将上述研究结合起来，在激光通信测距一体化以及三星无源定位和单星多普勒定位的技术基础上，针对潜艇水下定位需求，提出采用蓝绿激光的低轨稀疏星座定位方案。

1 低轨稀疏星座定位原理

1.1 低轨稀疏星座定位方案

低轨卫星对潜艇通信测距如图1所示，潜艇根据低轨星座的星历预测卫星过顶的时间窗口，并预先在相应区域准备建立激光通信测距链路。低轨卫星以蓝绿激光光束作为载波，应用码元相位同步测距体制，将导航电文数据及测距标识编码进行调制和播发。潜艇接收激光信号后，通过解调获取低轨卫星激光终端的测距标识时刻，并对潜艇自身发射编码器的相位进行采样，从而提取测距值，获得卫星和潜艇间的距离。假定星座过境期间潜艇保持水下静止，经过一定时间间隔完成至少2次通信测距，联合2组观测数据与潜艇自身高程测量信息进行定位解算，实现基于星潜定位算法实现潜艇的水下定位[6-8,14-15]。

1.2 激光通信测距

激光通信测距一体化技术以激光光束为载体，将测距和通信信息共用同一束激光和硬件平台，同步完成通信和测距双重功能[9,15]。传统激光测距是通过激光发射器将序列码进行相位调制后发往被测目标，捕获目标反射回来的激光信号并解调恢复出序列，比对相位序列以确定相位时延差，进而确定激光往返时间间隔来实现测距[15]。考虑到低轨稀疏星座的过境窗口、潜艇的隐蔽性和水下工作环境需求，本文采用双向单程测距体制来实现潜艇伪距测量。其中双向单程测距体制如图 2所示[15]。

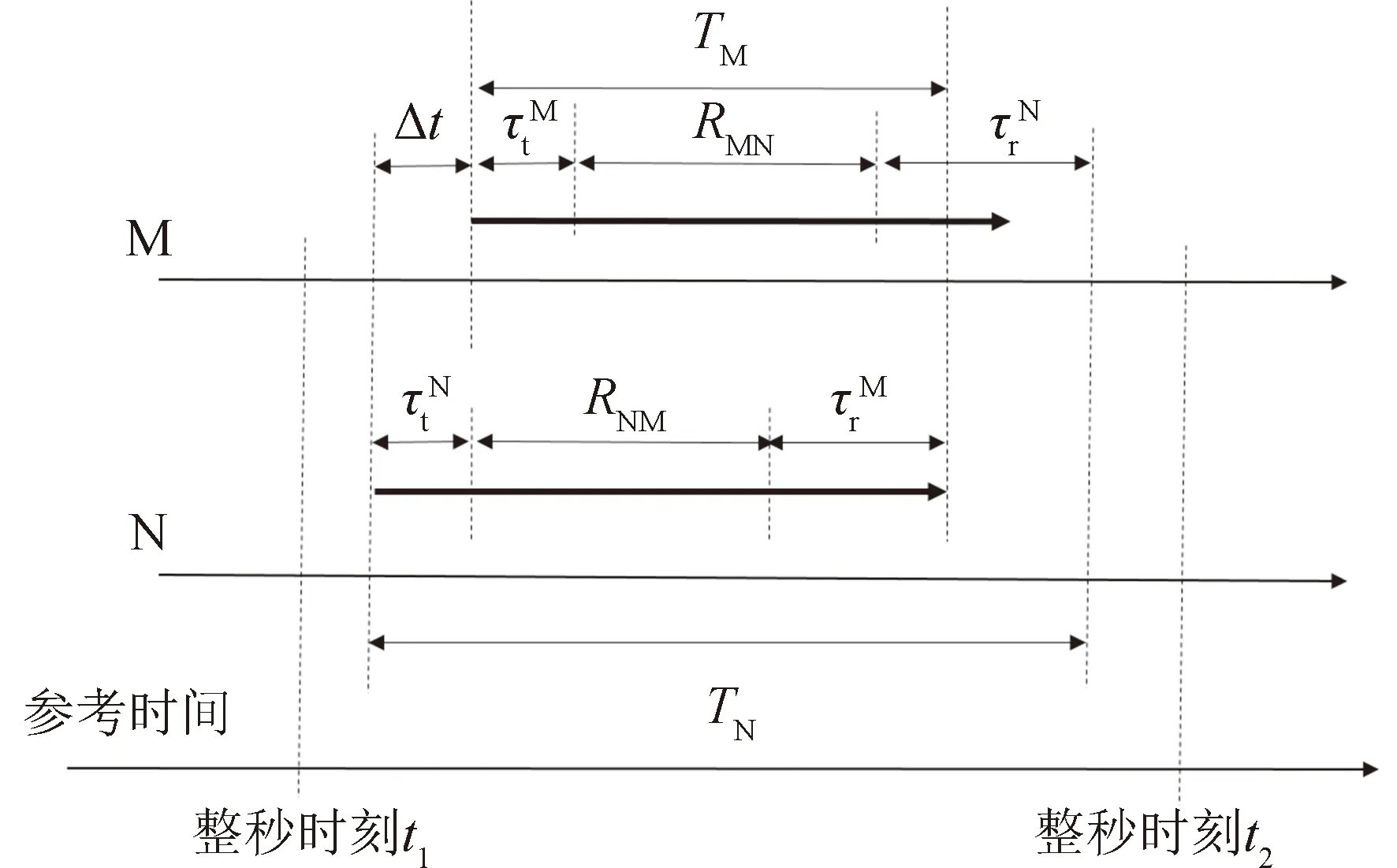
图2 双向单程测距原理Fig.2 Schematic diagram of dual one-way ranging

M，N表征了潜艇和卫星两个测距对象，RNM，RMN为测距对象即卫星和潜艇的距离，卫星与潜艇间存在时差Δt，激光通信均存在发送时延τt、接收时延τr，若时差满足[15]：

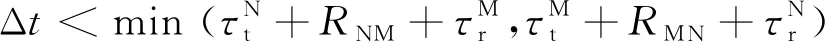
(1)

实际计时信息可以表示为[15]：

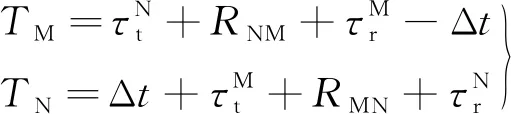
(2)

卫星和潜艇间距离为：

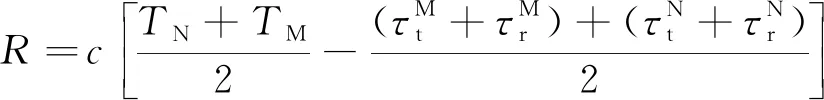
(3)

式中：c为光速。

在单程测距体制基础上，采用码元相位同步测距，其工作机制如图3所示，低轨卫星激光发射器基于星钟倍频产生工作时钟，在同步脉冲时刻，由测距编码模块产生基带数据，调制后作为测距标识，数据帧插入“计时”信息。潜艇接收激光信号并进行采样、码同步、帧同步等处理，解调出测距标识，并在数字控制振荡器(numerically controlled oscillator，NCO)时标模块比对，完成高精度“计时”，进而结合本地“计时”信息计算测距值[15]。

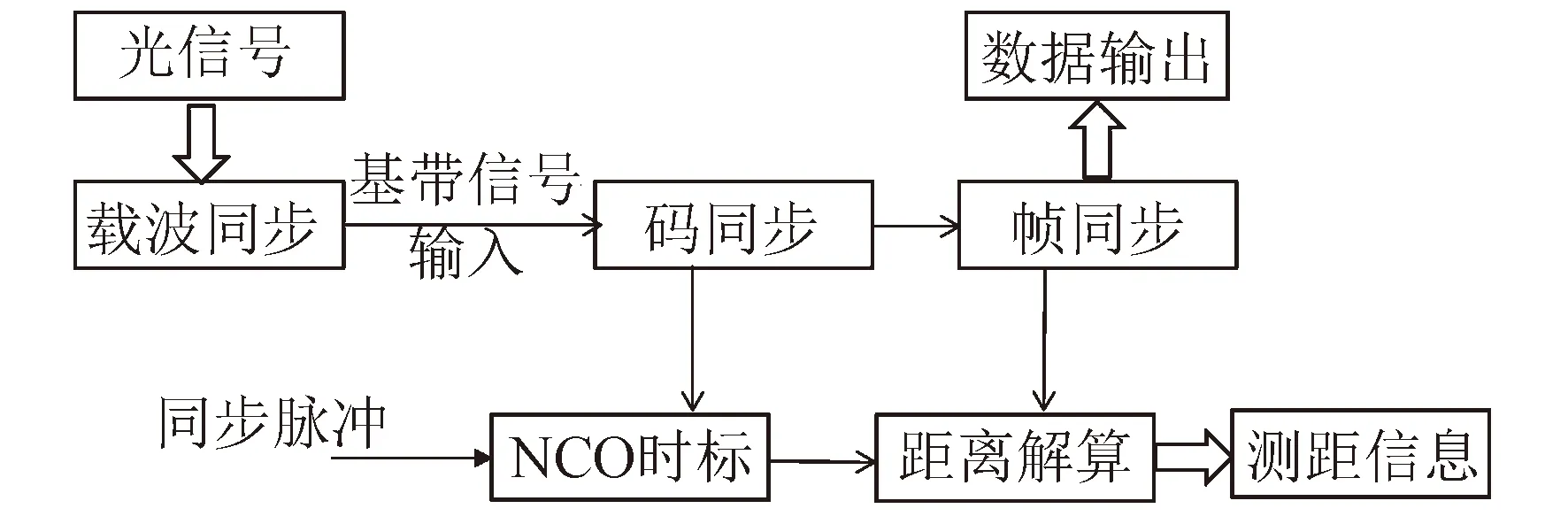
图3 数据位同步测距原理Fig.3 Responsive ranging working mechanism

1.3 低轨星座定位算法

北斗三星无源定位是依靠3颗地球同步轨道卫星的伪距测量值和高程测量值构建4个观测方程，求解用户位置和伪距钟差[14,17]。考虑到低轨卫星轨道高度低，3颗卫星位置关系相近，几何构型较差，在进行定位解算时观测值相关性较强，无法实现最小二乘定位解算。单星多普勒定位通过累积一定时间多个历元的量测数据进行定位，反映了定位目标和卫星间距离变化率。

综合考虑三星无源定位和单星多普勒定位原理，不失合理性，假定潜艇位置静止在水下某一点，低轨星座过境期间多次采集观测数据，且认为该时间段内卫星时钟稳定，从而获取多组观测值来参与几何位置解算。星座过境通信测距原理如图 4所示，t1时潜艇与低轨星座进行通信测距获得3个伪距测量值ρt1,i(i=1,2,3)，经过时间间隔Δt，到t2时刻再次接收数据获取伪距测量值ρt2,i(i=1,2,3)。依靠低轨星座的星历数据即可获得测量时刻的卫星精确位置坐标(xi,yi,zi)(i=1,2,3)，并通过潜艇的高程测量计可获得高程测量值H，与t1、t2时刻两组伪距测量值构成7个观测方程，解算潜艇位置(xu,yu,zu)和钟差，通过最小二乘和牛顿迭代法反复运算，从而实现潜艇的快速实时导航定位。

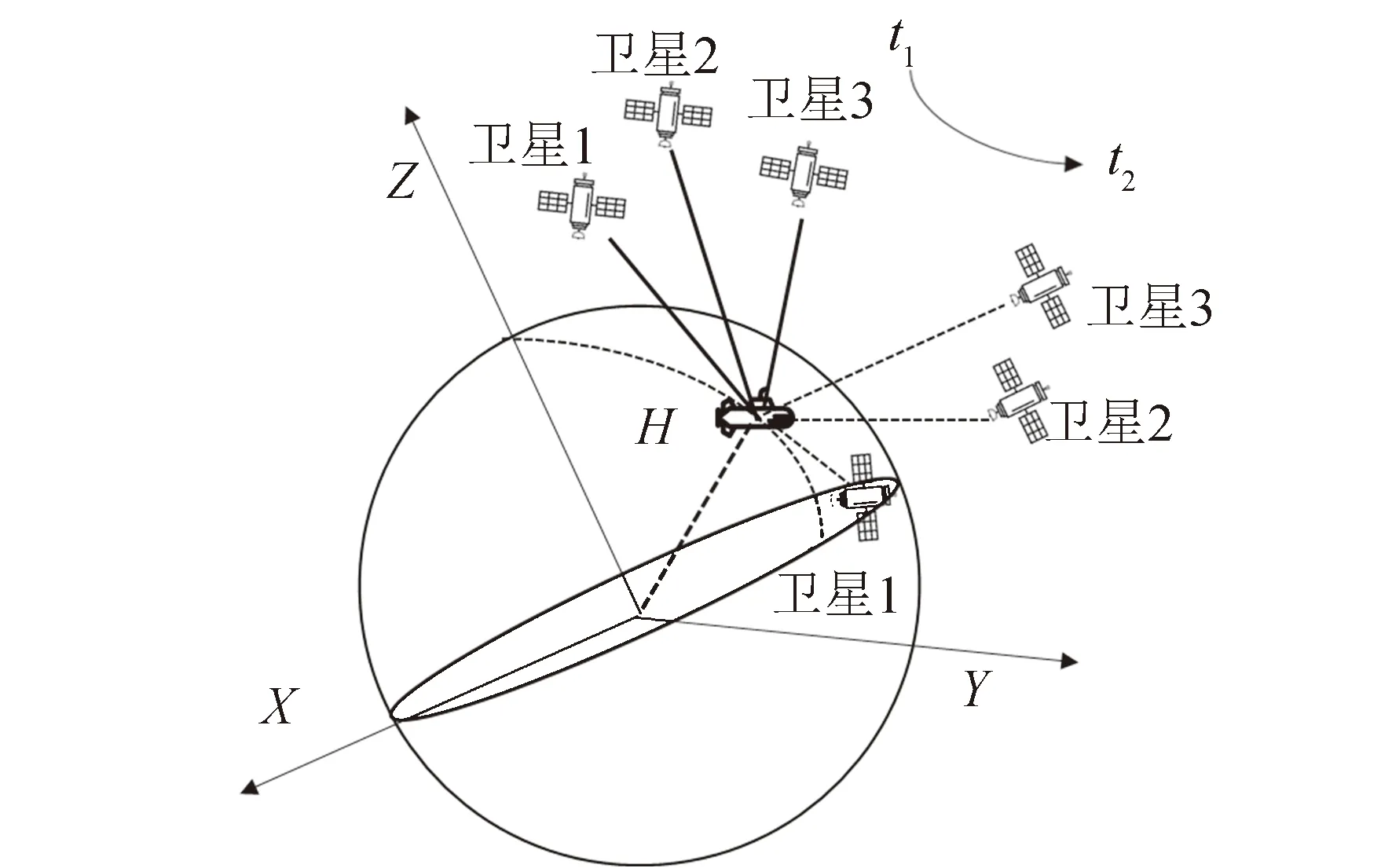
图4 低轨星座与潜艇通信测距原理Fig.4 LEO constellation and submarine communication ranging principle diagram

潜艇与低轨星座通信过程中，假定潜艇位置在2次通信间隔内保持不变，随着星座过境过程，其测得的量测值可表示为[19]：

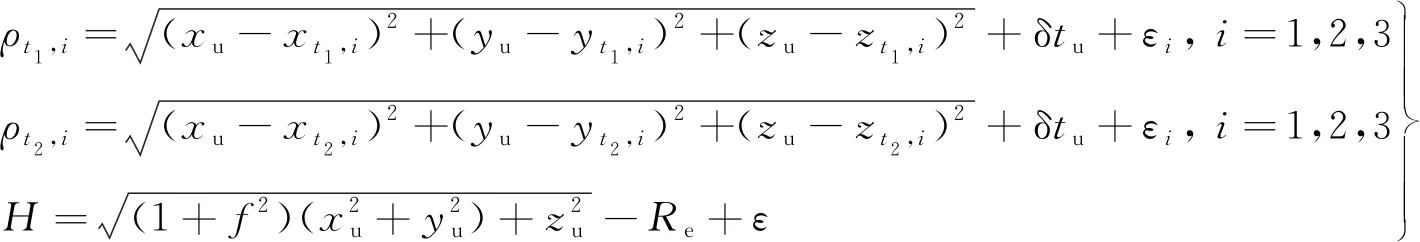
(4)

式中: (xt,i,yt,i,zt,i)(t=t1,t2,i=1,2,3)为3颗卫星在t1,t2时刻ECEF坐标系下位置坐标;δtu为潜艇与卫星间等效钟差距离;Re为地球半径;f为地球偏心率;εi为伪距测量过程中激光在空气、水下传播、测量间隔期间的组合误差；ε为高程测量误差。通过7个观测方程对4个待估计量,包括xu、yu、zu、δtu,进行迭代求解。在牛顿迭代解算过程中，需要将方程组(4)中的非线性方程在[Xk-1,δtu,k-1]T处进行线性化，其中对方程中待估参数的偏导数矩阵G和偏差输出量矩阵b如下所示：

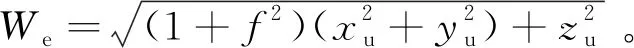
根据当前观测值数据计算出G和b后，可利用最小二乘法求解位置改正量ΔXu和激光接收机钟差改正量δtu：

[ΔXu,Δδtu]=(GTG)-1GTb

(5)

并利用位置改正量和接收机钟差改正量修正位置和接收机钟差估计值：

(6)

如果修正量满足一定精度要求或迭代次数达到迭代上限，则获得潜艇坐标Xu=[xu,yu,zu]和激光接收机钟差δtu。

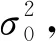
高斯分布时定位误差标准差σpos与空间位置精度因子PDOP、用户等效距离误差标准差σUERE的关系为：

σpos=PDOP×σUERE

(7)

PDOP反映星潜几何关系对定位误差的影响，在相对测量误差下，星座的几何分布对用户定位误差的放大量。

2 低轨稀疏星座分析与优化

2.1 低轨稀疏星座覆盖性分析

低轨稀疏星座的几何构型直接关系到星座覆盖范围，以低倾角星座为例，其主要服务区域的覆盖情况如图 5所示。星座过境期间潜艇在服务区域可同时与1～3颗卫星进行通信和测距，实现信息传输和导航定位解算。低轨卫星运动速度快，星座过境时间短，需要潜艇根据星座星历预测卫星过境时间窗口，或采用主动取报方式建立通信联系，在短时间内完成多次通信测距服务[18-19]。低轨稀疏星座可以实现对服务区域的短时间重访，通过分不同组合优化设计低轨星座几何构型，可以实现对潜艇信息传输和导航定位的最优服务。

图5 低轨星座对服务区域的覆盖情况Fig.5 LEO constellation coverage of service areas

图6 低轨星座覆盖性分析Fig.6 LEO constellation coverage analysis

低轨星座对于潜艇的覆盖情况如图 6所示，设地心O，3颗低轨卫星覆盖面可视球冠分别为AB,CD,EF，3颗卫星的共同覆盖区域为M，该区域内可同时接收3颗卫星通信信号，获取伪距观测量，为潜艇定位的最佳区域。假设卫星激光发射器最大半张角α，可实现对星下一定区域的覆盖。单星的覆盖范围取决于激光发射器最大半张角α，对应卫星覆盖的圆心角Ψ。该圆心角ψ受轨道高度Hs和最小地面仰角εmin约束，计算如下[20]：

(8)

本文考虑地面最小通信仰角εmin为10°[7-8]，则可根据卫星轨道高度确定单颗卫星的覆盖范围，进而设计低轨稀疏星座构型，完成对主要服务对象的最佳覆盖。

2.2 低轨稀疏星座参数优化

本文主要以一带一路海域为服务对象，特别是中国东海、南海区域，对低轨稀疏星座的轨道高度、轨道倾角、覆盖范围和重访时间等提出了约束条件。

以地面主要服务区域的纬度范围为约束，设计低轨卫星轨道倾角在15°～25°间。激光通信测距会在海面产生光斑，从潜艇隐蔽性考虑，卫星轨道高度不宜太低，以免暴露潜艇的工作区间。结合星座的寿命及空间环境影响，轨道高度宜选择在800～1 000 km。低轨卫星导航定位对星座的几何构型要求较高，容易出现伪距观测量相关性较强而无法进行最小二乘解算的情况。本文通过约束3颗卫星的升交点赤经(right ascension of ascending node,RAAN)和真近点角，使得低轨稀疏星座近似为等边三角形，以期获得较优的星座构型。

针对主要服务区域的覆盖性和定位需求，为探讨星座构型对定位性能影响的规律，本文组合设计低轨稀疏星座的轨道高度、轨道倾角与升交点赤经和真近点角，共组成27种不同星座进行仿真分析。星座参数方案如表 1所示。

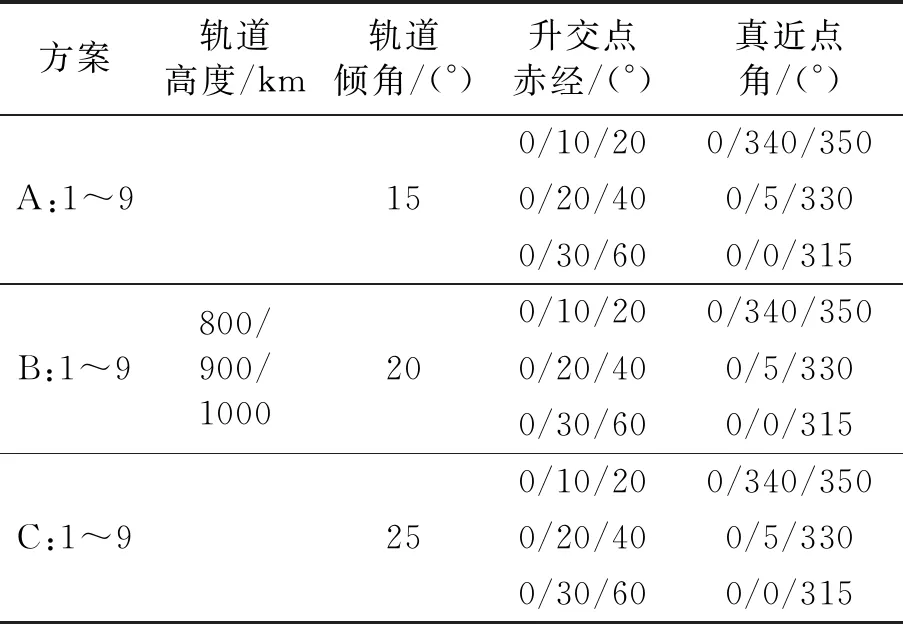
表1 低轨稀疏星座参数设计方案

2.3 低轨稀疏星座定位性能

本文将27种低轨稀疏星座组合依照控制变量法，依次按照不同轨道高度、轨道倾角、升交点赤经分成9组，每组3种星座，来分析星座参数对定位结果的影响。设计定位目标点[15°(N)，115°(E)，-100 m]在中国南海区域，数据选取伪距观测值采样间隔1 min，误差超过500 m视为无效定位，置零处理。时钟误差作为待估参数，潜艇等效测距误差包括低轨卫星定轨精度，激光在空气、水下传播误差等，设为方差为36 m2，均值为零的高斯分布[17-18]。从仿真场景中获取卫星精密星历、覆盖情况、目标点定位真值等数据，验证低轨稀疏星座对潜艇的定位算法，分析低轨星座轨道高度、轨道倾角、升交点赤经对定位结果的影响。对比结果如图7～图9所示，分析可知：

1)由图 7可见，在轨道高度800～1 000 km区间，多数低轨稀疏星座组合中不同轨道高度对潜艇定位误差影响不大，仅在轨道倾角15°，升交点赤经差值序列为10°时有一定差异，说明轨道倾角、升交点赤经和真近点角确定后，轨道高度小范围变化对定位结果影响不大。

2)由图 8可见，轨道倾角15°的星座组合最终定位误差明显偏大，轨道倾角20°和轨道倾角25°定位误差相近，但轨道倾角25°时存在仿真采样间隔(1 min)内无法实现有效定位的情况，需要延长采样间隔才能满足定位需求。

3)由图 9可见，在轨道高度、轨道倾角、真近点角均保持一致，仅对比不同升交点赤经等差序列，9组星座组合对比均显示升交点赤经等差序列为20°时，定位结果误差相对较小。

通过对27种组合星座的仿真设计和定位误差分组对比分析，确定轨道高度800～1 000 km，轨道倾角15～25°范围内，星座参数变化对定位误差影响趋势较明显，但不同星座最终定位误差差值范围较小，绝大部分差值在10 m内，少数在30～40 m间。其中轨道高度900 km，轨道倾角20°，升交点赤经分别为0°，20°和40°，真近点角分别为0°，5°和330°的稀疏星座，对潜艇定位性能较好。

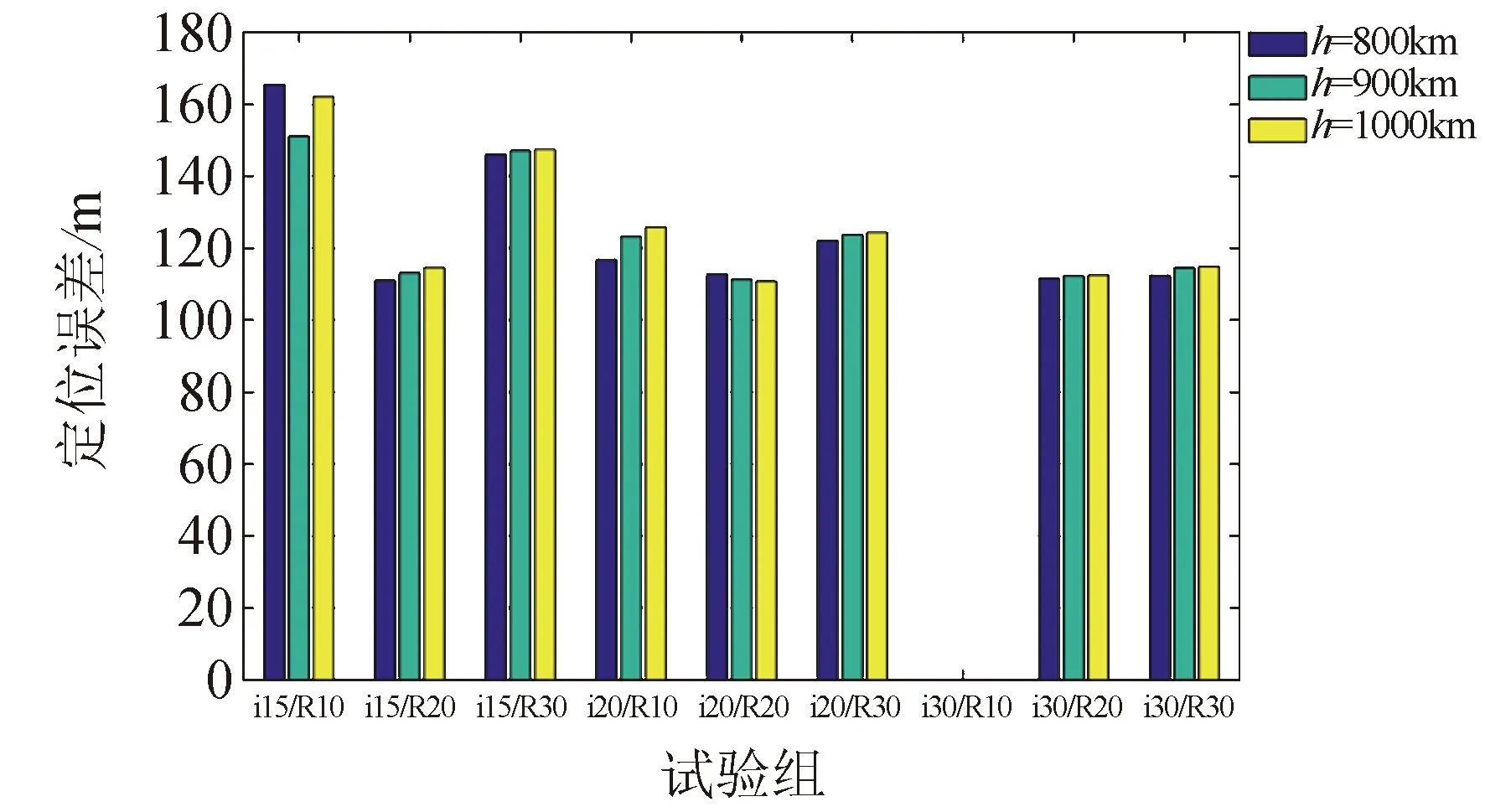
图7 轨道高度对定位误差的影响 (i15/R10：轨道倾角15°，升交点赤经等差序列10°)Fig.7 Influence of orbital height on positioning error (i15/R10: the orbital inclination is 15°, the equal difference of RAAN is 10°)

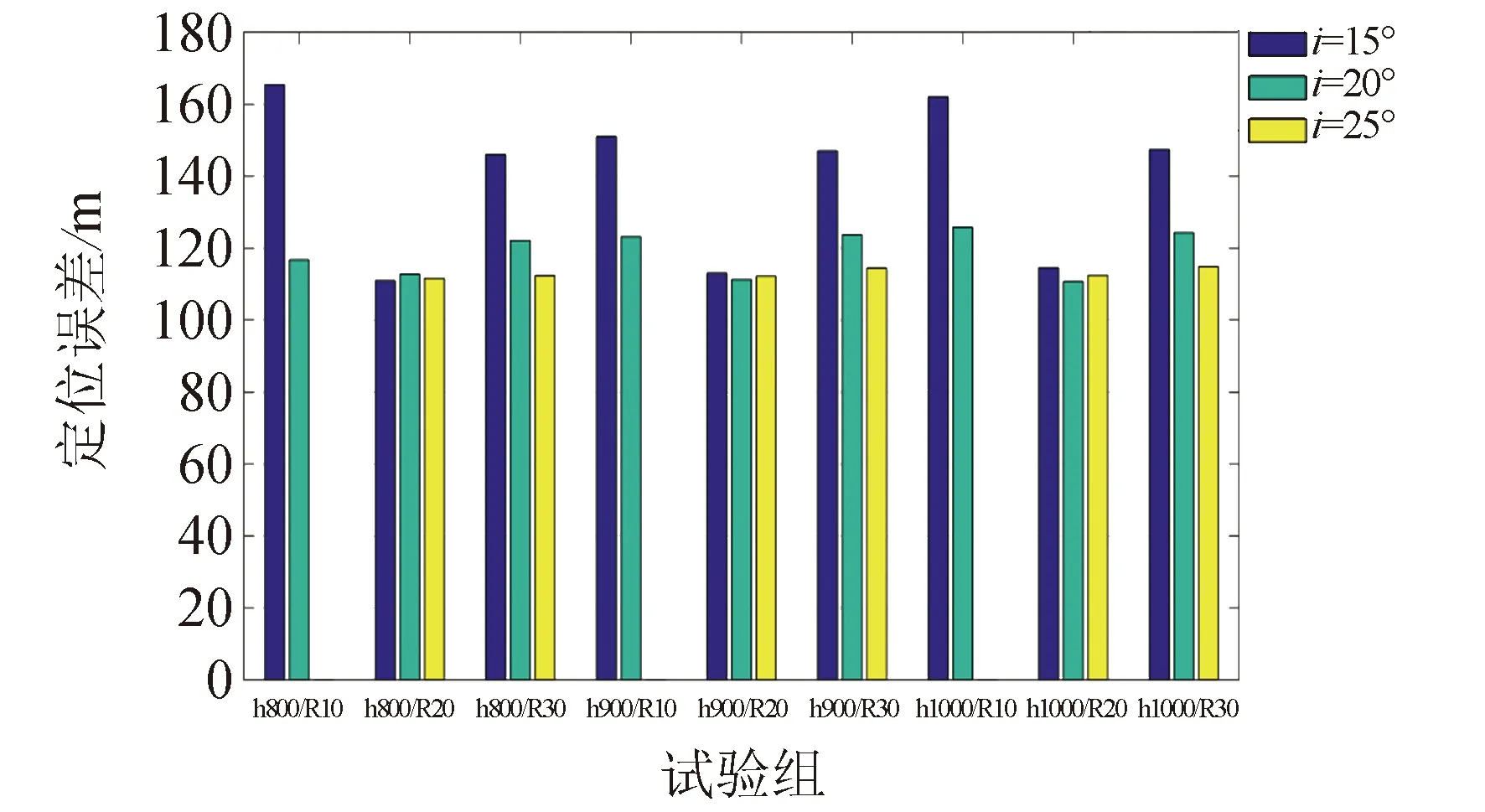
图8 轨道倾角对定位误差的影响 (h800/R10：轨道高度800 km，升交点赤经等差序列10°)Fig.8 Influence of orbital inclination on positioning error (h800/R10:the orbital height is 800 km, the equal difference of RAAN is 10°)

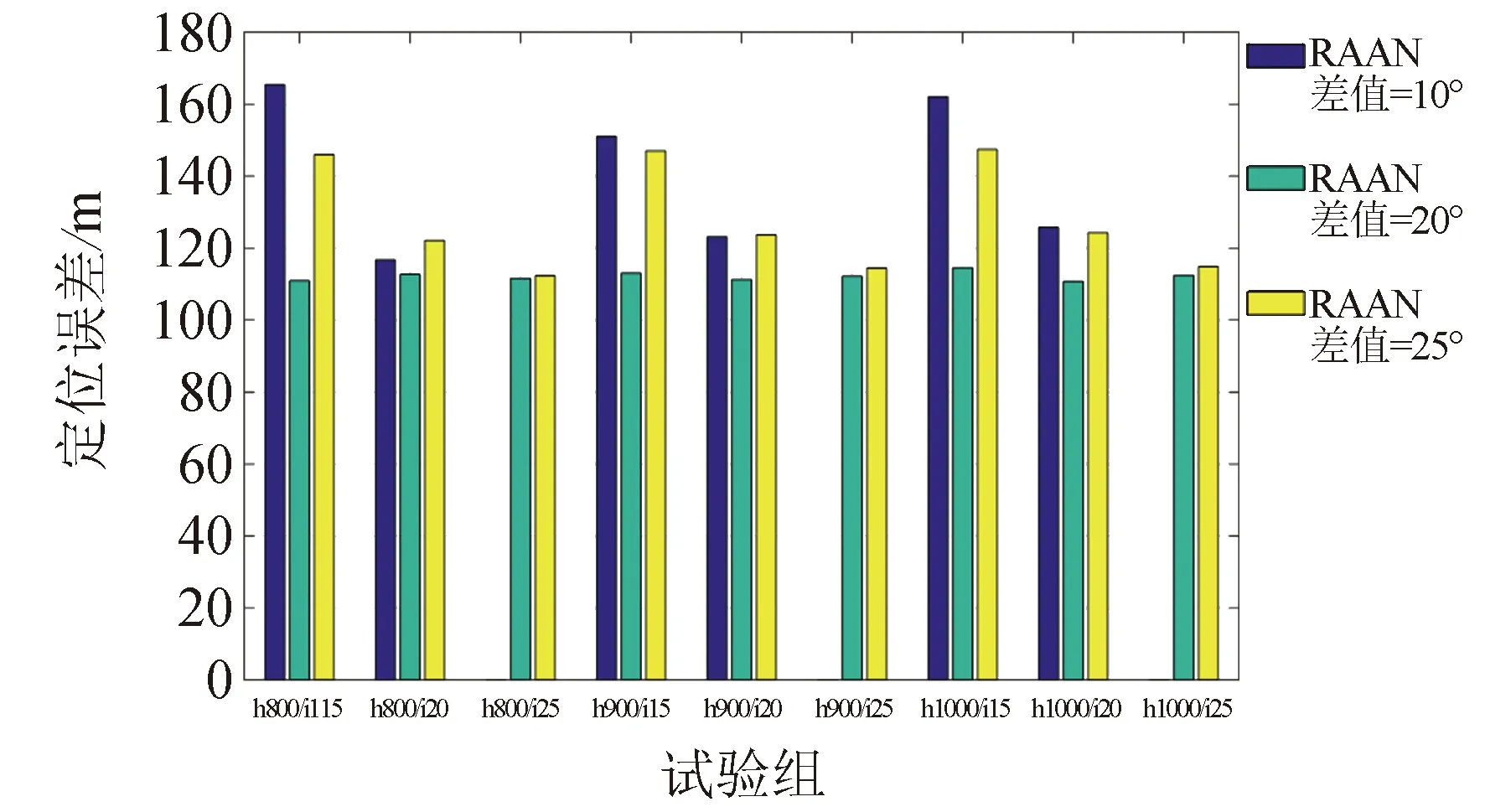
图9 升交点赤经等差序列对定位误差的影响 (h800/i15：轨道高度800 km，轨道倾角15°)Fig.9 Influence of the equal differences of RAAN on positioning error (h800/i15: the orbital height is 800 km, the orbital inclination is 15°)

3 算法应用仿真分析

低轨稀疏星座的对地覆盖情况，特别是对主要服务区域的覆盖完好性、每日服务时长、服务期间定位精度变化和最优定位方案，是星座定位可靠性、完好性的重要指标。本文以水下潜艇为主要服务对象，针对轨道高度900 km，轨道倾角20°，升交点赤经分别为0°、20°和40°，真近点角分别为0°，5°和330°的低轨稀疏星座做进一步仿真分析。

低轨稀疏星座连续运行24 h对地球的覆盖情况如图 10所示，星座长期运行情况下，可以实现对南北纬30°区域的全覆盖。较大的覆盖区域有利于避免敌方通过监测星座的运行轨迹来侦察潜艇位置，更有利于提升潜艇的隐蔽性。单个周期内地面覆盖区域如图 11所示，针对主要服务区域[10°～30°(N)，60°～180°(E)]，即一带一路国家海域及中国东南海域可以实现完全覆盖。

图10 低轨稀疏星座24 h运行轨迹Fig.10 LEO constellation orbit of 24hours

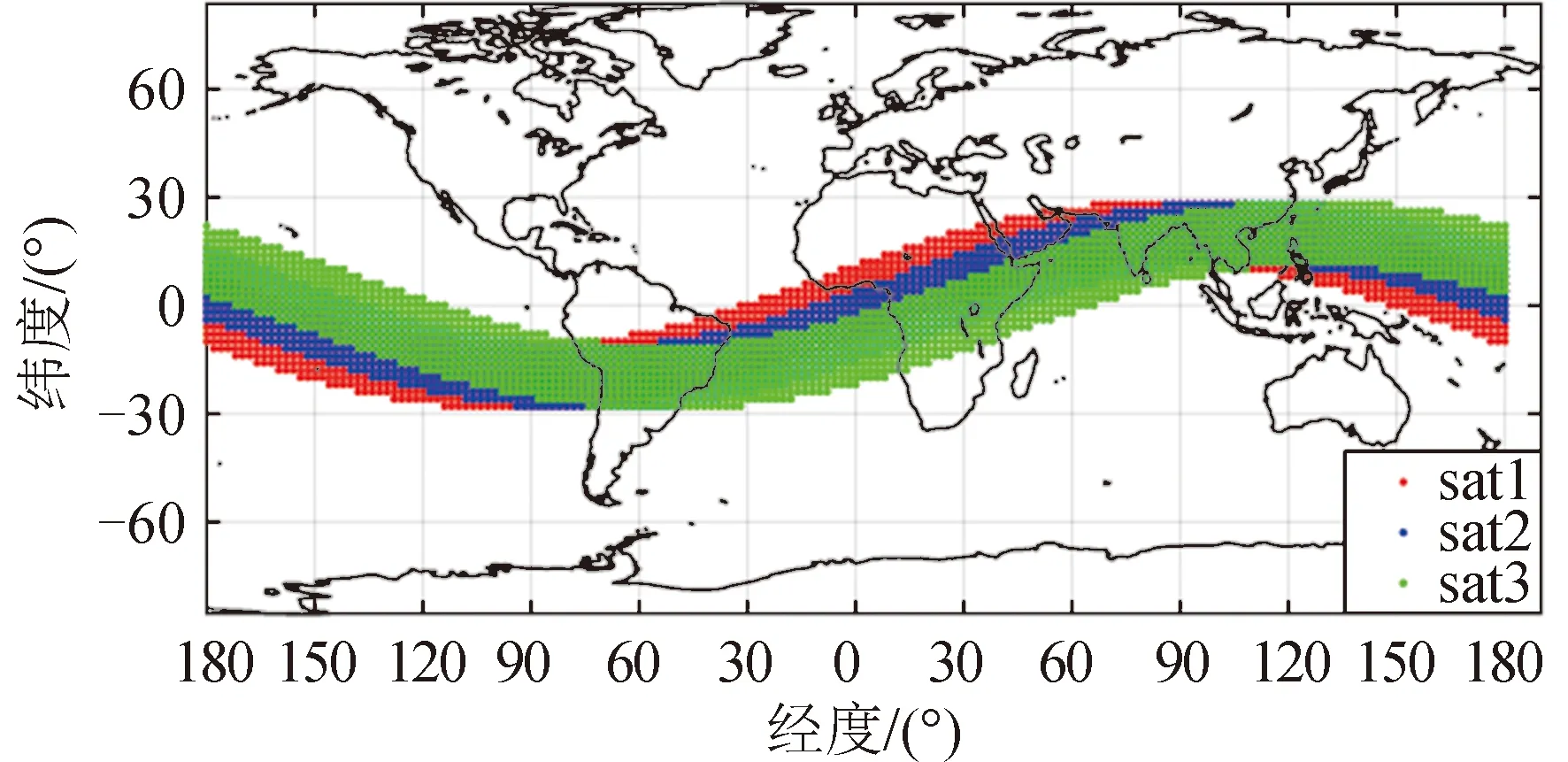
图11 低轨稀疏星座一个周期覆盖区域Fig.11 LEO sparse constellation coverage area

低轨稀疏星座在每天不同时间段，对目标区域的覆盖情况如图 12所示，星座每日过境时间段不同，每日平均覆盖时长约4.6 h，3颗卫星同时覆盖约1.15 h，潜艇在服务区域内可根据星历计算满足定位需求的最优时间段。

低轨稀疏星座过境期间，潜艇可同时与1～3颗卫星进行通信测距，获取伪距观测值，且通信测距采样间隔，将影响卫星与潜艇的几何构型，进而影响定位精度。本文针对仿真目标点为[15°(N)，115°(E)，-100 m]，对低轨星座一次过境全部时段和三颗卫星同时观测时段进行分析。低轨星座从首颗卫星可见到全部过境期间，设伪距观测值采样间隔设为60 s，星座与仿真目标点的PDOP变化情况如图 13所示。变化趋势呈现“倒U型”，星座渐入和渐出段PDOP值变化较大，在5～50之间，定位效果较差，最低段保持在1.5～2.3区间，约持续3～4 min。因此星座过境期间，3颗卫星同时观测时段定位效果最佳。

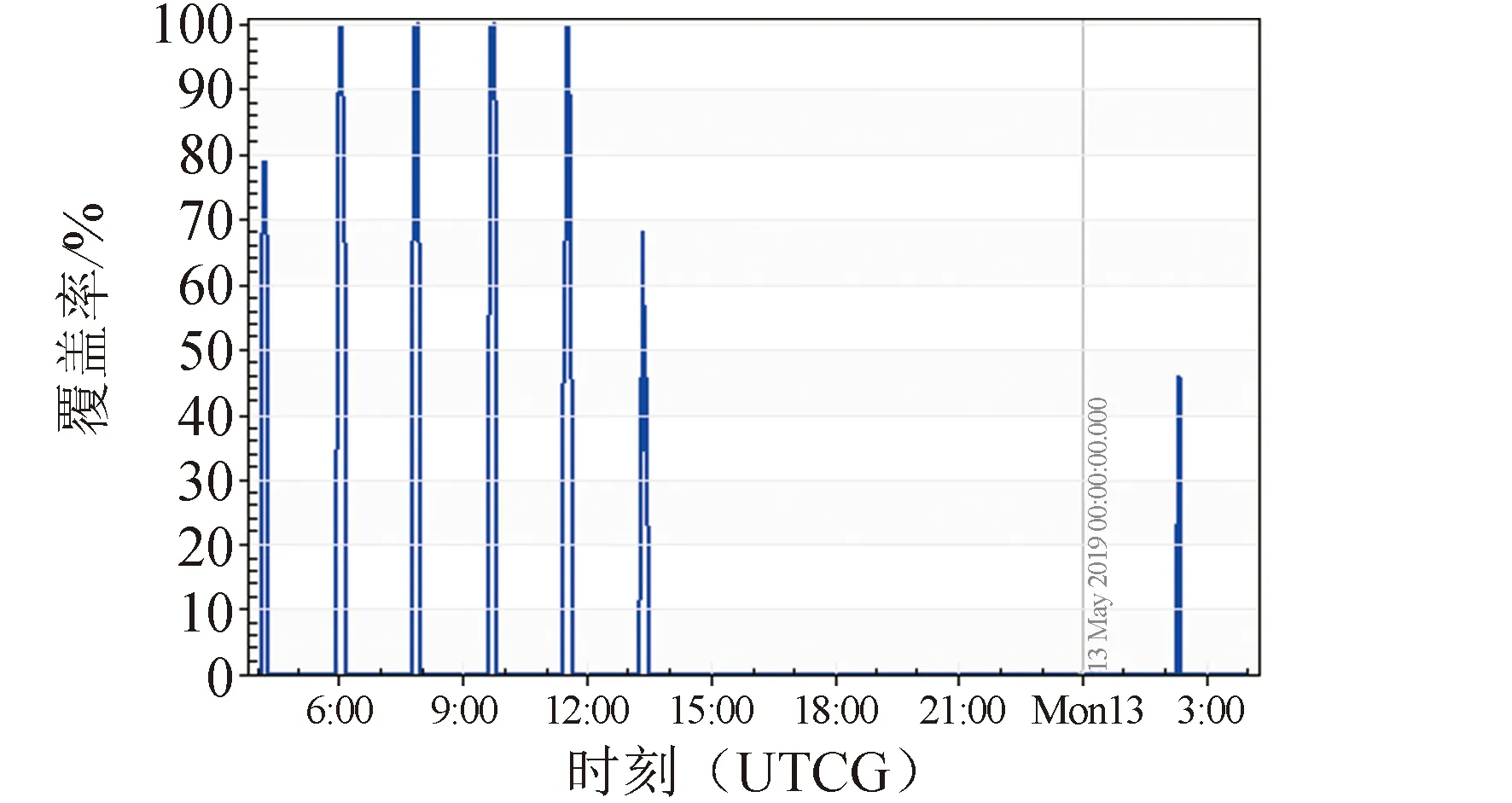
图12 服务区域每日不同时间覆盖情况Fig.12 Service area coverage at different times of the day

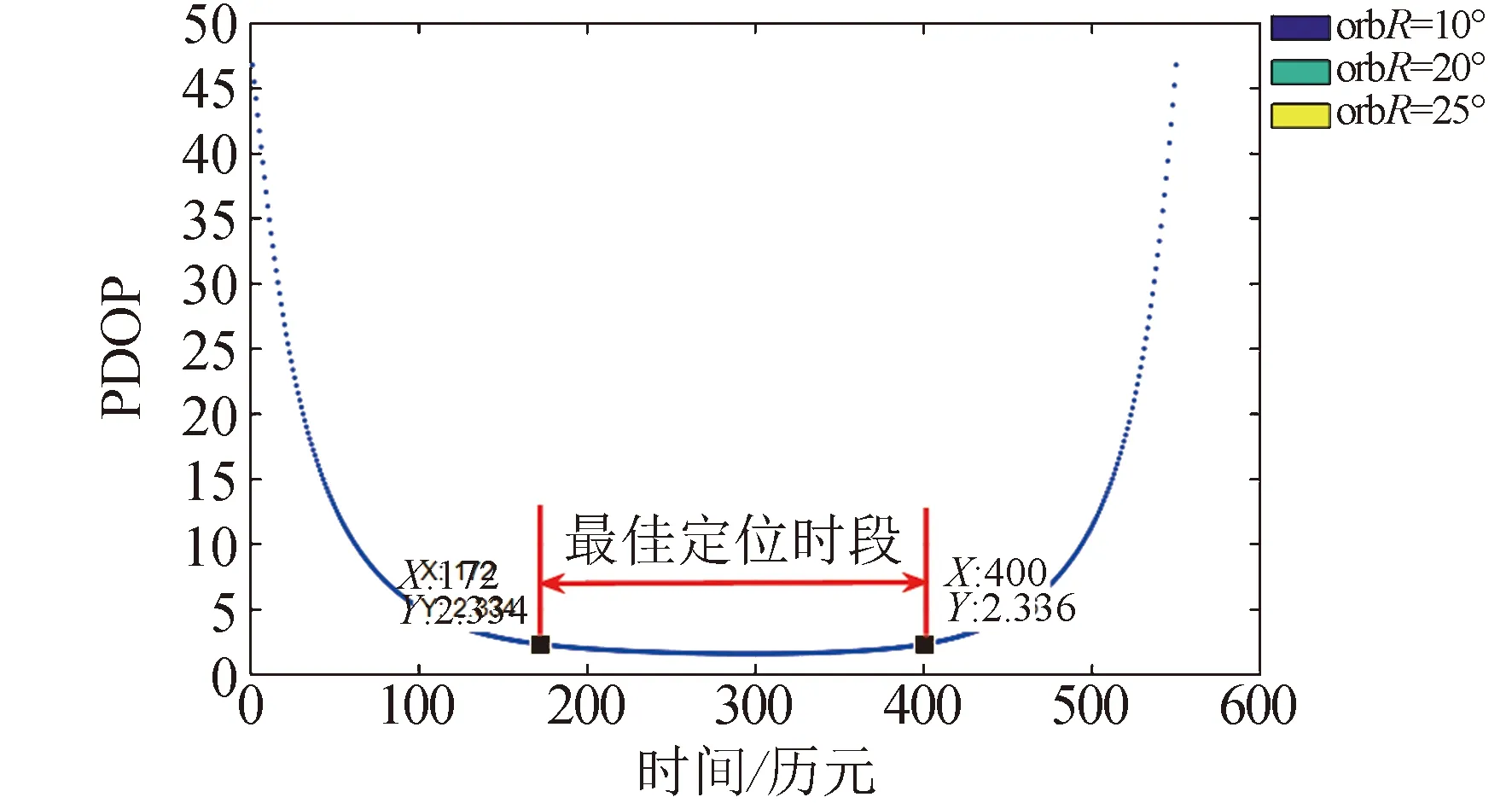
图13星座单次过境期间PDOP变化趋势Fig.13 PDOP changes during constellation single transit

3颗卫星同时过境期间，采样间隔从1～250 s递增，潜艇整体定位精度和PDOP变化情况如图 14所示。随着潜艇通信测距采样间隔递增，PDOP逐渐减小，最终定位误差整体呈现递减趋势。图15表示相同条件下，XY平面和Z方向定位误差的变化趋势。随着观测值采样间隔递增，XY平面误差相对实现大幅度降低，Z方向误差整体影响不大。进一步说明，基于低轨卫星快速运动的特性，增大通信测距采样间隔可以改善星座和潜艇的几何分布，降低PDOP进而提升定位精度。因此潜艇可通过与低轨星座连续多次进行通信测距，采用间隔较大的数据进行定位解算。

图14 不同采样间隔对整体定位精度和PDOP的影响Fig. 14 Influence of different sampling intervals on overall positioning accuracy and PDOP

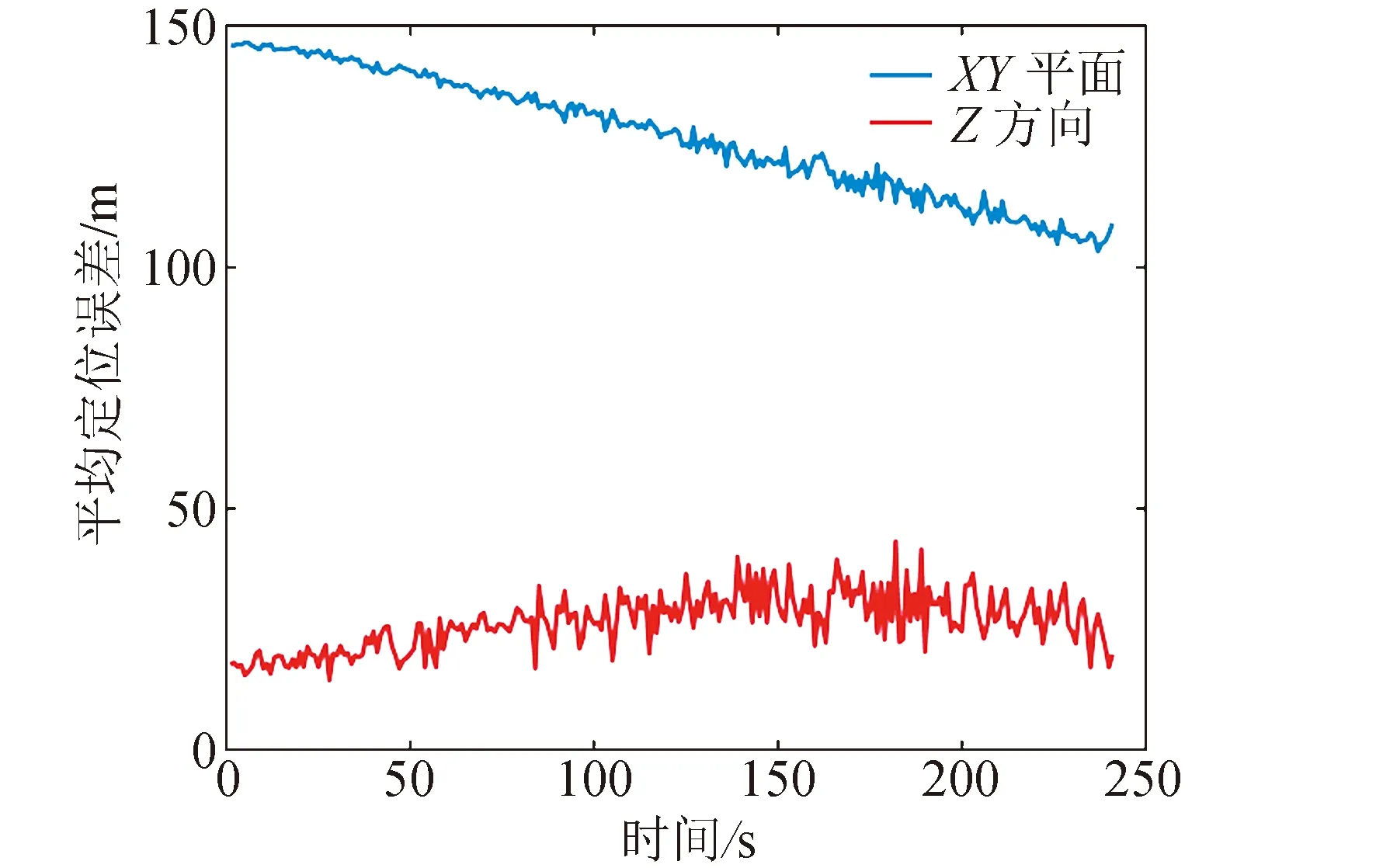
图15 不同采样间隔对XY平面和Z方向定位 精度的影响Fig.15 Influence of different sampling intervals on XY plane and Z direction positioning accuracy

4 结束语

在激光通信测距一体化系统和低轨卫星导航增强精密定轨的研究基础上，本文设计了3颗卫星组成的低轨稀疏星座，利用蓝绿激光实现对潜艇同步完成通信测距，联合高程测量信息实现潜艇水下定位。本文理论分析和仿真验证表明：

1)27种低轨星座的仿真结果表明，轨道构型在一定范围内，最终定位误差将在优于150 m范围，且不同构型差异不大。确认轨道高度900～1 000 km，轨道倾角20°，升交点赤经分别为0°、20°、40°的低轨稀疏星座，具有相对较优的定位效果。

2)联合低轨星座和高程测量信息的水下定位结果显示，3颗卫星可同时观测阶段定位效果最好，每次可持续约3～4 min，且同时观测时段内采样间隔越长定位精度越高。考虑卫星定轨精度，激光在空气、水下传播以及高程测量误差，可实现X、Z方向定位误差优于100 m，Y方向优于150 m。

3)低轨稀疏星座对潜艇导航定位服务性能与星座构型参数、伪距观测值采样间隔、星潜定位几何构型等有关。以我国东南海域为主要服务对象，低轨星座每天过境服务时间约4.6 h，且不同时段覆盖效果不同，潜艇可依据星座星历预测最优过境时间窗口和覆盖区域，从而提升星潜导航定位服务时长和质量。