深空探测航天器巡航段自主导航方法研究
2020-11-30叶子鹏周庆瑞王辉
叶子鹏,周庆瑞,王辉
中国空间技术研究院 钱学森空间技术实验室,北京 100094,中国
21世纪以来,全球各国开始制定火星探测计划,中国拟在2020年实现火星探测。航天器的精确导航将是该计划最为关键的步骤之一。通常情况下,航天器的轨道参数可以通过地面测控站确定或者通过接收GNSS信号自行确定。然而对于深空探测任务,地面测控的方式不仅存在时延问题,对于一些无法在全球布置测控站的国家而言,还存在信号遮挡问题。GNSS则存在覆盖问题、信号强度问题,以及对深空探测航天器的量测几何差。因此,自主导航对航天器提高生存能力、有效完成多项任务具有重大意义。
由于图像处理、敏感器等技术原因,直到1999年,NASA在“新千年计划”中的第一颗探测器“深空一号”才完成了自主导航技术的在轨验证。其方法是利用背景恒星和小行星进行自主导航,导航的位置精度为250 km(3σ),速度精度0.5 m/s(3σ)。随着技术发展,自主导航技术在深空探测中已具有一定的工程可行性,得到了越来越多研究者的关注。由于目前工程上自主导航的精度低于地面测控方式,美国的火星探测任务在巡航段主要采用了地面站测控的方法[1-2],但同时也在大力发展自主导航技术,在多项火星探测任务中开展了天文光学导航的技术验证。随着自主导航技术逐渐成熟,未来的深空探测中自主导航必然会成为主要的导航方法。JPL已经开发了能够实现行星际自主导航(图像处理、轨道确定、机动计算)的软件“AutoNav”[3]。
对于自主导航方法,虽然有学者提出了X射线脉冲星导航[4-6]的方法,但是由于可用脉冲星数量少,且脉冲信号抵达太阳系质心的时间数据库[7]尚未完全建立,脉冲星导航精度无法保证,依然还处于研究阶段。因此深空自主导航目前主要依赖于天文光学测量。Yim等[8]提出了利用航天器相对于太阳的径向速度与航天器同太阳、地球视线矢量相结合的自主导航方法。该方法的仿真精度优于100 km,但是其计算过程中并未考虑动力学模型的噪声,另外对测量精度要求非常高,速度量测精度为cm/s 量级,角度测量精度为亚角秒级,而且航天器与地球的位置有较强的约束。因此该仿真结果不适用于某些深空探测航天器的自主导航。Karimi等[9-10]提出了对量测量的修正方法,对行星视线矢量进行了光时延校正和光像差校正,但是未对滤波算法进行深入研究。
本文提出了一种用于火星巡航段轨道的自主导航方法。该方法首先测量航天器相对于太阳的径向速度,利用扩展卡尔曼滤波估计出航天器状态信息;同时测量多颗小行星的视线矢量,结合最小二乘法估计出航天器位置信息。最后利用一种改进的信息融合算法,对两者的估计值进行有效融合。相比于其他深空探测自主导航方法,该方法对动力学模型精度的依赖度低,位置确定精度高,对于未来的深空探测具有一定借鉴意义。
1 系统状态模型
本文采用的坐标系是J2000日心黄道坐标系,对于导航方案的总体设想如图1所示。

图1 导航方案流程Fig.1 Flow diagram of navigation
令航天器的状态矢量为:
X(k)=[x,y,z,vx,vy,vz]T
(1)
式中:x,y,z分别为航天器三轴位置;vx,vy,vz分别为航天器三轴速度。以太阳为中心引力体的航天器动力学方程表示如下:
式中:r为航天器相对于太阳的矢径,r为向量r的模;v为航天器相对于太阳的速度矢量;μs为太阳引力常数;μi为第i颗行星的引力常数;rip是航天器相对于第i颗行星的矢径;rsi是第i颗行星相对于太阳的矢径;a中包含太阳光压等未建模项。
根据动力学方程,可以将状态模型用下式表示:

式中:f[X(t)]为状态方程;W(t)为过程噪声模型。
2 系统量测模型
2.1 径向速度量测
当航天器相对于某恒星在径向上静止时,接收到的恒星光谱恒定不变。而当航天器存在径向速度时,接收到的恒星光谱将会产生漂移,其漂移量与径向速度成正比。因此可通过测量光谱漂移量来获得航天器相对于某一恒星的径向速度。
分光计基于这一原理,能够达到cm/s量级[8]的径向速度测量精度。因此在进行自主导航研究时,多数学者都选择将径向速度作为确定航天器轨道的量测量。但是只有径向速度作为量测量的模型是不可观的,为了提高自主导航精度,通常还需要加入其他信息量。轨道模型示意如图2所示。
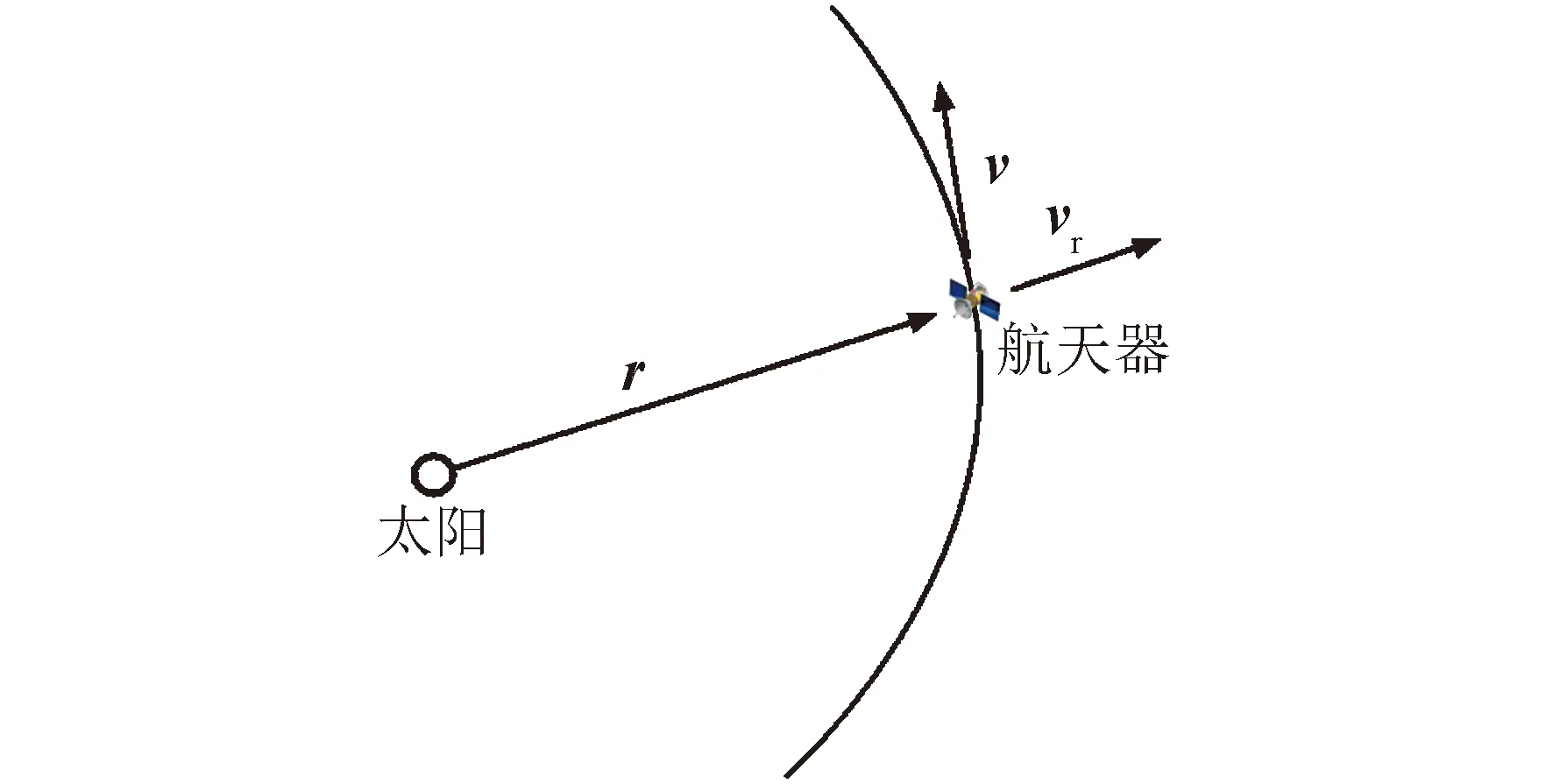
图2 航天器轨道示意Fig.2 Diagram of spacecraft orbit
径向速度的大小vr可以表示为:
量测模型可表示为:
Z(t)=h[X(t)]+V(t)
式中:h[X(t)]为模型量测方程;V(t)为量测噪声。
2.2 小行星视线矢量量测
在巡航段时,小行星带的小行星数量多,距离较地球等大行星离航天器更近,对航天器位置确定的能观度较好。因此选择量测小行星带的小行星视线矢量来确定航天器位置。
星光方向测量多用由镜头光学系统和CCD光敏元件组成的星敏感器来完成,它可以建立如图3所示的测量坐标系。

图3 视线矢量测量模型Fig.3 Diagram of sight vector measurement model
由CCD阵列的测量数据经数据处理可以得到图像中心位置(Px,Py),从而可以得到视线矢量在测量坐标系上的坐标Vp为:

(2)
式中:f为光学系统的焦距。
由已知星敏感器在卫星本体上的安装矩阵M,结合式(2)可得到视线矢量在卫星本体坐标系中的坐标为:
VB=MTVp
式中:M为星敏感器安装矩阵。
通过获取视线矢量在卫星本体坐标系中的方向以及卫星在J2000日心黄道坐标系下的姿态角,就可以求出视线矢量在日心黄道坐标系中的方向。
2.3 系统的可观测度分析
当仅使用径向速度作为量测量时,系统是不可观的。但是结合动力学模型进行卡尔曼滤波时,径向速度的量测可以提高状态估计的精度。
通过测量多颗小行星视线矢量,航天器的位置信息是可观的,利用多个小行星视线矢量可确定航天器的位置。
本文在仿真中对系统的可观测度进行了计算分析。对于线性模型,系统的可观测度计算过程如下:
式中:Φi,k为第k步到第i步的状态转移矩阵;Hi为第i个量测值的量测矩阵;Ri为该量测值的噪声方差阵;n为量测值的维度;W为系统的能观度矩阵,当其非奇异时,系统可观;η为系统的可观测度,系统不可观时为0。对于系统可观测度的分析有助于在小行星星历表中选择合适的小行星进行导航。
由于本文中的量测模型为非线性模型,因此采用的是基于Fisher信息阵[11-13]的系统可观测度分析,令观测向量的概率密度为Pz,同时令量测噪声服从高斯分布,对于一组观测序列:
Z=[Z1,Z2,…,Zk]T
其中Z1,Z2,…,Zk分别为各量测量。其概率密度Pz(Z|x)的对数表示形式为:
lnLx(Z)=ln[Pz(Z|x)]=

根据Fisher信息阵计算方法得信息阵:
式中:X为对象状态信息。根据Cramer-Rao不等式,估计均方误差阵P有:
P≥J-1
因此,可以用信息阵的逆来估计可观测度,其表达形式为:
式中:J为信息阵。
对选择不同数量导航小行星的模型可观度进行计算,得到结果如图4所示。
图4中系统可观测度大于0,说明系统的状态是可观测的。同时通过观察可观测度变化的规律可以得到,选择的导航星数越多,系统可观性越好。
在选择相同数量的导航小行星时,可观测度的上下波动可以反映航天器与导航小行星之间的距离变化:可观测度越高,航天器与导航小行星之间的距离越近;可观测度越低,航天器与导航小行星之间的距离越远。
选择不同星数的最小二乘滤波结果的误差平滑后如图5所示。
根据图4与图5,可以得到在利用较少数量导航小行星的情形下,当可观度下降时,滤波误差呈现上升趋势;当可观度上升时,滤波误差呈现下降趋势。
同时可以得到,随着导航小行星数量增加,系统可观测度上升,滤波误差下降。但是当导航小行星数提升至12颗以后,滤波精度提升不大。综合考虑航天器的量测代价,故选择导航小行星数量为12颗。

图4 不同数量导航小行星的系统可观度Fig.4 Observability with different number of navigation asteroids
3 滤波算法
3.1 扩展卡尔曼滤波
扩展卡尔曼滤波方法计算简便,而且可以获得较好的滤波结果,广泛应用于航天器自主导航中。因此本文采用扩展卡尔曼滤波对航天器状态进行估计,离散的状态模型可以简单化地表示如下:
X(k)=f[X(k-1)]+W(k-1)
式中:X(k)如式(1)所示;W(k)为过程噪声;V(k)为量测噪声。令:
E[W(k)W(k+i)T]=Q(k)δ(i)
E[V(k)V(k+i)T]=R(k)δ(i)
式中:Q,R分别为过程噪声与量测噪声的均方差阵。当且仅当i=0时,δ(i)为单位阵,否则为0矩阵。
则扩展卡尔曼滤波过程如下所示:

3.2 最小二乘法
最小二乘法的优点是方法简单,使用过程中不需要任何先验的状态信息,也不需要动力学模型的参与,因此可以避免因动力学模型不准确而造成滤波误差的问题。同时,最小二乘法得到的位置精度会随导航小行星数量的增加而提高,而小行星带恰好能够提供足够数量的导航小行星,并且当航天器越靠近小行星,自主导航的精度会越高。最小二乘法小行星视线矢量的分布如图6所示。
对于小行星的矢量距离Sn有:
Sn=lnρn
式中:ln为第n颗小行星的视线矢量;ρn为航天器同第n颗小行星的标量距离。可以得到如下等式:
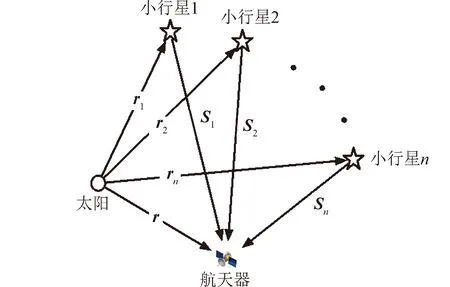
图6 小行星量测示意Fig.6 Diagram of asteroid measurement
r=r1+l1ρ1=r2+l2ρ2=…=rn+lnρn
(3)
式中:l1到ln为量测的视线矢量,其形式为3维的列向量;r1到rn可通过查询小行星的星历表获取,均为3维的列向量。小行星的星历误差通常为100 km(3σ),在仿真中设置小行星视线矢量量测误差为角秒级时,可以满足仿真过程中所需的星历误差条件。根据式(3)可以建立如下方程:
一是现行法律规定不明导致诉讼主体不清。民事诉讼法将公益诉讼主体限定在“法律规定的机关和有关组织”,但未对其具体范围作出明确规定。在水资源保护公益诉讼领域,“法律规定的机关”是否包括水行政主管部门,抑或还包括其他机关,尚须进一步明确;至于“有关组织”,其范围更加广泛,是仅指所有在民政部门登记的组织(合法社会组织),还是指须经相关法律特别授权的社会组织,目前也不明确。此外,“法律规定的机关”和“其他组织”之间的诉权顺序,目前也缺乏规定。

(4)
ri可视作已知量,故式(4)可表示为:
li=hi(r)
基于递推最小二乘算法,状态r的迭代可用算法中的X等价表示,计算过程如下:
式中:Wk+1为量测量的权重系数;Hk+1为
由于量测方程存在线性化误差,仿真试验发现,通过递推最小二乘法所得结果的精度略差于通过下式批处理法所求结果的精度:

(5)
式中:I3×3为3阶单位阵。对于不相容的方程:
Ax=b
式(5)中有3n个方程,需要解得n+3个解,当n≥2时,存在矩阵A列满秩,则有最小二乘解:
x=(ATA)-1ATb
(6)
利用式(6)即可得到航天器位置信息的最小二乘解。
3.3 信息融合

(7)
式中:
βi(k)为两种估计值的权重;P1(k)为扩展卡尔曼滤波在第k步估计后的均方误差阵;P2(k)为最小二乘估计均方误差阵,由于在本文所仿真的场景中最小二乘估计所得误差变化不大,因此可以将其设置为一个不变的矩阵。本文仿真中将P2(k)的2-范数值设置为 106~107之间的固定值,该值大约为最小二乘估计所得位置误差的平方值。若是P2(k)变化较大,则可以用最小二乘估计均方差阵的迭代算法进行计算。

4 仿真试验
4.1 仿真条件
导航小行星的选择方法来源于文献[14],小行星的星历数据来源于JPL的HORIZONS System。
相关学者对深空探测转移轨道[15-16]进行了深入研究,本文采用的火星巡航段轨道是双切轨道,考虑在J2000日心黄道坐标系下航天器Z轴状态分量较小,为简化计算,只考虑X、Y轴的位置和速度状态信息。由于初始的位置误差不影响最终的滤波结果,多数相关文献的仿真试验中将其设置为几十到几百千米,因此本文将其设置为500 km,并且将速度误差设置为0.01 km/s,径向速度量测误差设为10-5km /s,小行星的视线矢量量测误差设为4″(3σ) 。当选择滤波周期过短,不仅会占用过多星上资源,而且相邻两步中量测量变化过小,甚至被量测噪声覆盖;当滤波周期过长,仿真精度下降。文献[9]中将滤波周期设置为50 min左右,为了便于比较,本文设置仿真中的滤波周期为3 600 s,仿真总时长大约为140 d。
4.2 仿真结果
计算可以得到太阳对火星巡航段航天器的加速度为10-6km/s2量级,航天器在火星巡航段受到扰动总和约为10-10km/s2量级,因此对动力学模型添加10-9km/s2量级的噪声。
最小二乘法的位置估计结果如图5所示。单独以径向速度值为量测量进行卡尔曼滤波的结果如图7所示,信息融合的滤波结果如图8所示。
由于单独以径向速度值作为量测量的系统是不可观的,因此图7中位置估计误差无法收敛至0附近。而多次仿真证明,仅使用该方法时最终收敛到的结果是一个无法预测的数值。
由图8可以看出,信息融合滤波结果中位置估计误差在80 km以内,远优于单独使用最小二乘法和卡尔曼滤波的结果。速度估计精度优于1.2×10-4km/s,与单独使用卡尔曼滤波的结果相近。
我们也分别做了提高小行星视线矢量与径向速度量测精度的仿真试验,都得到了更高精度的试验结果。

图7 卡尔曼滤波结果Fig.7 Results of Kalman filtering

图8 信息融合滤波结果Fig.8 Results of information fusion filtering
5 结束语
本文对深空探测航天器巡航段的自主导航方法开展了研究,提出了一种结合相对太阳径向速度测量与小行星视线测量的导航方法和数据融合算法。在理论上分析了系统的能观性,定量计算了能观度,给出了小行星的选取建议。以实际工程可行的量测精度和动力学模型精度为输入条件,开展了仿真分析,结果表明位置估计误差为80 km(3σ),速度估计误差为0.12 m/s(3σ)。该方法计算简单,精度可满足巡航段的工程需求,具有很强的实用性。本文只对导航小行星提出了部分选取建议,对于具体的导航小行星选择未做深入研究,该方面研究将作为本课题的未来工作展开。
