基于跟瞄和加表PI滤波近程相对导航方法

王献忠，张 肖，张丽敏，施常勇

(1.上海航天技术研究院，上海 201109； 2.上海航天控制技术研究所，上海 201109； 3.上海市空间智能控制技术重点实验室，上海 201109)

0 引言

近程相对导航是空间飞行器交会的关键技术。与非合作目标进行交会时，空间飞行器因不能与目标进行通信而无法获取目标精确的导航定位信息。因此，国内外学者对近程相对导航进行了广泛研究。从公开文献来看，大部分采用了卡尔曼滤波技术或其衍生算法。文献[1-4]介绍了基于扩展卡尔曼滤波技术的激光雷达和惯导的非合作目标相对导航技术，其中，文献[1-3]将导航算法建立在惯性坐标系下，文献[4]将导航算法建立在当地水平垂直坐标系下。文献[5-6]提出了一种光学敏感器加惯导的航天器组合相对导航方法，并在此基础上设计了卡尔曼滤波器。文献[7-8]基于模糊迭代均方根容积卡尔曼滤波算法研究非合作目标的相对导航算法，但其重点是将采用扩展卡尔曼滤波、容积卡尔曼滤波，以及模糊迭代均方根容积卡尔曼滤波的算法进行仿真对比，未与工程实际相结合，算法坐标系被建立在站心赤道坐标系下。上述文献均采用了比较复杂的滤波算法，且都未关注对加表漂移的估计效果。对比上述文献，本文提出的基于跟瞄和加表比例积分(PI)滤波的近程相对导航技术将坐标系建立在轨道坐标系下，有利于控制，且相对于卡尔曼滤波和更高阶的滤波而言，算法更为简单。

本文研究了基于PI滤波估计加表漂移的跟瞄近程相对导航算法。首先推导了基于C-W(Clohessey-Whiltshire)方程的近程相对导航算法，并基于相对导航与跟瞄输出计算的相对位置/相对速度误差和PI滤波估计加表的加速度漂移；然后给出了基于相对位置/相对速度，以及仅基于相对位置信息的跟瞄与加表近程相对导航算法；最后进行了工程应用方式分析和仿真验证。

1 基于C-W方程的近程相对导航算法原理

近距离跟踪时，两星轨道坐标系基本一致，轨道角速率也基本一致。考虑到目标星轨道一般未知，基于跟踪星轨道系进行近程相对导航，并用跟踪星轨道角速率代替目标星轨道角速率。

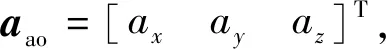
aao=Aoa·aaa

(1)

式中：aaa为加表测得的加表坐标系下的非惯性加速度。

(2)

(3)

式中：n为跟踪星轨道角速度；μ为地球引力常数；a为跟踪星轨道半长轴；ax，ay，az为跟踪星在跟踪星轨道系下的非惯性加速度。

ao为跟踪星轨道系下两星相对加速度，则

(4)

在跟踪星轨道系下进行近程相对导航解算，求得相对速度vo和相对位置ro为

(5)

(6)

式中：t为时间。

2 基于跟瞄和PI滤波近程相对导航算法

2.1 相对位置/相对速度误差和加表漂移估计

近程相对导航一般基于C-W方程推算相对位置和相对速度。近距离跟踪时，两星惯性加速度基本一致。目标星非惯性加速度一般不可获得，跟踪星配置的加表虽能连续输出推力等非惯性力产生的加速度，但加表输出加速度存在漂移。这会导致长时间基于C-W方程递推时，两星相对位置和相对速度误差逐步增大。因此，需要利用能测量相对信息的光电组合、微波雷达、激光雷达等跟瞄敏感器，对相对位置和相对速度进行修正。

跟瞄可能受单粒子翻转、姿态机动或翻滚时失捕目标、地面局部区域人为干扰等影响，特别是在跟瞄复位或重加载期间，跟瞄不能连续输出两星相对测量信息。因此，相对导航输出仍为C-W方程递推结果，跟瞄有效时，基于跟瞄信息对C-W方程递推的相对位置和相对速度误差进行估计并修正。该方式既可确保相对位置和相对速度输出的连续性，又可抑制跟瞄观测噪声对近程相对导航精度的影响。目前已有的卡尔曼滤波算法比较复杂，不利于在轨实现。本文提出的PI滤波估计方法不涉及多阶矩阵求逆及其他计算，滤波参数由地面设计，算法简单可靠，适合于在轨应用。

图1为跟瞄测量示意图。图中：A为目标星；T为跟踪星；α为两星相对位置矢量在跟踪星轨道坐标系XoYo面的投影与Xo的夹角，为跟瞄输出的方位角；β为投影与两星相对位置矢量的夹角，为跟瞄输出的高低角。

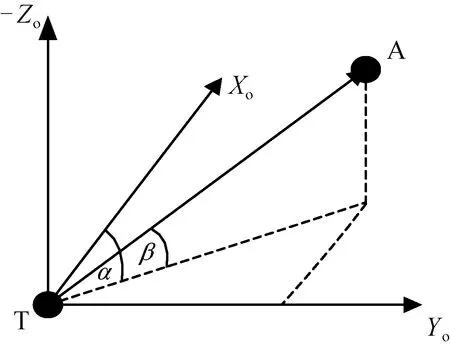
图1 跟瞄测量示意图Fig.1 Schematic diagram of tracking and pointing measurement

跟踪星相对目标星的位置为

xTtoA=-ρ·cosβ·cosα

(7)

yTtoA=-ρ·cosβ·sinα

(8)

zTtoA=ρ·sinβ

(9)

式中：ρ为跟瞄输出的视线距。

基于跟瞄视线距变化率和视线角变化率，求得相对速度为

(10)

(11)

(12)

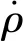
设加表加速度漂移转换到跟踪星轨道系为δao，求得加表漂移引起的相对速度误差δvo和相对位置误差δro为

(13)

(14)

设基于跟瞄解算输出的相对位置roT和相对速度voT为

(15)

(16)

基于近程相对导航第k步解算输出的相对位置ro,k和相对速度vo,k，求得近程相对导航解算引起的相对位置误差Δro,k和相对速度误差Δvo,k为

Δro,k=ro,k-roT

(17)

Δvo,k=vo,k-voT

(18)

基于跟瞄求得近程相对导航相对位置误差Δro,k和相对速度误差Δvo,k。在近程相对导航积分过程中，逐步增加相对位置和相对速度误差修正量，可确保误差修正的平稳性。第k步近程相对导航解算相对位置误差修正量rdo,k和相对速度误差修正量vdo,k为

rdo,k=kpr·Δro,k

(19)

vdo,k=kpv·Δvo,k

(20)

式中：kpr，kpv分别为三轴相对位置和相对速度误差修正量估计比例系数。kpr，kpv为3×3对角阵，三轴可独立估计相对位置和相对速度误差修正量。

将跟瞄求得的近程相对导航相对速度误差Δvo,k转换到加表坐标系，即

Δva,k=Aao·Δvo,k

(21)

式中：Aao为跟踪星轨道系到加表坐标系的姿态转换矩阵；Δva,k为加表坐标系下相对速度误差。

基于PI滤波估计加表加速度漂移算法为

(22)

式中：δaa,k为第k步估计的加表漂移；kpa，kia分别为三轴加速度漂移估计比例系数和积分系数。kpa，kia为3×3对角阵，三轴可独立估计加速度漂移。kpa影响滤波收敛速度，取值范围一般为0.01～0.1；kia影响滤波收敛精度，取值通常比比例系数低一个数量级。

2.2 跟瞄与加表近程相对导航

设加表加速度漂移估计为δaa，求得跟踪星轨道系下扣除加表漂移的跟踪星非惯性加速度

aao=Aoa·(aaa-δaa)

(23)

式中：Aoa为加表坐标系到跟踪星轨道系的姿态转换矩阵。

求得跟踪星轨道系下，扣除加表漂移的两星相对运动加速度

(24)

在跟踪星轨道系下，扣除相对位置和相对速度误差修正量，应用简化积分算法进行近程相对导航解算，即

vo,k=vo,k-1+[ao,k-1+

ao,k-ao,k-1/2]·T-vdo,k-1

(25)

ro,k=ro,k-1+[vo,k-1+

vo,k-vo,k-1/2]·T-rdo,k-1

(26)

式中：ao,k-1为第k-1步扣除加表漂移的加速度；ao,k为第k步扣除加表漂移的加速度；vdo,k-1为第k-1步估计的相对速度误差修正量；vo,k-1为第k-1步扣除相对速度误差修正量的相对速度；vo,k为第k步扣除相对速度误差修正量的相对速度；rdo,k-1为第k-1步估计的相对位置误差修正量；ro,k-1为第k-1步扣除相对位置误差修正量的相对位置；ro,k为第k步扣除相对位置误差修正量的相对位置；T为相对导航周期。

3 工程应用

3.1 基于相对位置/相对速度估计

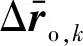
(27)

(28)

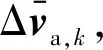
(29)

3.2 基于相对位置估计

跟瞄输出的相对速度精度远低于相对位置精度，且观测噪声较大。为防止低精度的相对速度观测量影响近程相对导航精度，实际工程应用中，可仅基于跟瞄输出的相对位置与加表进行近程相对导航。

考虑到相对位置误差也能反映相对速度误差，基于相对位置误差修正量rdo,k估计相对速度误差修正量。

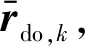
(30)

将相对速度误差修正量vdo,k转换到加表坐标系，即

vda,k=Aao·vdo,k

(31)

4 仿真验证

加表三轴加速度常值漂移分别为-0.005，0.002，0.006 m/s2，随机漂移为0.000 5 m/s2，跟瞄视线距常值误差为15 m，视线角偏差为0.1°。仿真中比例和积分系数取值为0.03/0.001。

利用跟瞄输出的视线距和视线角计算两星相对位置，再与加表基于PI滤波进行近程相对导航仿真。其中，加表加速度漂移估计仿真结果如图2，3所示，跟瞄与加表近程相对导航收敛后相对位置和相对速度误差仿真结果如图4，5所示。

图2 基于相对位置观测信息加表加速度漂移估计曲线Fig.2 Estimation of acceleration drift based on relative position observation information

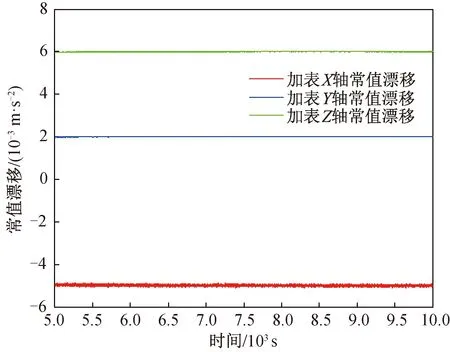
图3 基于相对位置观测信息加表加速度漂移估计放大Fig.3 Amplification curve of acceleration drift estimation based on relative position observation information

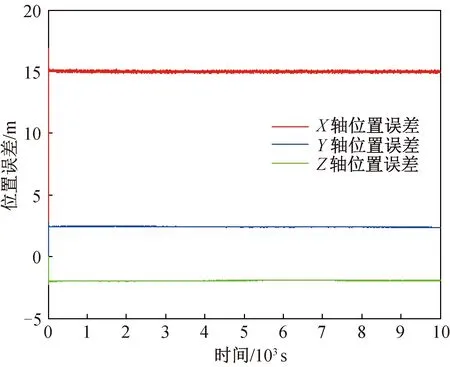
图4 基于相对位置观测信息组合导航位置误差曲线Fig.4 Position error of integrated navigation based on relative position observation information

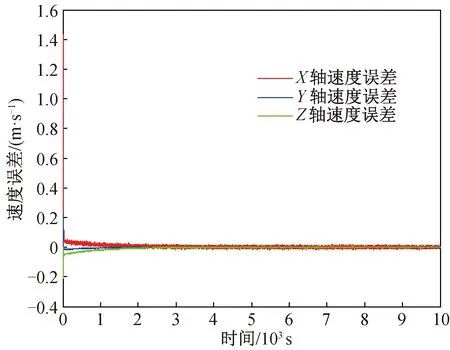
图5 基于相对位置观测信息组合导航速度误差曲线Fig.5 Velocity error of integrated navigation based on relative position observation information

由图可知：以仅基于跟瞄的相对位置作为观测量时，加表的常值漂移也能被准确估计，估计精度小于0.000 5 m/s2，相对位置误差小于20 m，相对速度误差小于0.05 m/s。

5 结束语

本文在PI滤波估计加表加速度漂移的基础上，进行了跟瞄与加表近程相对导航算法研究，通过仿真验证了近程相对导航算法的有效性。基于PI滤波估计加表漂移的跟瞄与加表近程相对导航方法计算简单，易于工程实现，且已通过在轨考核验证。本研究选用的目标飞行器为一稳定目标，后续可针对旋转或机动目标飞行器探测和近程相对导航算法适应性做进一步研究。