盾构隧道与隐伏溶洞的安全距离研究

赵勇

盾构隧道与隐伏溶洞的安全距离研究

赵勇

(中铁南方投资集团有限公司, 广东 深圳, 518000)

为解决隧道盾构施工遇到隐伏溶洞时的安全距离的确定问题, 通过弹性力学的相关理论对盾构隧道与隐伏溶洞之间的安全距离进行研究, 应用突变理论建立盾构施工时的隐伏溶洞与掌子面间关于安全距离计算或预测的非线性—尖点突变模型, 通过深入探索与研究多种空间状态与盾构隧道掌子面对安全距离因素产生的影响, 与深圳地铁14号线大运至宝荷工程区段中岩溶区盾构隧道工程项目相结合进行研究与分析。结果表明: 在计算各种空间状态与盾构隧道间下隐伏溶洞安全距离时, 运用尖点突变模型方式取得的结果更精准, 可以更好应用于实践, 有效地指导隧道工程的建设。

盾构隧道; 隐伏溶洞; 安全距离; 突变理论; 岩溶区

岩溶区盾构隧道在施工中遇到多因素的不利影响, 主要包括溶洞填充物、周围溶洞、突泥、突水等对施工的影响。盾构施工的通常情况下会根据工程实际需要预留出一定的岩墙厚度, 从而可有效减少液态填充物压力上升而压溃岩墙, 造成突发性的安全问题。同时, 若岩墙厚度过小, 将导致溶腔与岩墙之间在高压下出现岩体压溃现象, 十分不利于爆破泄水和注浆加固等阶段的施工过程, 势必提升工程建设的风险和成本[1]。因此, 为有效计算或预测出溶洞与盾构隧道间的安全距离, 国内外学者以定性、半定量等分析方式做出了大量的研究, 且已取得了重大的研究成果, 高峰等[2]通过建立有限元数值模型和反复多次模拟计算得出了不同影响因素组合下顶板的安全厚度值。并进一步利用多元逐步回归分析方法建立了一能够综合反映多因素共同作用下的复杂充填体下矿体开采安全顶板厚度的数学预测模型; 王勇等[3]利用支持向量机方法得出了能综合体现各影响因素的溶洞顶板安全厚度预测模型, 并和多元线性回归得到的预测模型进行对比, 验证了支持向量机预测模型具有更高预测精度的结论; 林杭等[4]借鉴强度折减法计算边坡安全系数的思路, 提出了采空区安全顶板预测的厚度折减法; 宋战平等[5]采用弹性梁、板理论, 对不同力学模型的受力状态进行分析, 提出了建立在岩体技抗拉和抗剪强度准则基础上的岩溶隧道底板岩层的最小安全厚度分析公式; 刘超群等[6]通过数值模拟和理论计算, 对隧道掌子面与溶洞安全距离的影响因素进行了分析研究, 建立了预测隧道掌子面前方岩盘安全厚度的计算方法(经验类比法、理论计算法、数值分析法)及计算图式, 得到了安全距离计算公式; 张梅等[7]对多种不同影响因素深入分析后运用剪切破坏理论计算得出最小安全岩盘厚度; 赖永标[8]提出了基于突变理论隐伏溶洞与隧道间安全距离研究方法, 采用突变理论评价隐伏溶洞与隧道间岩层的稳定性, 通过研究隐伏溶洞与隧道间岩层系统的总势能, 建立岩层系统失稳的突变模型, 分别推导出了隧道顶部隐伏溶洞、底部隐伏溶洞和前方隐伏溶洞时岩层突变失稳判据、失稳力学条件和安全距离的计算公式。但大多数计算盾构隧道与溶洞间安全距离的公式没有考虑势能积聚的影响, 尤其当溶洞为隐伏溶洞时, 岩墙被压溃过程是一个弹性势能的积聚过程, 岩墙弯曲变形时会积聚大量能量, 当势能积累到一定程度后会影响岩墙的稳定性, 造成岩墙失稳, 甚至发生压溃现象[8]。同时, 目前现有研究成果大多针对正常情况下的溶洞与盾构隧道间的安全距离进行的研究, 重点针对隐伏溶洞与盾构隧道间的安全距离研究的相关成果仍相对较少。

基于此, 本文综合考虑岩墙系统的势能影响, 采用突变理论建立隐伏溶洞与盾构隧道间安全距离的计算模型, 并根据溶洞与掌子面间的正交、斜交2种不同时空关系进一步完善计算模型的表达式, 得到可以用于工程实践的盾构隧道与隐伏溶洞之间的安全距离计算的模型表达式, 为类似工程的建设提供理论指导和参考。

1 基于突变理论的分析模型

1.1 突变理论

突变理论属于基于拓扑学的结构稳定性理论, 可用它来判断突变发生的状态。该理论通过多种形式微分方程及控制变量来预测系统的状态[9]。目前尖点突变理论模型作为突变理论模型的典型代表, 在实际工程中广泛运用, 基本原理是由两个稳定点与一个不平衡点持续进行平衡状态演化, 位于某个拐点位置出现突变而构建的一种新平衡突变理论模型, 本模型可以在研究岩梁墙系统临界失稳破坏过程中使用。

1.2 非线性—尖点突变模型的建立

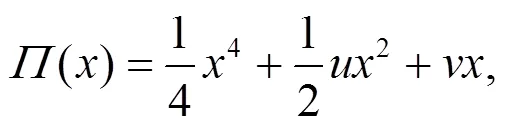
三维空间(,,)中该模型为褶皱曲面, 各个区域中平衡位置分别为1、2或者3个。势函数对应于褶皱曲面上叶与下叶平衡位置, 保持稳定状态。曲面中具有竖直切线, 平衡曲面中2条相互垂直切线的点集S方程式为

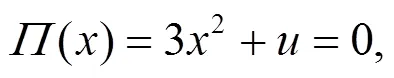
式(1)中极值点左侧与右侧平衡位置数量不同, 该极值点被称作奇异点或者突变点, 其本质为曲线(曲线为抛物线具有参数(u, x)上的拐点, 如图1所示[13]。系统特征通过光滑势函数深入分析, 本状态曲面由3部分构成: 上叶、中叶、下叶, 由正面对图形分析, 该图与S形曲线相似, 并在图中表现出显著的拐点。假设由x、u、v作为三维相空间坐标, 其中任意一点表示系统状态, 所有相点最终全部在三叶曲面上。改变系统参数后平衡位置成为突变流形上的曲线(见图2), 经过分析后即可得出曲线特征: ①多模态; ②跳跃性; ③滞后性; ④不可及性; ⑤发散性。

在参数空间经过作用后生成分叉集, 由△ = 83+ 272= 0来表示, 图2为分叉集—尖点突变理论模型。

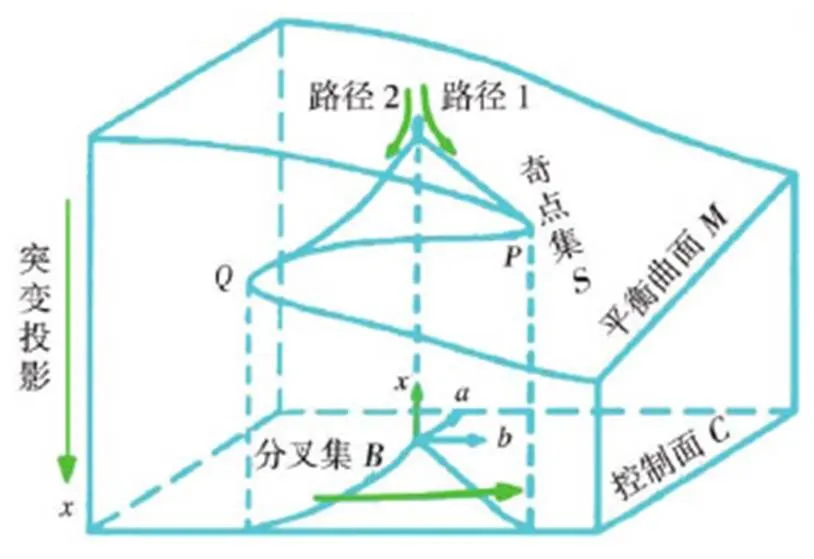
图2 分叉集—尖点突变理论模型示意图

2 基于尖点突变理论安全距离分析

基于尖点突变理论对安全距离进行分析时, 根据溶洞与掌子面之间的空间状态进行分类, 分为溶洞与掌子面斜交以及溶洞与掌子面正交2种情况加以讨论研究。其中, 溶洞与掌子面斜交的位置情况较复杂, 即溶洞斜交于隧道的掌子面位置处且在隧道附近任意位置上都会存在该情况, 此时溶洞的跨度一般较大; 溶洞与掌子面正交的位置情况较简单, 即溶洞处于隧道的掌子面上, 此时溶洞的跨度较小, 可以将其视作中小跨度的隐伏溶洞。由于溶洞与隧道掌子面之间的交互关系只存在这2种状态, 且溶洞与掌子面之间的位置关系主要影响盾构隧道与隐伏溶洞的安全距离的确定, 因此应当基于尖点突变理论依次从斜交、正交2种情况对安全距离进行分析。

2.1 溶洞与掌子面斜交情况下的安全距离分析

图3隧道掌子面与溶洞斜交图。岩溶区溶洞空间状态与盾构隧道掌子面斜交方位复杂性强, 在隧道附近的任意位置上都存在斜交于隧道的溶洞, 本文根据溶洞与掌子面间的不同距离, 与实际相结合选取最短距离后计算得出临界安全距离。

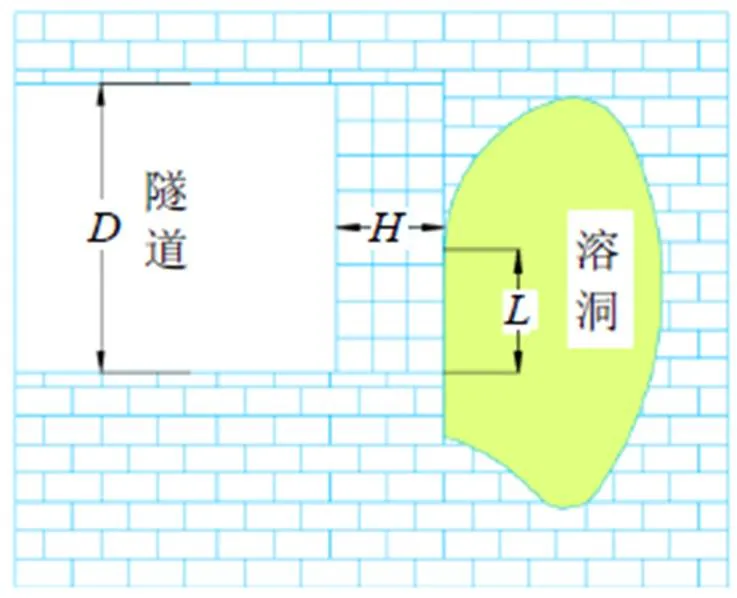
图3 隧道掌子面与溶洞斜交图

2.1.1 力学模型

本文通过尖点突变理论分析岩溶区盾构隧道溶洞与掌子面及岩墙组成的系统, 分析时需要将岩梁简化并提出下列假设: 不考虑水在长期作用下损坏岩腔的情况, 只考虑岩梁自重、填充物及周围环境中水压力的影响; 岩溶区盾构隧道具有完整的掌子面, 在垂直情况下对溶洞与隧道间的岩体简化后形成单位宽度、支座固定的岩梁, 同时岩梁上作用多种物质, 包括填充物、自重以及溶洞中的水压等; 通过对岩梁附近溶洞端地质构造应力进行简化后形成竖向推力, 在此基础上深入分析, 图4为其示意图。其中为溶洞对简化岩体的竖向推力,为隧道内部对简化岩体的竖向推力。

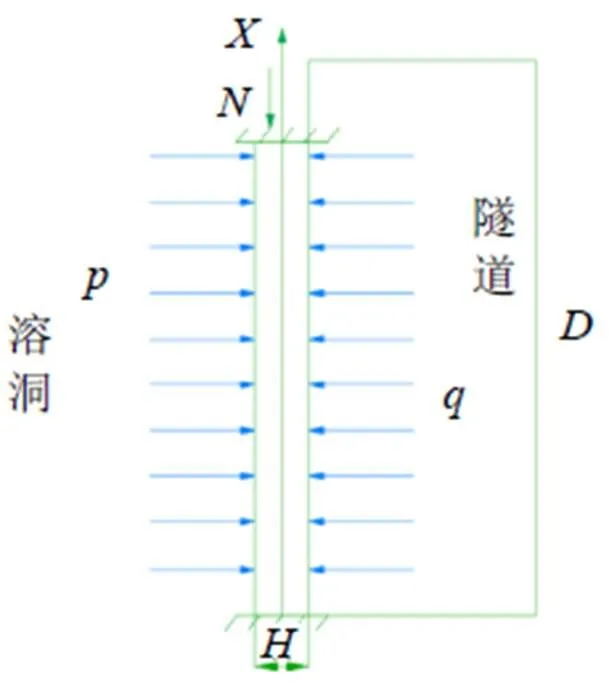
图4 力学模型简化示意图

2.1.2 势函数的建立

在此分析以上经过简化的假定力学模型, 然后对体系中的总势能进行计算, 基于此构建函数表达式, 以数学方式变换表达式成为尖点突变模型势函数, 岩墙梁轴线挠曲线公式为() =(1-cos(2π/)), 其中:为弧长(沿岩墙梁纵轴线的坐标轴的值);为岩墙梁轴线中点挠度;为岩墙梁的长度。

腔中填充物作用于岩墙梁上后生成系统势能、弯曲应变能, 同时外力在梁体上作用后所需的功能全部为岩墙梁系总势能, 则势函数

() =1+2–1–2, (2)

式中,1为岩梁的弯曲应变;2为系统增加的势能;1为垂直构造应力和重力所做的功;2为掌子面空气压力与岩溶水压力的做功之和, 由于空气压力通常影响较小, 故一般不予考虑, 即2有时也可仅指代岩溶水压力做功。采用弹性力学原理经过分析即可得出岩墙梁弯曲应变能系统势能的水平压力做的全部功、增加的所有量以及重力与垂直构造应力做的功, 由下列公式表示。

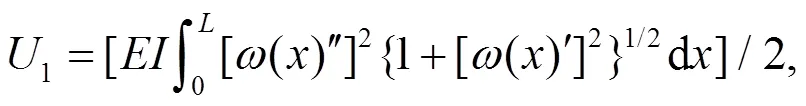
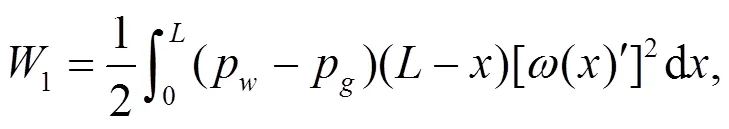
式中,为岩墙梁的弹性模量;p为岩溶区盾构隧道掌子面上的空气压力;为岩墙梁的惯性矩;p为岩溶水压力;为重力;为岩体的地质构造应力。

在式(2)中代入式(3)、(4)、(5)、(6)即可得出势函数的标准表达式

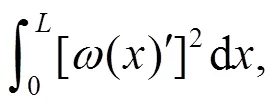
= 0时得到的泰勒级数将式(7)展开即可获得岩梁系统势函数, 对其简化得势函数标准表达式

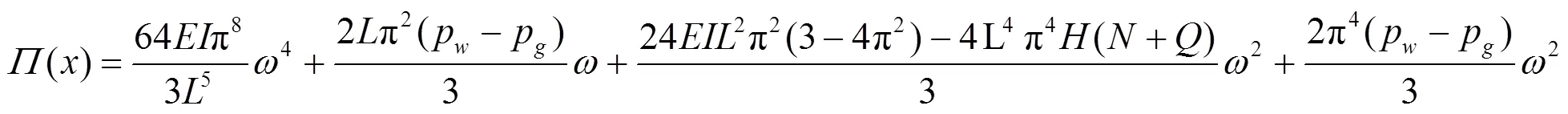
替换式(8)中的变量, 代换变量公式为

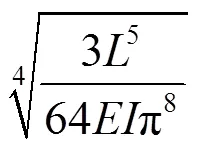
2.1.3 斜交时安全距离的确定

由分叉集方程在几何上的物理意义可知:、控制变量组成一个平面, 本平面内包含岩墙梁系统的所有奇数点, 在值小于等于0的情况下具有逾越分叉集, 由此可确定岩墙体突变的产生条件是≤ 0。、控制变量符合△ = 83+ 272= 0关系的条件下系统呈现临界平衡状态。故岩墙的临界破坏条件为

83+ 272= 0,≤ 0。 (10)

推导式(9)、(10)可得岩梁系统突变失稳的充要条件

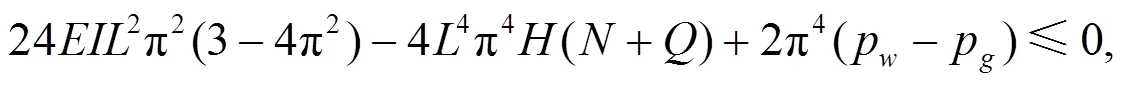
岩墙梁截面会对惯性矩值产生影响, 并假设岩墙梁宽度为单位宽度时获得惯性矩

=3/12, (12)

将式(12)代入作为突变失稳充要条件的式(11)中可得值, 该值为一个未知数, 在临界条件下计算岩梁系统

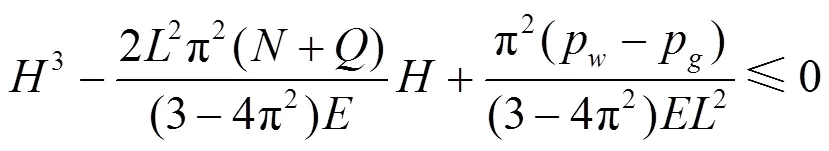
则临界安全距离

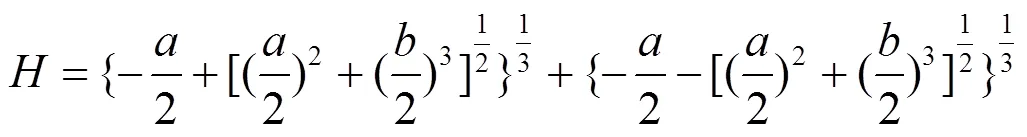
式中,

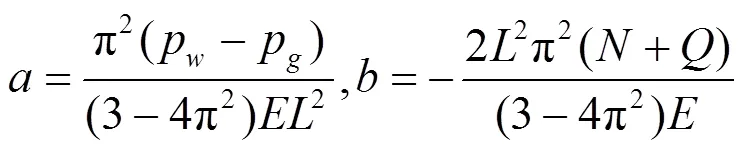
2.2 位于掌子面区域内的溶洞与掌子面正交情况下的安全距离分析

岩溶区盾构隧道掌子面与溶洞处于正交空间桩体下, 溶洞处于掌子面上, 在此可以视作隐伏溶洞是一个中小跨度的溶洞, 实际施工时溶洞曲线为垂直状态, 图5表示隧道掌子面与溶洞的正交状态, 表明了溶洞与掌子面之间的位置关系。

2.2.1 力学模型

采用尖点突变理论简化岩梁并提出下列假设: 岩溶区中具有完整的盾构隧道掌子面同时处于竖直状态, 在此需要简化溶洞与隧道间的岩体在单位宽度、支座固定的弹性梁的条件下对其深入分析; 对岩梁两端地质构造应力简化后为竖直方向上的推力, 进一步分析; 假设隧道底板与隧道间的距离由表示, 且≥0, 图6表示正交状态下的隧道与溶洞间的力学模型。

图5 隧道掌子面与溶洞正交图

2.2.2 确定正交时(溶洞位于掌子面区域内)的安全距离

根据以上分析得出标准势函数公式

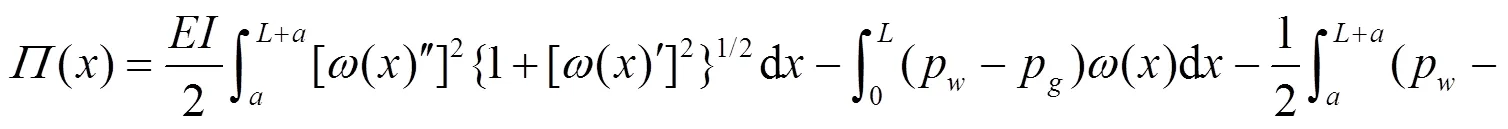
用= 0对应的泰勒级数对式(16)展开, 并取得岩梁系统势函数, 经过推导得岩梁系统突变失稳充要条件

2π44(0-p)(3-123-62)-44π4(+ 2)(2+ 3+ 32) +

82π4(32-2π2-12π23-12π2)≤ 0, (17)

基于单位宽度条件下, 采用同一种方式对岩梁墙惯性矩计算即可获得岩梁系统临界安全距离公式

图6 正交力学模型图

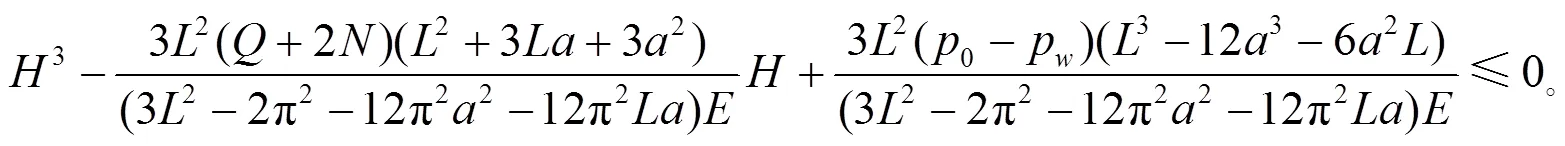
经过计算后获得临界安全距离

2.3 跨度大于隧道跨度的溶洞与掌子面正交情况下的安全距离分析

本文分析的课题是大跨度溶洞与岩溶区盾构隧道间的正交安全距离, 其本质是溶洞与隧道之间表现的失稳现象, 通过对溶洞跨度沿隧道轴线长度关系简化, 运用力学模型对其分析得到的效果如图7所示。

2.3.1 力学模型

(1)岩溶区溶洞附近与盾构隧道掌子面前方岩墙断面构成的平面为隧道轴线平面;

(2)施工过程中溶洞要将所有隧道断面跨过, 本模型应用的前提是选取固定支架的弹性圆板为岩梁。、分别表示为半径与板厚度, 均布压力由2部分构成, 分别为掌子面空气压力p与作用于掌子面前方岩墙上的岩溶水压力p。

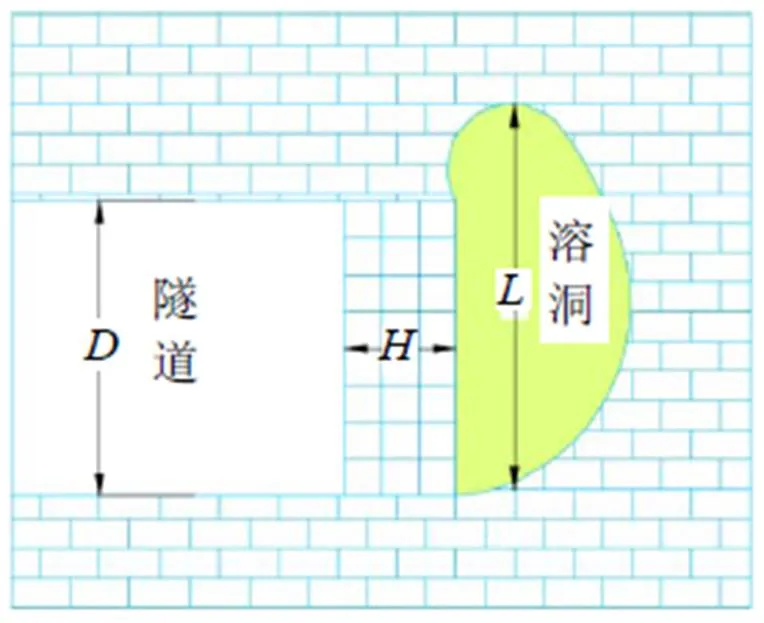
图7 隧道掌子面与溶与正交图

2.3.2 确定正交时(溶洞跨度大于隧道跨度)的安全距离

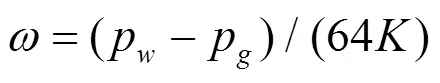
根据图8及弹性力学原理分析, 并假设本模型边界条件为[13]

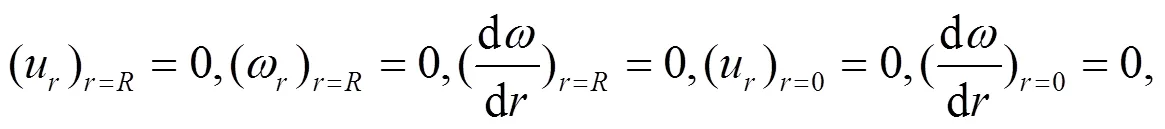
式中,u为径向位移。

由式(20)可知, 上述边界条件为不同级数, 选取其中第1项与第2项, 再按照弹性力学原理对其分析, 经过简化后获得边界条件公式[13]

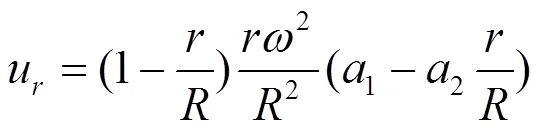
经过以上分析得到尖点突变理论势函数公式

, (22)

图8 正交力学模型图

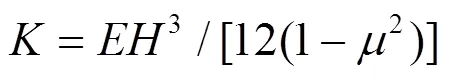
对式(22)推导后获得岩墙板临界厚度表达式

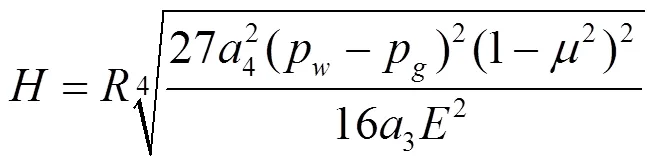
3 影响临界安全距离的因素分析

隐伏溶洞与开挖岩溶区盾构隧道具有多种空间状态, 对其力学模型简化后也表现出一定差别, 本文重点分析隐伏溶洞在2种空间状态下所需的安全距离, 所得结果概述如下:

(1) 隐伏溶洞与开挖岩溶区盾构隧道为正交状态(正交指的是隧道直径不高于溶洞跨度), 此时岩石泊松比、掌子面空气压力、隧道直径、岩溶水压等为主要因素。围岩弹性模量与临界安全距离间成反比, 增加围岩弹性模量后安全距离缩小, 也就是围岩等级与质量越高, 出现突水问题越少; 而增加隧道半径后临界安全距离也相应增加, 一次开挖面积越大出现突水现象越严重, 该现象符合实际施工状态;

(2) 假如溶腔空间状态与开挖岩溶区盾构隧道间斜交, 而此处影响安全距离的因素包括溶腔内水压力、弹性模量以及空气压力等。基于空间状态作为一项重要前提条件, 在该状态下分析计算临界安全距离的各项因素, 其中主要包括溶洞长轴线与隧道轴线间的夹角, 通过增加夹角而安全距离缩小, 增加围岩级别相应的安全距离增大;

(3) 假如溶腔空间状态与开挖岩溶区盾构隧道间为正交关系, 该状态下梁两端都需要承受地质应力产生的作用, 隧道深度增加后安全距离表现出非线性增长状态, 安全距离更长。

因此, 溶洞跨度不断增加的情况下安全距离也随之增加。由地下洞室围岩应力分布规律分析, 溶洞跨度对应力集中程度不会产生变化, 然而某种程度上对应力集中区间造成影响。

4 工程案例分析

深圳地铁14号线大运—宝荷工程区段隧道工程采用盾构法施工, 区间右线全长5 777.262 m; 左线全长5 573.421 m, 岩溶发育强烈, 大宝区间平均线岩溶率为31.6%, 可溶岩段总长约2 224.94 m。隧道洞身穿越地层主要为: ①微风化灰岩(1 677.2 m); ②微风化砂岩(90.9 m); ③中风化砂岩(53.6 m); ④强风化砂岩(411.5 m); ⑤全风化砂岩(293.9 m); ⑥强上软下硬地层(171.2 m); ⑦粉质黏土(66.9 m); ⑧强风化凝灰质石英岩(815.73 m); ⑨强上软下硬地层(84 m)。一般情况下隧道涌水量为每天6 150 m³, 隧道在雨洪期用水量最高为每天17 690 m³。在可溶岩段隧道施工时遇到溶隙与溶洞候出现突泥、突水等现象更严重。

位于D1K842+736~D1K842+765里程位置出现一个面积大的溶腔, 从掌子面右侧与左侧2个位置将钻杆打入后, 钻孔与钻杆之间的间隙会渗出部分水、泥等, 拔出钻杆喷出一定量的泥浆, 通常喷射泥浆的最长距离为12 m左右。按照探测结果显示, 掌子面前方最下面位置为溶腔, 积累的水较多, 同时夹杂大量泥沙, 溶腔深度达到22 m左右, 同时底板原涌泥位置涌出部分水, 测量其电压范围在0.36～0.40 MPa之间。图9表示隧道与溶洞的具体尺寸与位置关系。

通过查阅现场资料得出表1中所列相关参数, 掌子面与溶洞斜交时在固支梁模型中代入以上参数, 经过推导后获得式(16)、(17), 采用式(16)、(17)计算可得岩溶区隐伏溶洞与盾构隧道之间的临界安全距离值为5.73 m。

由图9可知, 岩溶区隐伏溶洞与盾构隧道之间的安全距离处于5～6 m区间内, 与计算的安全距离相比较小, 实际施工阶段要对其加固。通常盾构施工轮廓线以外5 m为加固注浆区间, 足以证明推导得到的隐伏溶洞与盾构隧道在斜交时, 再对单位宽度、两端支座固定的弹性梁模型安全距离简化取得的显著的效果, 为类似隧道工程的建设提供了指导。

图9 隧道与溶洞之间的溶洞尺寸及位置关系图(斜交)

表1 隧道临界安全距离参数表

位于D1K842+785~D1K842+815里程位置出现一个面积较广的溶腔, 在本里程段施工阶段, 周围以非均匀方式分布3～4个溶洞, 溶洞洞口直径最高为10～15 m左右, 距离洞口30～40 m位置处更宽广, 生成部分溶洞其深度大约为30 m左右, 出现突水问题, 具体尺寸及与隧道的位置如图10所示。

根据现场相关资料分析即可确定该类型盾构隧道与大跨度溶洞之间的安全距离, 其弹性模量的值为1 GPa, 岩溶水压力为0.5 MPa、泊松比为0.3; 2个不同变分参数相比取得的值为0.032 9,为盾构直径, 通常为12 m, 在式(23)中代入全部参数就可以计算获得隐伏溶洞与盾构隧道间的临界安全距离为6.25 m。

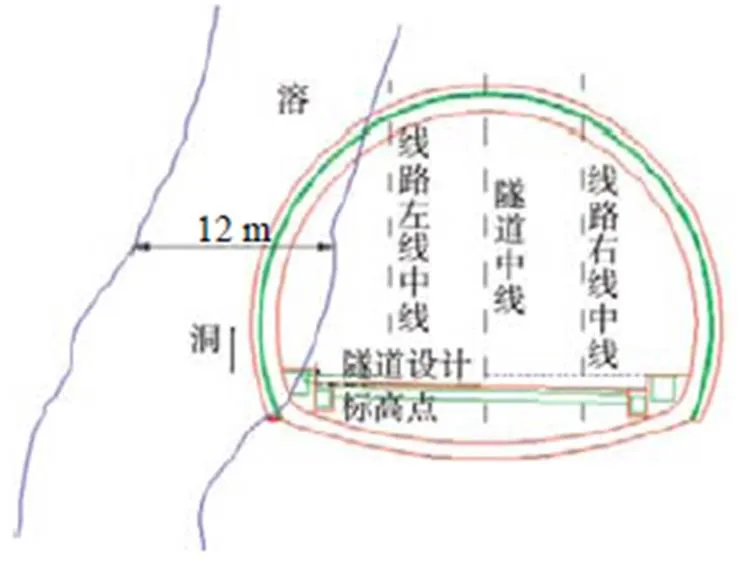
图10 隧道与溶洞间位置及溶洞尺寸图(正交)

由图10可知, 岩溶区隐伏溶洞与盾构隧道间距离接近6 m, 因此在施工阶段需要加固处理。常见的加固方式为预注浆, 应用预注浆方式可实现隐伏溶洞的加固。同时根据上述计算结果与6 m较接近, 因此可验证弹性圆板模型安全距离简化公式(式(23))在计算支座固定且隐伏溶洞与盾构隧道正交状态下溶洞安全距离的有效性更高, 可将其作为相似工程建设中的重要参考和理论依据。

5 结论

本文对岩溶区盾构隧道掌子面前方处于各种空间状态进行了综合分析, 基于弹性力学理论采用突变理论方法, 研究了掌子面与溶洞正交、斜交2种不同空间状态的临界安全距离, 得出如下结论:

(1) 分析隧道与溶洞间为正交、斜交, 选取单位宽度与固定支座的弹性梁作为力学模型研究;

(2) 通过建立可计算临界安全距离的非线性—尖点突变理论模型来分析隐伏溶洞与隧道处于正交状态时的力学模型, 推导得到临界安全距离的计算公式(14), 可用它来计算岩梁墙突变失稳时隐伏溶洞的临界安全距离;

(3)结合正在修建的深圳地铁14号线大运—宝荷工程区段盾构隧道工程的实例, 证明了采用突变理论获得处于各种状态下隧道和溶洞间的安全距离与实际施工相比具有显著一致性, 作为处置溶洞与岩溶区盾构隧道实际施工阶段的理论参考, 具有重要价值与应用意义。

[1] 郭佳奇, 乔春生. 岩溶隧道掌子面突水机制及岩墙安全厚度研究[J]. 铁道学报, 2012, 34(3): 105–111.

[2] 高峰, 周科平, 胡建华, 等. 充填体下矿体开采安全顶板厚度数学预测模型[J]. 岩土力学, 2008, 29(1): 177–181.

[3] 王勇, 乔春生, 孙彩红, 等. 基于SVM的溶洞顶板安全厚度智能预测模型[J]. 岩土力学, 2006, 27 (6): 1 000–1 004.

[4] 林杭, 曹平, 李江腾, 等. 采空区临界安全顶板预测的厚度折减法[J]. 煤炭学报, 2009, 34 (1): 53–57.

[5] 宋站平, 李宁, 邓良胜. 岩溶隧道岩层垮塌机理及隧道底板最小厚度分析[C] // 中国力学学会, 清华大学. 第15届全国结构工程学术会议论文集(第II册), 2006: 385–389.

[6] 刘超群, 彭红君. 隧道掌子面与溶洞安全距离分析[J]. 现代隧道技术, 2012, 49 (3): 109–113.

[7] 张梅, 张民庆. 岩溶隧道高压富水充填溶腔释能降压新技术[M]. 北京: 科学出版社, 2010.

[8] 赖永标. 隐伏溶洞与隧道间安全距离及其智能预测模型研究[D]. 北京: 北京交通大学, 2012.

[9] 付成华, 陈胜宏. 基于突变理论的地下工程洞室围岩失稳判据研究[J]. 岩土力学, 2008, 29 (1): 167–172.

[10] EC ZEEMAN. Bifurcation, Catastrophe, and Turbulence[J]. New Directions in Applied Mathematics, 1982: 109–153.

[11] 赵延林, 吴启红, 王卫军, 等. 基于突变理论的采空区重叠顶板稳定性强度折减法及应用[J]. 岩石力学与工程学报, 2010, 29(7): 1 424–1 434.

[12] 潘岳, 王志强, 等. 突变理论在岩体系统动力失稳中的应用[M]. 北京: 科学出版社, 2008.

[13] 姜德义, 任松, 刘新荣, 等. 岩盐溶腔顶板稳定性突变理论分析[J]. 岩土力学, 2005, 26 (7): 1 099–1 103.

Study on safety distance between shield tunnel and hidden karst cave

Zhao Yong

(China Railway South Investment Group Co Ltd, Shenzhen 518000, China)

To solve the problem of determining the safe distance between the shield tunnel and the hidden karst cave in shield construction, this paper studies the safety distance between the shield tunnel and the hidden karst cave based on the theory of elasticity, and establishes a nonlinear cusp catastrophe model for the calculation or prediction of the safety distance between the hidden karst cave and the tunnel face during the shield construction. The influence of various spatial states and shield tunnel face on safety distance is studied and analyzed in combination with shield tunnel project in karst area of Dayun-Baohe project section of Shenzhen metro line 14. The results show that: in the calculation of the safe distance between various space states and the hidden karst cave under the shield tunnel, the results are obtained by cusp catastrophe model are more accurate, which can be better applied to practice and effectively guide the construction of tunnel engineering.

shield tunnel; hidden karst cave; safe distance; catastrophe theory; karst area

U 458

A

1672–6146(2020)04––0080–07

10.3969/j.issn.1672–6146.2020.04.016

赵勇, 1094975625@qq.com。

2020–02–11

中国中铁股份有限公司科技研究开发计划(2019-重点-20-01)。

(责任编校: 张红)