通电螺线管磁场的双重数值积分法和可视化

莫云飞, 周群益, 侯兆阳, 周丽丽

通电螺线管磁场的双重数值积分法和可视化

莫云飞1, 周群益2, 侯兆阳3, 周丽丽4

(1. 长沙学院 电子信息与电气工程学院, 湖南 长沙, 410022; 2. 广州理工学院, 广东 广州, 510540; 3. 长安大学 理学院 应用物理系, 陕西 西安, 710064; 4. 赣南医学院 信息工程学院, 江西 赣州, 341000)

通电螺线管可以当作环电流密绕而成的, 本文利用环电流的磁场公式推导了通电螺线管磁感应强度的积分式, 将公式无量纲化。利用MATLAB的多维矩阵形成多维被积函数, 用二重数值积分计算场强。利用MATLAB的曲面指令绘制出磁感应强度2个分量以及合场强和方向曲面, 利用MATLAB的流线指令画出管内外的磁感应线, 充分显示了通电螺线管场强的分布规律。

通电螺线管; 磁感应强度; 数值积分; 无量纲作图

通电螺线管的磁场是电磁场理论中的一个典型问题, 文献[1–3]只计算轴线上的磁感应强度, 继而得到无限长通电螺线管在轴线上的场强公式; 文献[4–9]讨论了无限长通电螺线管内部的场强。文献[10–13]推导了有限长通电螺线管内外的场强的积分公式, 其中有些论文还画出了曲线。通电螺线管的磁场没有精确的解析解, 文献[14]研究了数值解, 并画出曲线族。文献[15–16]用MATLAB和Mathema- tica计算和研究场强、绘制曲线和曲面, 这是2种很好的方法。

1 通电螺线管的磁场

本文建立直角坐标系中场强的双重积分公式, 将公式无量纲化, 通过双重数值积分的方法计算了管内外磁感应强度的大小, 并用曲面和磁感应线显示磁场的分布规律。

如图1所示, 设螺线管的半径为, 长度为2, 通有电流。在圆环取一电流元d, 螺线管各匝线圈都是螺线形的, 在密绕的情况下可以当作多匝圆形线圈紧密排列而成。设单位长度上的匝数为, 在长度处取一线元d, 线圈匝数为d=d, 电流强度

d=d=d。 (1)

圆环形电流元d到点的轴坐标之间的距离为–, 环上的点到场点的距离

这里,是坐标和以及方位角和长度的四元函数=(,,,)。根据环电流产生的场强的公式, 环电流元在空间产生的磁感应强度的2个分量的微元为[17–19]

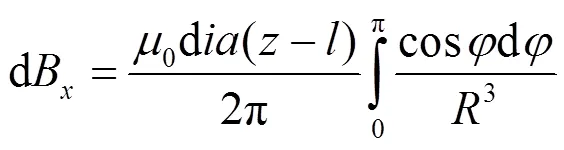
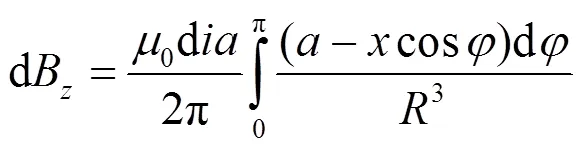
场强的2个分量

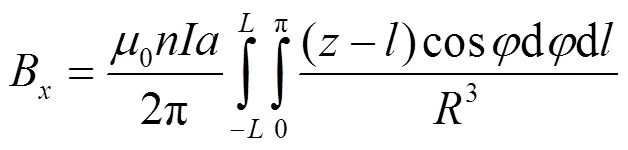
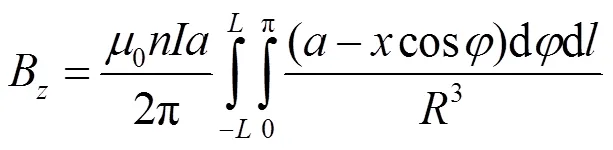
这是双重定积分公式,B=B(,)和B=B(,)是坐标和的二元函数。

合场强

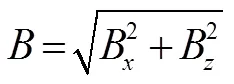
方向由角度确定

能量密度

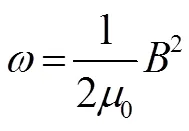
当= 0时, 距离

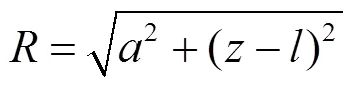
场强

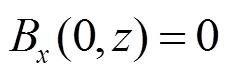
, (12)

这是轴线上的场强。

当= 0时, 距离

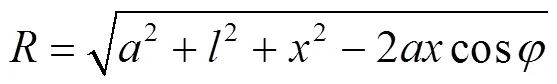
由于B(, 0)是的奇函数, 所以B(, 0) = 0,B(, 0)由式(6)决定, 这是中垂线上的场强。

2 磁感应强度公式的无量纲化

取半径为长度单位, 则无量纲的坐标

*=/,*=/。 (14)

无量纲的距离

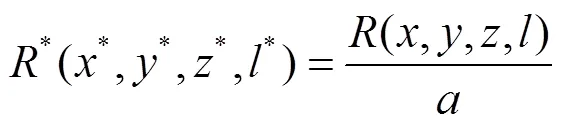
其中,*=/是无量纲的长度或相对长度。取0=0为磁感应强度单位, 则无量纲的磁感应强度的两个分量

, (16)

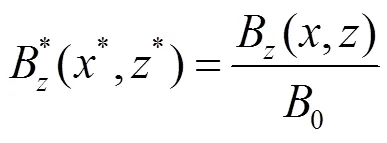
其中,*=/是无量纲的半长。

无量纲的合场强

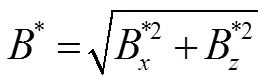
方向角

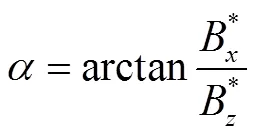
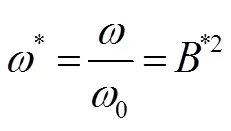
轴线上无量纲的场强

。 (21)

将磁感应强度公式无量纲化是为了便于数值计算。应用MATLAB, 将被积函数化为多维矩阵, 利用双重数值积分的方法求出平面内各点的磁感应强度。

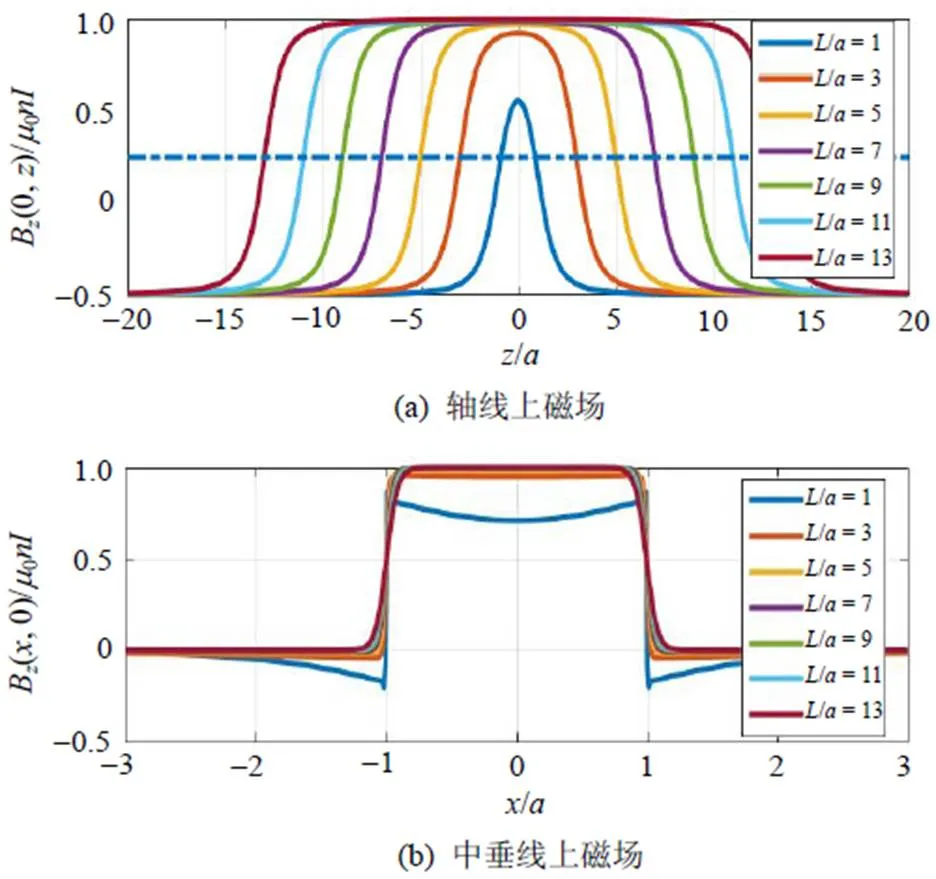
图2 通电螺线管轴线和中垂上的磁感应强度

3 磁场的可视化

根据磁感应强度的数值, 利用MATLAB的plot指令可以画出曲线族, 利用surf指令可以画出磁感应强度的曲面。利用流线指令streamline可以画出磁感应线。

(1) 通电螺线管轴线上的磁场如图2(a)所示。当管的长度一定时, 中间的磁感应强度最大; 当=时, 最大场强比较小。管越长, 管心处的磁感应强度就越接近于0, 轴线上均匀的范围就越大, 管口的场强约为最大场强的一半。通电螺线管中垂线上的磁场如图2(b)所示, 当=时, 中垂面内部的场强比较小, 管心处的场强最小; 管越长, 中垂面内部场强越均匀, 越接近于0, 外部场强越接近于0,= ±处两侧的场强变化越光滑。

(2) 当= 5时, 通电螺线管磁场的分量B的曲面如图3所示。管内外的B都很小; 只在在管口边缘,B有两对对称的“峰”和“谷”, “峰”和“谷”的B方向相反。轴线和中垂线上的场强B(, 0)和B(, π/2)为0, 其直线分布在水平面上。

(3) 磁场的分量B的曲面如图4所示。管内B形似一堵“墙”,= ±处是“墙”的边缘; 在管口,B迅速减小; 在管口的边缘,B< 0, 场强方向相反; 在管外, 除了管口附近,B很小。轴线和中垂线上的场强B(,0)和B(,π/2)曲线分布在曲面上。

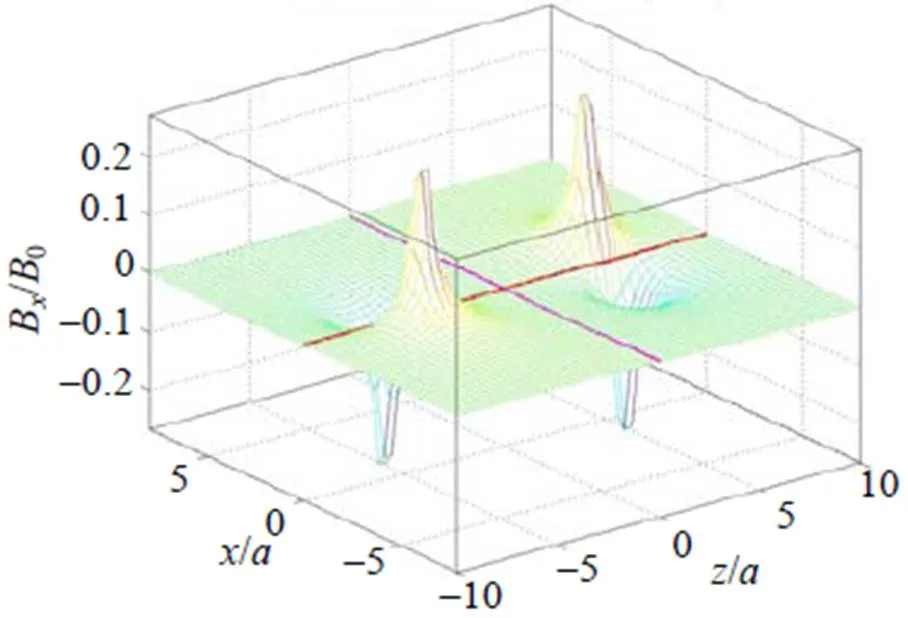
图3 通电螺线管磁场x分量的分布面(L = 5a)

(4) 合场强的曲面如图5所示。图5与图4类似, 不过,恒大于0; 除了管口边缘之外, 管外的曲面比较平, 也就是接近于0。轴线和中垂线上的场强(, 0) =B(, 0)和(, π/2) = |B(, π/2)|曲线分布在曲面上。场强的能量密度曲面与图5类似, 只是管外的曲面更加平, 也就是更加接近于0。

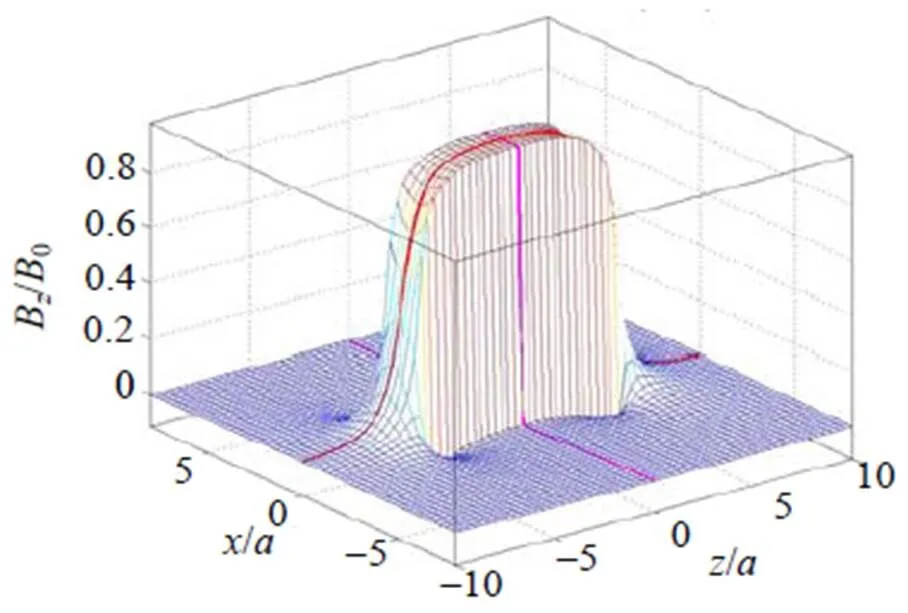
图4 通电螺线管磁场z分量的分布面(L = 5a)

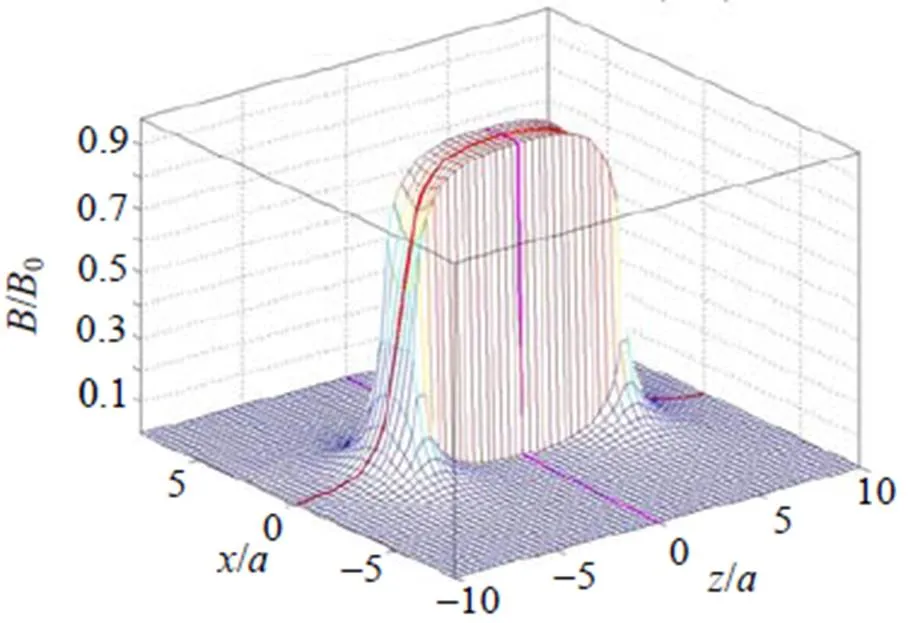
图5 通电螺线管合场强的分布面(L = 5a)

(5) 合场强的方向角曲面如图6所示。在= 0的轴线上,= 0。取轴为极轴, 在管内,几乎为0, 表示场强的方向几乎与轴线方向一致; 在管外,随极角的增加而增加,在= ± π/2处发生从-π到π的跃变。

(6) 通电螺线管内外的磁感应线如图7所示。在管内, 磁感应线密集而均匀, 可当作匀强磁场; 在管处, 磁感应线比较稀疏, 磁感应强度和能量密度都比较小。因此, 螺线管的能量可以当作均匀分布在管内处理。

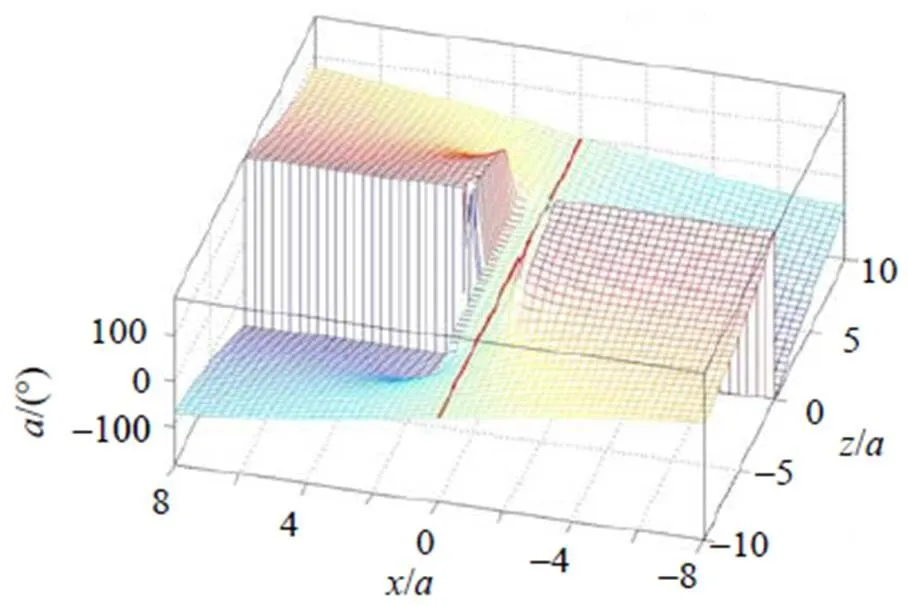
图6 通电螺线管磁场方向的分布面(L = 5a)

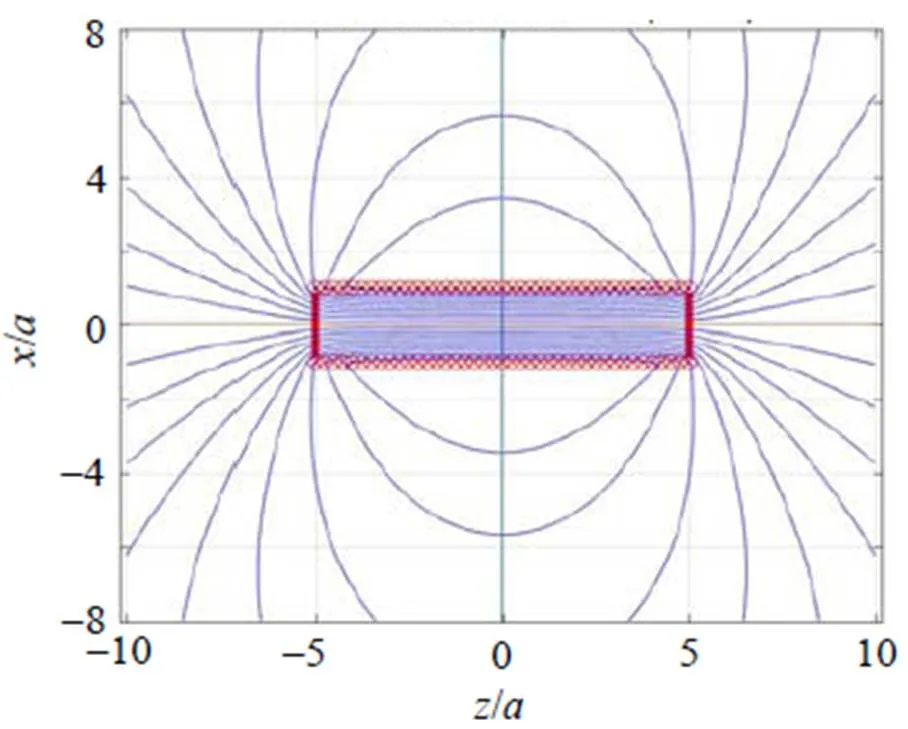
图7 通电螺线管的磁感应线(L = 5a)

4 结束语

本文解决了通电螺线管磁场的计算和可视化的问题: (1) 建立了直角坐标系中通电螺线管的磁感应强度的双重定积分公式; (2) 将公式无量纲化, 以便纯数值计算; (3) 用MATLAB做双重数值积分解决了计算问题; (4) 画出了彩色场强分布图和磁感应线图, 说明磁场的分布规律; (5)设计了2个MATLAB程序(见附录), 一个专门计算轴线和中垂线上的场强, 画出曲线族; 一个专门计算空间场强, 画出曲面和磁感应线。2个程序都不到100行。掌握程序设计方法是提出问题和解决问题的重要手段; (6) 程序采用双重积分公式。如果利用两类完全椭圆积分, 可以将双重积分公式化为单一积分公式, 计算效率更高, 曲面可以画得更加精致。

[1] 赵凯华, 陈熙谋. 电磁学[M]. 北京: 高等教育出版社, 2004.

[2] 张三慧. 大学物理学(下册)[M]. 3版. 北京: 清华大学出版社, 2010.

[3] 周群益. MATLAB可视化大学物理学[M]. 北京: 清华大学出版社, 2011.

[4] 成军. 无限长直均匀密绕载流螺线管的磁场[J]. 浙江师大学报(自然科学版), 2001, 24(4): 325–326.

[5] 王国强. 螺线管磁场的另一计算方法[J]. 高等函授学报(自然科学版), 2003, 16(2): 14–16.

[6] 张保军. 无限长载流螺线管磁场分布特点的证明[J]. 江苏技术师范学院学报, 2005, 11(6): 17–19.

[7] 丁红, 蓝海江. 无限长通电直螺线管内、外的磁感应强度[J]. 钦州学院学报, 2010, 25(3): 4–7.

[8] 牛中明, 于欣欣. 无限长直密绕通电螺线管磁场的一种简单计算方法[J]. 赤峰学院学报(自然科学版), 2018, 34(7): 11–12.

[9] 李永乐. 无限长密绕通电螺线管磁场简明计算[J]. 物理通报, 2017(11): 24–26.

[10] 程昌林, 王慧, 李业凤. 细导线密绕螺线管的磁场[J]. 物理与工程, 2003, 13(1): 6–8.

[11] 侯昭武. 通电线圈产生的电磁场强度[J]. 钦州学院学报, 2007, 22(6): 55–58.

[12] 李春生, 杨中海, 黄桃. 有限长通电螺线管空间磁场分析[J]. 现代电子技术, 2009, 32(11): 28–30.

[13] 梁丽萍. 关于载流长直螺线管磁场的讨论[J]. 教育教学论, 2014(18): 106–108.

[14] 刘耀康. 螺线管磁场的数值解[J]. 高师理科学刊, 2008, 28(1): 60–64.

[15] 惠小强, 陈文学. 有限长通电螺线管空间的磁场分[J]. 物理与工程, 2004, 14(2): 22–25.

[16] 王锴, 廖斌, 吴先映. 利用 Matlab研究多螺线管磁场分布[J]. 北京师范大学学报(自然科学版), 2013, 49(6): 565– 570.

[17] 向裕民. 圆环电流磁场的普遍分布[J]. 大学物理, 1999, 18(1): 14–17.

[18] 李海, 张玉颖. 圆环线电流的磁感应强度[J]. 大学物理, 1999, 18(6): 20–22.

[19] 朱平. 圆电流空间磁场分布[J]. 大学物理, 2005, 24(9): 13–17.

ringN1.m%通电螺线管轴线上和中垂线的场强分布(双重数值积分)

clear,l=1:2:13;%清除变量,半长度与半径比的向量

zm=20;z=-zm:0.1:zm;%横坐标的最大范围,自变量向量

[Z,L]=meshgrid(z,l);%坐标和比值矩阵

Bzr=((L-Z)./sqrt(1+(L-Z).^2)+(L+Z)./sqrt(1+(L+Z).^2))/2;%相对磁感应强度

fs=16;figure,subplot(2,1,1)%字体大小,创建图形窗口,选子图

plot(z,Bzr,'LineWidth',2)%画B的直角坐标曲线族

legend([repmat('itL/a m=',length(l),1),num2str(l')])%加图例

grid on,hold on,axis([-zm,zm,0,1])%加网格,曲线范围,保持图像

plot([-zm;zm],[0.5;0.5],'-.','LineWidth',2)%画水平零线

xlabel('itz/a','FontSize',fs)%显示横坐标

ylabel('itB_z m(0,itz m)/itmu m_0itnI','FontSize',fs)%显示纵坐标

title('通电螺线管轴线上的磁场','FontSize',fs)%显示标题

ph=linspace(0,pi);%角度向量

r='(1+l.^2+x.^2-2*x.*cos(ph)).^(3/2)';%距离三次方字符串

ddbzx=inline(['(1-x.*cos(ph))./',r],'x','l','ph');%x轴Bz分量被积内线函数

xm=3;x=linspace(-xm,xm,500);Bzx=[];%横坐标的最大范围,纵坐标向量,矩阵置空

for i=1:length(l)%按长度循环

li=linspace(-l(i),l(i));%管的长度向量(绕过奇点)

[X,L,PH]=ndgrid(x,li,ph);%设置数三维矩阵

dbzx=trapz(ddbzx(X,L,PH),3)/2/pi*ph(2);%x轴Bz分量对角度积分

bzx=trapz(dbzx,2)*(li(2)-li(1));%x轴Bz分量对长度积分

Bzx=[Bzx,bzx];%连接矩阵

end%结束循环

subplot(2,1,2)%选子图

plot(x,Bzx,'LineWidth',2)%画B的直角坐标曲线族

legend([repmat('itL/a m=',length(l),1),num2str(l')])%加图例

grid on%加网格

xlabel('itx/a','FontSize',fs)%显示横坐标

ylabel('itB_z m(itx m,0)/itmu m_0itnI','FontSize',fs)%显示纵坐标

title('通电螺线管中垂线上的磁场','FontSize',fs)%显示标题

ringN2.m

%通电螺线管的磁场(双重数值积分)

clear,lm=5;%清除变量,螺线管半长度与半径之比

r3='(1+(z-l).^2+x.^2-2*x.*cos(ph)).^(3/2)';%距离3次方字符串

ddBx=inline(['(z-l).*cos(ph)./',r3],'x','z','l','ph');%磁场x分量被积内线函数

ddBz=inline(['(1-x.*cos(ph))./',r3],'x','z','l','ph');%磁场z分量被积内线函数

ph=linspace(0,pi);%角度向量

l=linspace(-lm,lm);dl=l(2)-l(1);%管的长度向量(绕过奇点),管的长度间隔

zm=2*lm;z=linspace(0,zm,30);%z坐标范围,横坐标向量

xm=4/5*zm;x=linspace(0,xm,30);%x坐标范围,纵坐标向量

z(1)=sqrt(eps);x(1)=sqrt(eps);%零改为小量

[X,Z,L,PH]=ndgrid(x,z,l,ph);%设置四维矩阵

dBx=trapz(ddBx(X,Z,L,PH),4)/2/pi*ph(2);%Bx分量对角度积分

dBz=trapz(ddBz(X,Z,L,PH),4)/2/pi*ph(2);%Bz分量对角度积分

Bx=trapz(dBx,3)*dl;Bz=trapz(dBz,3)*dl;%Bx,Bz分量对长度积分

clear PH L%清除两个矩阵

sx=0.1:0.1:0.9;sz=0*sx+0.001;%磁感应线的起点坐标

figure,plot([0;0],[-xm;xm])%创建图形窗口,画竖直轴线

hold on,plot([-zm;zm],[0;0])%保持图像,画水平轴线

ms=6;z0=-lm:0.25:lm;%符号大小,管的横坐标向量

x0=ones(size(z0));%上管的纵坐标向量

plot(z0,x0,'ro',z0,x0,'r.','MarkerSize',ms)%画上面流出屏幕的电流

plot(z0,-x0,'ro',z0,-x0,'rx','MarkerSize',ms)%画下面流出屏幕的电流

plot([1 1]*lm,[-1+0.1;1-0.1],'r','LineWidth',3)%画右端的剖面

plot([-1 -1]*lm,[-1+0.1;1-0.1],'r','LineWidth',3)%画左端的剖面

grid on,axis equal,fs=16;%加网格,使坐标刻度相等,字体大小

title(['通电螺线管的磁感应线(itL m=',num2str(lm),'ita m)'],...

'FontSize',fs)%显示标题

xlabel('itz/a','FontSize',fs)%显示横坐标

ylabel('itx/a','FontSize',fs)%显示纵坐标

Z=Z(:,:,1);X=X(:,:,1);%取横坐标矩阵,取纵坐标矩阵

streamline(Z,X,Bz,Bx,sz,sx)%画第一象限磁感应线

streamline(-Z,X,-Bz,Bx,-sz,sx)%画第二象限磁感应线

streamline(Z,-X,Bz,-Bx,sz,-sx)%画第三象限磁感应线

streamline(-Z,-X,-Bz,-Bx,-sz,-sx)%画第四象限磁感应线

r3='(1+l.^2+x.^2-2*x.*cos(ph)).^(3/2)';%距离3次方字符串

ddbzx=inline(['(1-x.*cos(ph))./',r3],'x','l','ph');%x轴Bz被积内线函数

x=linspace(-xm,xm);%纵坐标向量

[XX,L,PH]=ndgrid(x,l,ph); %设置数三维矩阵

dbzx=trapz(ddbzx(XX,L,PH),3)/2/pi*ph(2);%x轴Bz分量对角度积分

bzx=trapz(dbzx,2)*dl;%x轴Bz分量对长度积分

Z=[-fliplr(Z),Z;-fliplr(Z),Z];%四象限横坐标矩阵

X=[flipud(X),flipud(X);-X,-X];%四象限纵坐标矩阵

Bz=[fliplr(flipud(Bz)),flipud(Bz);fliplr(Bz),Bz];%四象限Bz矩阵

Bx=[-fliplr(flipud(Bx)),flipud(Bx);fliplr(Bx),-Bx];%四象限Bx矩阵

B=sqrt(Bz.^2+Bx.^2);%总场强

A=atan2(Bx,Bz)*180/pi;%场强角度

BC={Bx,Bz,B,A,B.^2};%数据元胞

zc={'itB_x/B m_0','itB_z/B m_0',...

'itB/B m_0','italpha m/circ','itomega/omega m_0'};%竖坐标元胞

tc={'itx m分量','itz m分量','合场强itB m','方向',... '能量密度itomega m'};%标题的一部分

z=linspace(-zm,zm);%横坐标向量

bzr=((z+lm)./sqrt(1+(z+lm).^2)-(z-lm)./sqrt(1+(z-lm).^2))/2;%轴线上磁感应强度

for i=1:length(BC)%循环

figure,mesh(Z,X,BC{i})%创建图形窗口,画曲面

box on,axis tight%加框,帖轴

t=['通电螺线管磁场',tc{i},'的分布面(itL m=',...

num2str(lm),'ita m)'];%标题

title(t,'FontSize',fs)%显示标题

xlabel('itz/a','FontSize',fs)%显示横坐标

ylabel('itx/a','FontSize',fs)%显示纵坐标

zlabel(zc{i},'FontSize',fs),hold on%显示竖坐标,保持图像

if i==1,plot3(z,0*z,0*z,'r',0*x,x,0*x,'m','LineWidth',2),end%画线

if i==2,plot3(z,0*z,bzr,'r',0*x,x,bzx,'m','LineWidth',2),end%画线

if i==3,plot3(z,0*z,bzr,'r',0*x,x,abs(bzx),'m','LineWidth',2),end%画线

if i==4,plot3(z,0*z,0*z,'r','LineWidth',2),view(-75,60),end%调整视角

if i==5,plot3(z,0*z,bzr.^2,'r',0*x,x,bzx.^2,'m','LineWidth',2),end%画线

end%结束循环

Calculating the magnetic filed of current solenoid according to a double numerical integral and its visualization

Mo Yunfei1, Zhou Qunyi2, Hou Zhaoyang3, Zhou Lili4

(1. School of Electronic Information and Electrical Engineering, Changsha University, Changsha 410022, China; 2. Guangzhou Institute of Science and Technology, Guangzhou, 510540, China; 3. School of Science, Chang’an University, Xi’an 710064, China; 4. Department of Information Engineering, Gannan Medical University, Ganzhou 341000, China)

The current solenoid can be considered that it is composed of the tightly wound loop current, this work has been obtained the integration formula of the magnetic field for current solenoid depending on the magnetic field formula for ring current, and the formula is also nondimensionalized. After the multi­dimensional integrand has been produced by using the multi-dimensional matrix in MATLAB, then the magnetic field is obtained according to a double numerical integral. The two components of magnetic field, the composite of filed and the direction surface are drawn by using the surface instruction of MATLAB. The magnetic lines inside and outside of the solenoid are also drawn with the streamline instruction of MATLAB, which can fully show the distribution characterization of magnetic field strength in the current solenoid.

current solenoid; magnetic field;numerical integral; dimensionless drawing

O 441

A

1672–6146(2020)04–0020–07

10.3969/j.issn.1672–6146.2020.04.004

周群益,1845901757@qq.com。

2020–04–24

湖南省自科基金(2018JJ3560); 长沙市科技计划项目(kc1809022); 湖南省教育厅科学研究项目(19C0176)。

(责任编校: 刘刚毅)