基于F-AHP评价法的PPP项目风险评价研究

李云

基于F-AHP评价法的PPP项目风险评价研究

李云

(湖南城建职业技术学院 建筑设备工程系, 湖南 湘潭, 411101)

运用模糊层次评价法(F-AHP)对PPP项目进行风险评价, 对风险因素进行了分析, 建立了评价标准和决策准则。针对风险等级的决策目标, 构建了由5个一级风险因素和20个二级风险因素构成的评价指标体系, 通过专家问卷调查对项目二级风险进行了评估, 确定了发生的概率。运用模糊层次评价法对PPP项目案例的因素指标进行定性分析及定量计算, 得到了案例中一级风险因素评价指标的风险评价得分及风险大小排序, 得知该PPP项目的成本费用是主要的风险控制因素, 通过该项目总体风险评价计算可判断该项目整体风险为中等。因此, 模糊层次评价法是对PPP项目进行风险评价行之有效的方法, 可以为PPP项目的风险决策提供了依据。

模糊层次评价法; 层次分析法; PPP模式; 风险因素; 风险评价

PPP项目投资模式[1–2](Public-Private-Partnerships, 简称PPP)是政府借助社会资本共同合作来完成公共基础设施项目投资, 它是公共基础设施投资建设的创新模式[3]。由于基础设施项目参与方多、投资大、周期长、风险多、难控制等特点, 因此需要对该类型项目进行科学的风险识别和风险评估研究。研究PPP模式下基础设施项目的风险管理, 必须建立风险管理概率模型和风险评价模型, 然后进行定性与定量的分析, 才有助于基础设施的PPP项目风险管理的系统化研究[4]。

1 F-AHP评价法的构建

1.1 AHP层次分析法

美国Thomas L. Saaty在20世纪70年代开发Analytic Hierarchy Process, 称之为AHP层次分析法, 它是一种基于数学和心理学的组织和分析复杂决策的结构化技术[5]。决策目标构建是层次分析法首先要明确的问题, 并对目标的影响因素进行量化处理, 使各因素与目标按照一定的规则统一在一个合理的评价体系内, 帮助决策者做出科学的判断[6]。通常情况下AHP层次分析法由3步构成。第1步构建结构层级模型。按照某种属性把各个因素分解成若干层级, 最上层级为目标层, 中间层级为准则层或指标层, 最后层级为方案或对象层。第2步构造对比矩阵。结构层级模型的第2层起, 用对比较法和1-9标度法比较重要度构造对比矩阵, 对最大特征根和相对应特征向量进行一致性检验。第3步构造判断矩阵。用两两重要度之比来表示出2个方案的相应重要性程度的等级, 并按其重要性程度评定等级。

1.2 模糊数学评价法

模糊数学法的数学模型的基础是确定模糊子集与隶属函数, 设是论域, 称映射。假设():®[0, 1]确定了集合上的某一模糊子集, 其映射()称作的隶属函数, 就称对的隶属程度。映射()取0或1时,()就是特征函数, 模糊子集对应的就是经典子集。令() = 0.5时, 点称为的过渡点, 其最具模糊性[7]。确定隶属函数的步骤如下:

(1) 建立各个指标因素集

= {1,2,3,…,e}。 (1)

(2) 构建评价集= {1,2,3,…,S}, 建立单因素评判, 即建立一个从到()的模糊映射。

=®()。 (2)

由可以导出模糊关系

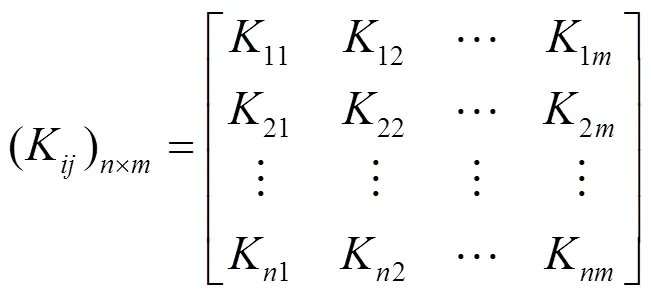
其中K=第级评价登记的人数/全部测评人数, 为第个影响因素对应第评判的隶属度。

(3) 计算权重。每一个因素对目标的影响程度是存在差异性, 这种差异就需要对各因素设定一个权重w来衡量, 设为

= {1,2,3,…,w}。 (4)

(4) 建立综合评价体系。评价对象的模糊综合评价假定为表示, 则

=×, (5)

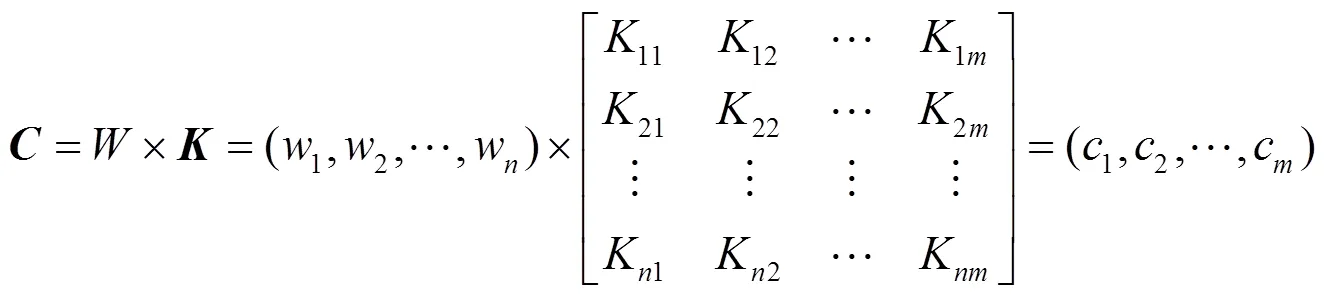
1.3 F-AHP评价法

把层次分析法的定性分析和模糊数学评价法的定量计算结合起来, 建立一种新的综合评价方法, 即F-AHP评价法, 它能够对风险不确定性项目进行合理的风险评价[8–9]。F-AHP评价法先将不确定性项目的风险因素用层次分析法进行了定性分析, 再将风险因素用综合模糊数学方法进行了定量化计算, 确保风险评估值的可靠性。具体评价过程是首先用模糊层次评价法计算权重, 再对影响因素进行分层分析、计算及评价, 然后进行综合判断。

2 模糊层次评价法权重计算

2.1 建立层级要素间比较判断矩阵

在构建的风险评价模型中, 比较同一指标层风险因素的重要性, 并对重要性程度进行排序, 再根据各因素重要程度来建立判断矩阵

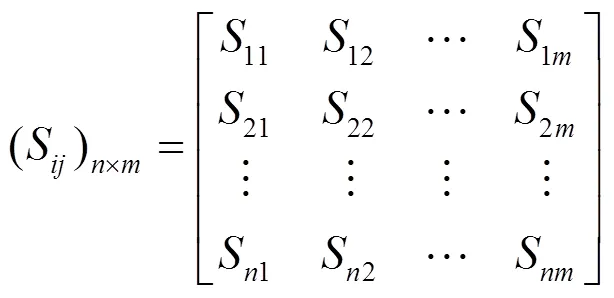
式中S隶属于目标层S, 表示准则层风险因素。在层次分析法中, 对评判矩阵的元素的重要程度需要进行量化处理, 以数字的形式形成量化矩阵。本文采用常用的1-9标度方法(见表1)。

表1 判断矩阵的相对重要性的标度值及比较规则

2.2 权重计算方法

用创建的F-AHP评价法对不确定性问题进行评价, 其权重向量值计算步骤如下:

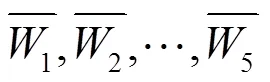
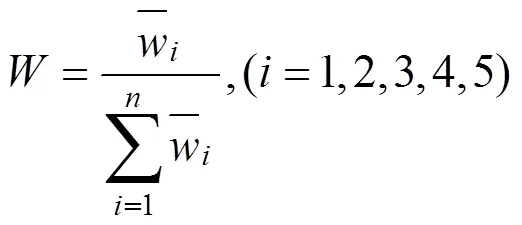
2.3 一致性检验

为了确保F-AHP评价法的适用性, 需要对判断矩阵进行一致性检验。依据一致性检验原则, 当满足CCR<0.1时, 说明判断矩阵满足一致性检验[10]。

3 影响因素评价

3.1 一级模糊综合评价

风险因素权重确定后, 就建立了一个评价等级集。评价等级集= {1,2,3,…,U}, 且U(= 1, 2, 3, …,)为可能评判结果。在不确定性因素量化分析过程中, 通常取值为模糊语言[0, 1]之间, 本文确定评价等级集

= {很小, 较小,中等, 较大, 很大} = {0.1, 0.3, 0.5, 0.7, 0.9}。 (10)

因此, 评价等级集的标准隶属度

= {0.1, 0.3, 0.5, 0.7, 0.9}。 (11)

这样就可以得到一级模糊综合评价矩阵(式(3))。

3.2 二级模糊综合评价

根据B=E×K, 通过评判准则层对各指标子集可以计算出各评价指标的等级。

3.3 三级模糊综合评价

依据=×, 在准则层之间进行三级模糊综合评判。通过=×T计算目标层的综合隶属度, 再对照评价集可以确定目标层的风险等级。

4 案例应用

4.1 项目概况

长沙市某高架桥是一条南北向城市快速路, 该项目采用PPP项目投资模式建设。设计北起福元路, 南至湘府路, 总长为16.6 km, 设计车速为80 km/h, 主线全线高架双向6车道, 采用连续梁桥和简支梁桥的桥型,

4.2 项目风险评价

4.2.1 构建风险因素评价指标集

1级风险因素评价指标集= {1,2,3,4,5} = {合作风险, 金融风险, 政策风险, 成本费用风险,自然条件风险}。2级风险因素评价指标集1= {11,12,13};2= {21,22,23,24};3= {31,32,33};4= {41,42,43,44,45,46,47};5= {51,52,53}。

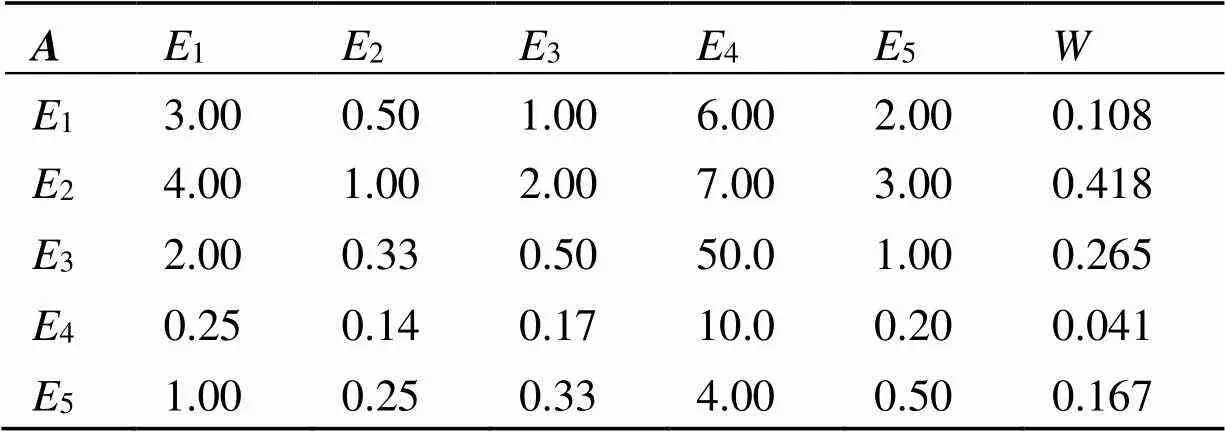
表2 判断矩阵(A)

4.2.2 建立对比判断矩阵

为了比较同一层风险因素之间的相互重要性, 通过多次问卷调查收集了8个一级评价指标和30个2级评价指标, 再聘请10名专家召开认证会进行评价体系指标的筛选, 确定了5个一级风险指标和20个二级风险指标, 然后10名专家独立对风险评价指标进行评分, 并取其平均值来计算各层级因素指标的权重, 构建了首层因素之间的判断矩阵(见表2)。表中即为首层风险指标的权重值, 由一致性检验公式计算出了判断矩阵的最大特征根max= 0.453,C= 0.113,C= 0.098 3 ≤ 0.1,满足一致性要求。同理, 建立二级指标层中风险因素之间的判断矩阵(见表3—表7)。

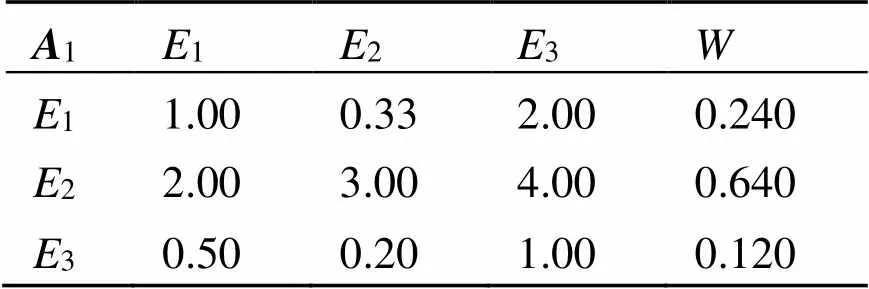
表3 合作风险指标判断矩阵(A1)

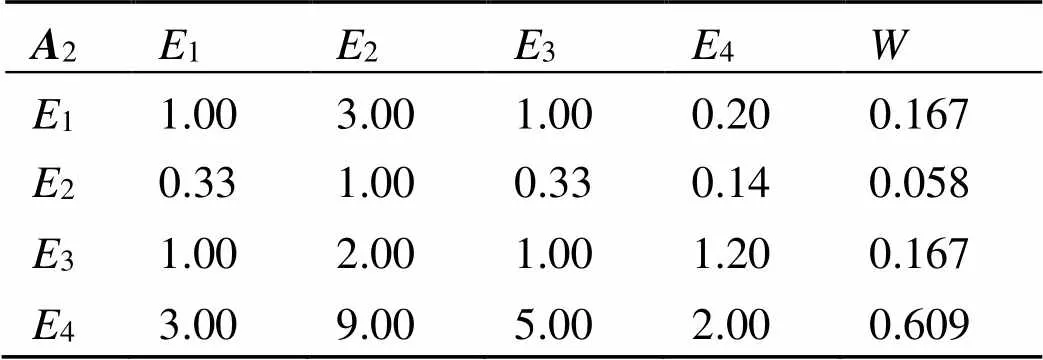
表4 金融风险指标判断矩阵(A2)

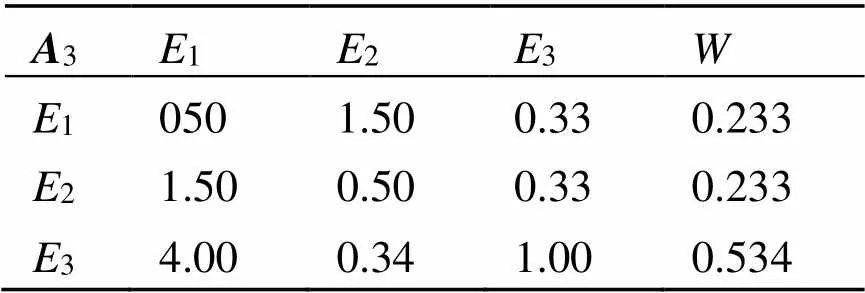
表5 政策风险指标判断矩阵(A3)

由表3可知, 此矩阵max= 0.108,C= 0.054,C= 0.098 2, 符合判断矩阵一致性要求。合作风险主要包括合作障碍、权责分配不当以及人事风险。

由表4可知, 此矩阵max= 0.274,C= 0.091 3,C= 0.1, 符合判断矩阵一致性要求。金融风险主要包括国际汇率、国家利率、通货膨胀以及社会融资环境。

由表5可知, 此矩阵max= 0.106,C= 0.053,C= 0.096 3, 符合判断矩阵一致性要求。政策风险主要是政府信用以及国家政策变动。

由表6可知, 此矩阵max= 0.813,C= 0.135 5,C= 0.096 9, 符合判断矩阵一致性要求。成本费用风险贯穿于项目建设和运营的全寿命周期。

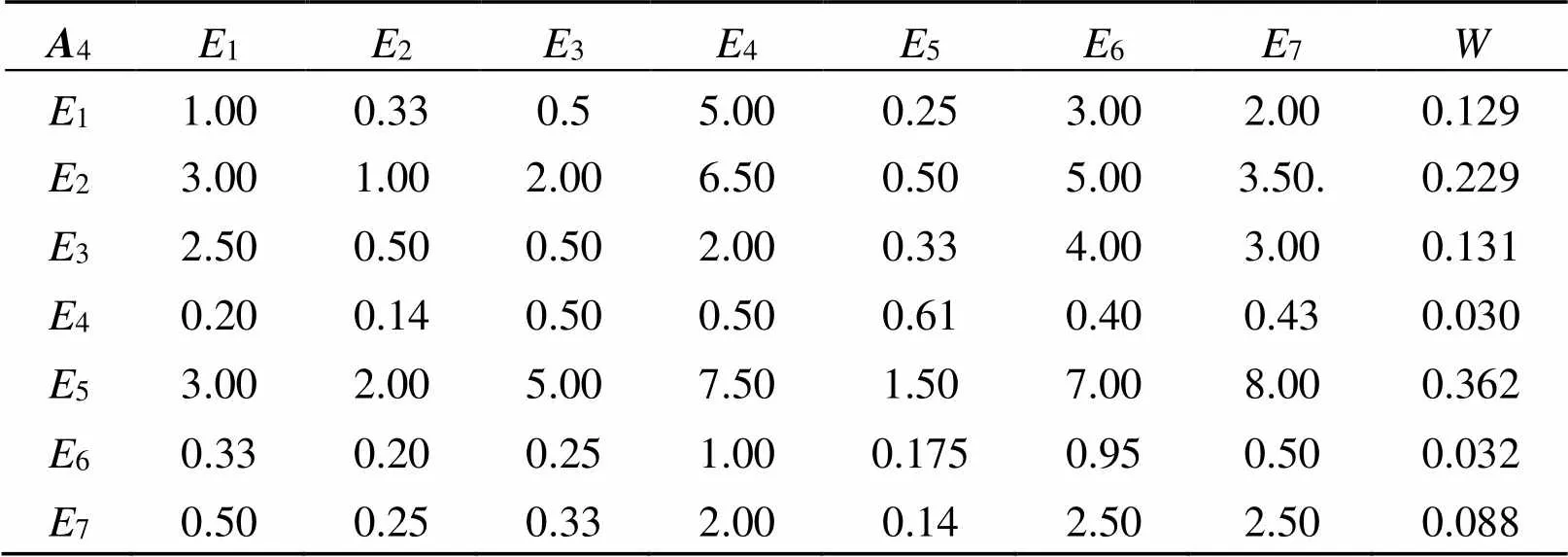
表6 成本费用风险指标判断矩阵(A4)

由表7可知, 此矩阵max= 0.107 3,C= 0.053 7,C= 0.097 3, 符合判断矩阵一致性要求。自然条件风险在项目建设过程中时刻存在, 气候条件变化、不可抗力发生、当地对环保的要求等等都影响项目的投资。

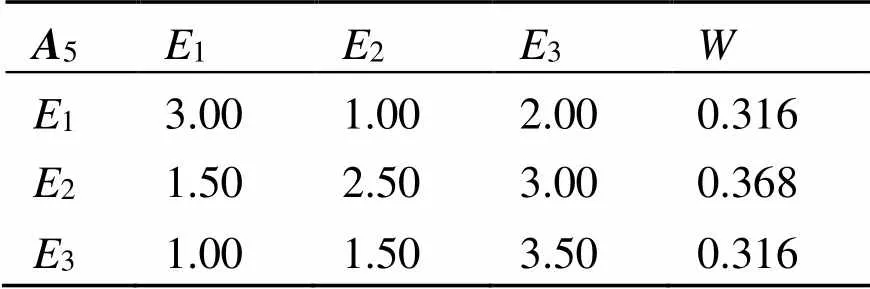
表7 自然条件风险指标判断矩阵(A5)

4.2.3 模糊综合评价

(1) 确立评价因素及评语集合。通过聘请的10位专家对项目评价指标体系的风险进行评估打分, 并进行整理确定风险因素发生的概率及评估值(见表8)。

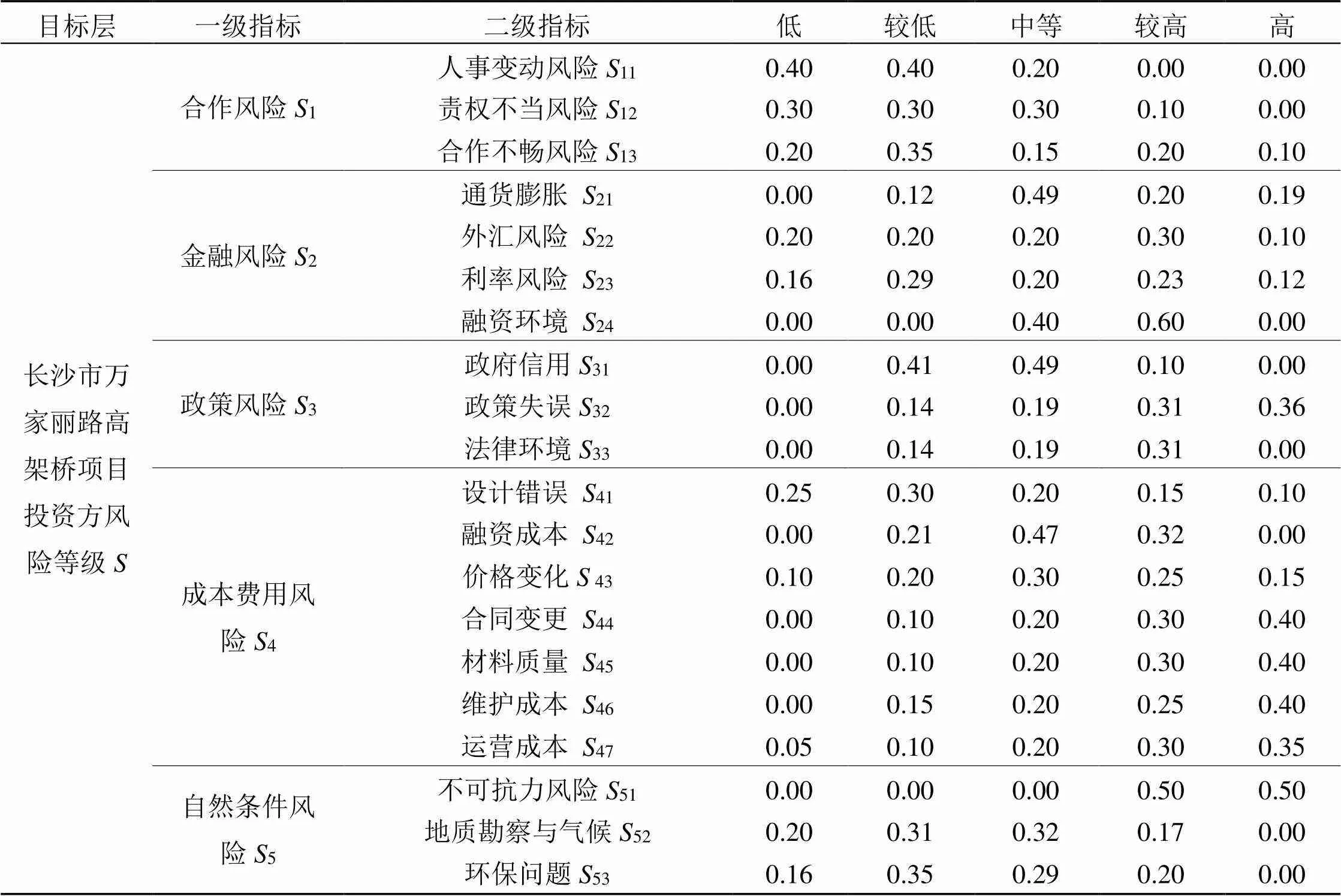
表8 风险评价体系及概率评估值表

(2) 确定评价隶属矩阵。依据表8可得

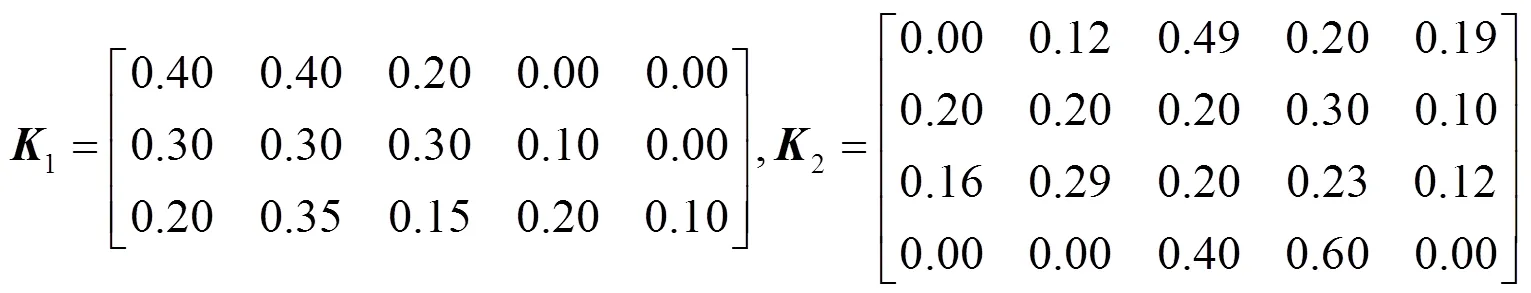
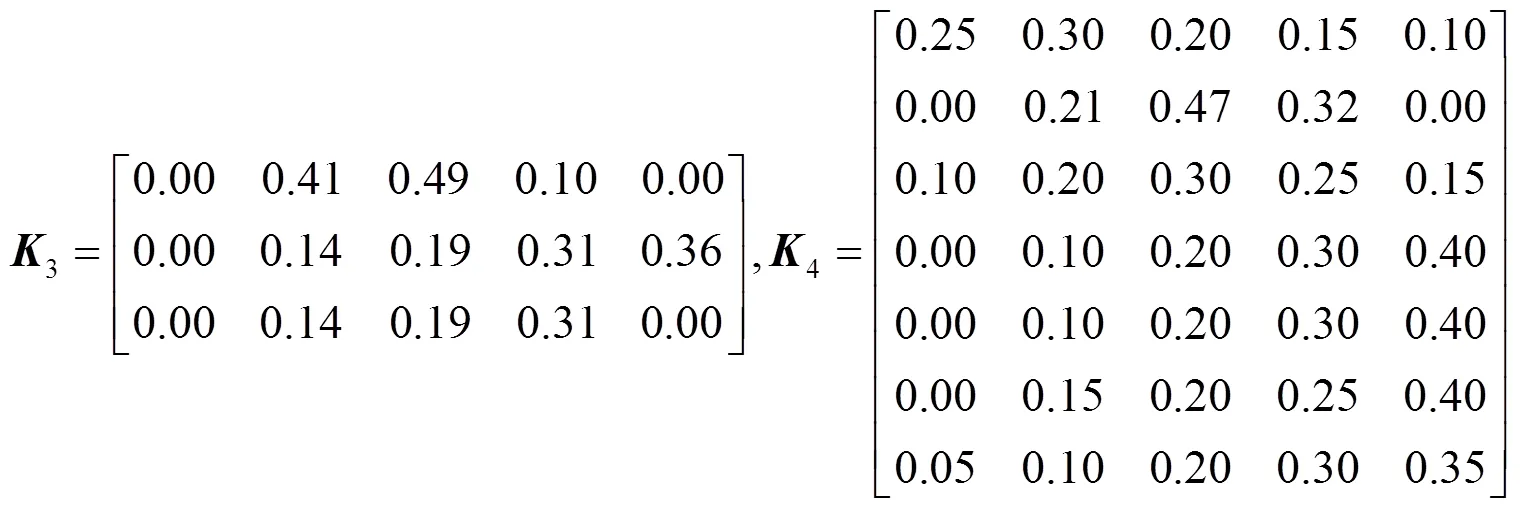
(3)各二级指标因素权重集。根据式(4), 由表3~表7可以得到各二级指标因素权重集如下:W1 = {0.240, 0.640, 0.120};W2 = {0.167, 0.058, 0.167, 0.609};W3 = {0.233, 0.233, 0.534};W4 = {0.129, 0.229, 0.131, 0.030, 0.369, 0.032, 0.088};W5 = {0.316, 0.368, 0.316}。分别对各风险因素进行综合评价并归一化处理如下:1=W1 ×1= (0.312, 0.331, 0.258, 0.088, 0.012);2=W2 ×2= (0.038, 0.080, 0.370, 0.455, 0.058);3=W3 ×3= (0.000, 0.203, 0.260, 0.084);4=W4 ×4= (0.050, 0.166, 0.277, 0.279, 0.236);5=W5 ×5= (0.124, 0.225, 0.209, 0.284, 0.158)。

(4) 确定三级模糊矩阵。计算综合模糊评价矩阵

4.3 结果分析

本文所有一级指标风险因素得分分别为: 合作风险为0.077, 金融风险为0.167, 政策风险为0.297, 成本费用风险为0.323, 自然条件风险为0.092, 因此成本费用风险最高。成本费用风险是该PPP项目的主要风险因素, 项目实施过程中要特别关注成本费用风险。由结果可知, 长沙市万家丽路高架桥项目最终总体风险评价分为0.515 8, 接近0.5, 可以判断该项目整体风险为中等。

5 结论

模糊层次评价法(F-AHP)能够有效地解决PPP项目风险评价过程中定性分析转化为定量计算, 并保证了其计算精度。因此, 它是PPP模式下基础设施项目投资方进行风险管理的一种风险评价方法。模糊层次评价法能应用于项目不同阶段的风险评价, 从而能保证PPP项目的动态风险评估结果的可靠性。

[1] 岳昱博.PPP模式下大型基础设施项目投资风险研究与对策[D]. 长沙: 中南林业科技大学, 2019: 32–49.

[2] 孙振正. PPP模式下基础设施项目融资风险管理研究[D].上海: 华东理工大学, 2010: 35–38.

[3] 张晨. PPP项目风险分担: 发达国家与发展中国家的比较分析[D]. 天津: 天津大学, 2013: 60–63.

[4] 欧宗奇. PPP模式下城市基础设施项目投资方风险评价研究[D]. 合肥: 安徽建筑大学, 2016: 43–47.

[5] C.B Chapman, Cooper D F. Risk analysis for large projects: Models, Methods and Cases [M]. John Wiley & Sons, 1987.

[6] Hastak M, Shaked A. ICRAM-1: Model for international construction risk assessment [J]. Journal of Management in Engineering, 2000, 16(1):59–69.

[7] PPIAF. The APMG Public-Private Partnership (PPP) Certification Guide [M]. Newyok: The World Bank Group, 2016: 74–80.

[8] Katrin Fischer, Katja Leidel, Alexander Riemann, et al. An integrated risk management system (IRMS) for PPP projects [J]. Jou-rnal of Financial Management of Property and Construction, 2010: 45–47.

[9] Xiao-Hua Jin, Guomin Zhang, Rebecca J. Yang.Factor analysis of partners'commitment to risk management in public- private partnership projects [J]. Construction Innovation: Information, Process, Management, 2012: 43–46.

[10] 魏庭明. XP公司采购管理优化策略研究[D]. 上海: 东华大学, 2019.

Research on PPP project risk evaluation based on F-AHP

Li Yun

(Hungn Urban Construction College, Department of Construction Equipment Engineering, Xiangtan 411101, China)

Fuzzy Analytic Hierarchy Process (F-AHP) is used to evaluate the risk of PPP project. Firstly, the risk factors are analyzed, and the evaluation criteria and decision-making criteria are established. Aiming at the decision target of risk grade, an evaluation index system consisting of 5 first-level risk factors and 20 second-level risk factors is constructed, and the second-level risk of the project is evaluated through expert questionnaire survey, and the probability of occurrence is determined.The qualitative analysis and quantitative calculation of the factor index of the PPP project case are carried out by using the fuzzy AHP evaluation method, and the risk evaluation score and risk ranking of the first-level risk factor evaluation index in the case are obtained. It is known that the cost of the PPP project is the main risk control factor, and the overall risk of the project can be judged to be medium through the overall risk evaluation calculation. Therefore, the fuzzy AHP evaluation method is an effective way to evaluate the risk of PPP projects, which can provide a basis for the risk decision-making of PPP projects.

fuzzy hierarchical evaluation process (F-AHP); analytic hierarchy process; PPP mode; risk factor; risk assessment

TU 9

A

1672–6146(2020)04–0069–06

10.3969/j.issn.1672–6146.2020.04.014

李云, liyunliuji@163.com;

2020–05–11

湖南省社科基金资助项目(18YBJ29); 湖南省教育科学“十三五”规划课题资助项目(XJK19CZY056); 湖南城建职业技术学院科学研究项目(19KTZD03)。

(责任编校: 刘刚毅)