不同施工条件下双线盾构隧道施工引发地表变形规律研究

牟天光, 祝江林

不同施工条件下双线盾构隧道施工引发地表变形规律研究

牟天光1, 2, 祝江林1, 2

(1. 湖南科技大学 岩土工程稳定控制与健康监测湖南省重点实验室, 湖南 湘潭, 411201; 2. 湖南科技大学土木工程学院, 湖南 湘潭, 411201)

为了了解双线盾构隧道在不同条件下施工引发地表变形规律, 依托南宁地铁3号线某盾构区间工程, 采用数值分析的方法, 结合现场实测数据, 分析了双线盾构隧道施工横向地表沉降规律, 结果表明: (1) 地表沉降表现出沉降槽形式, 最大地表沉降量出现在两隧道之间偏先行洞一侧; (2) 当土仓压力小于朗肯理论主动土压力时, 土仓压力增加20%, 地表沉降量减小约10%; (3) 随着隧道埋深的增加, 地表沉降量表现为非线性逐渐减小规律; (4) 随着土体变形模量的增加和泊松比的减小, 地表沉降量逐渐减小; (5) 随着土体内摩擦角的增大, 地表沉降量表现为非线性逐渐减小规律。

盾构隧道; 数值分析; 地表变形

当前, 我国的综合国力快速地发展, 城市化进程不断加大, 城市人口急剧增长, 给各大城市的地面交通的通畅性带来了极大的困扰。为了缓解地面交通拥堵的现象, 许多城市不断地在加大规划建设地铁, 地铁线路通常设计在地面以下, 这样就可以与地面的交通相互错开, 不会占用太多地面场地资源。但是, 在建设地铁的同时, 由于地铁隧道通常设计在城市道路的下方, 甚至地铁隧道会紧密地靠近地面的既有构筑物, 地层的不均匀沉降过大会严重威胁到邻近建筑物的正常使用, 更严重的会出现隧道围岩坍塌的情况, 这样就要求地铁隧道在施工时对地层的扰动影响不能太大, 地层的变形控制要求变得极高。

目前, 国内外的许多学者进行了盾构隧道施工对地表变形影响研究, 如孙捷城等[1]和吴昌胜等[2]对地铁盾构隧道施工过程引发的地表变形进行了理论的计算, 考虑了地层损失以及盾壳摩擦力等因素, 得出了盾构施工地表变形的影响规律, 但是没有讨论双线盾构隧道施工地表变形的规律和影响因素; 张治国等[3]通过理论计算与数值模拟对比分析的方法, 考虑地下水以及隧道尺寸对地层变形的影响, 分析了盾构隧道开挖引起的地表变形规律, 得出了地下水位波动幅度对地表沉降影响较大的结论, 但是没有探讨双线盾构隧道存在时的地层变形规律。丁智等[4]和包小华等[5]采用经验理论及数值分析的方法, 研究了双向盾构隧道施工过程注浆层以及地层损失对地表变形的影响, 但未讨论双线隧道施过程中地表变形对土层参数的敏感性; WEI Gang等[6]和PARK[7]采用解析方法分析了双线盾构隧道的地表变形预测方法; 部分学者[8–15]通过理论分析结合室内试验的方法, 探讨了盾构隧道施工对地层变形的影响机理, 得出了盾构隧道施工引起的地表变形的精确计算方法, 但没有讨论双线盾构隧道存在时地层条件参数对地表沉降规律的影响。隧道的埋深以及隧道周边的地质条件直接影响着双线盾构隧道施工后的地表变形量, 基于此, 本文采用数值分析与现场试验相结合的方法, 研究不同施工条件参数下双线盾构隧道施工对地表变形的影响规律, 对后续类似工程施工及施工前风险预测具有一定的参考意义。

1 工程实例

1.1 工程概况及地质环境

本文依托南宁地铁3号线某盾构区间, 该区间隧道设计为两条单洞单线的圆形盾构隧道, 左线隧道施工先于右线隧道, 两条隧道中心线间距为14.0 m, 所选取断面的隧道埋深为15 m, 隧道结构处于圆砾地层。所选取的隧道断面的土层物理力学参数详见表1。

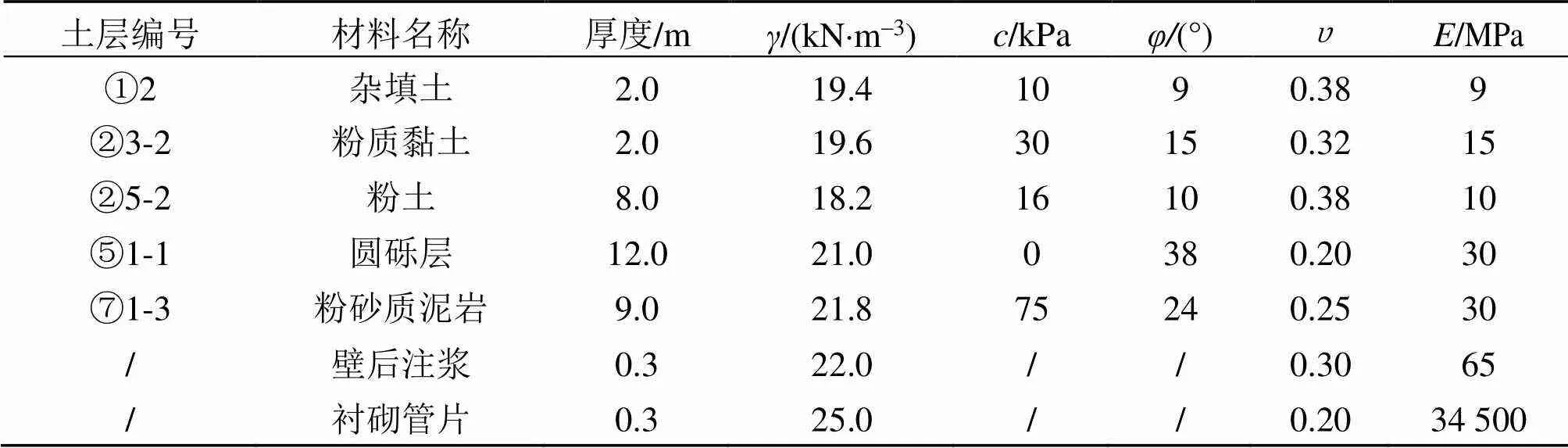
表1 物理力学参数表

注:分别代表材料容重、粘聚力、内摩擦角、泊松比、变形模量。

1.2 现场监测设计

选取本区间地表监控量测的1条典型测线进行分析, 该测线处隧道埋深为15 m, 为了减小三维边界影响, 在所选测线断面往前后各延伸15 m建立数值分析模型。本文所研究的隧道现场施工是左线先于右线, 故不考虑两隧道间纵向错距进尺的影响, 且开挖顺序为左洞贯通后再开挖右洞, 故取左右洞都贯通后的地表变形量进行对比分析。

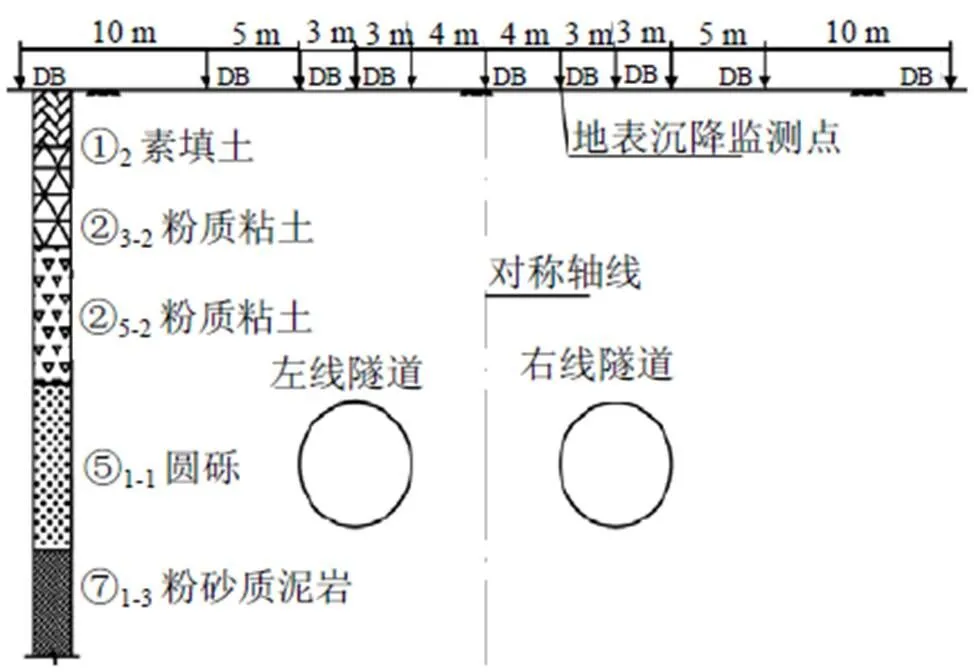
图1 工程概况及地表监测图

1.3 建立数值分析模型

基于上述工程分析情况, 本节采用FLAC3D建立数值分析模型进行研究, 根据圣维南原理确定数值模型中的边界尺寸, 左右边界各取3倍洞径, 下边界取3倍洞径, 上边界取到工程地表, 数值模型水平方向为向, 纵向为向, 竖直方向为向, 建立××=56 m×30 m×39 m数值分析模型。本文所依托的盾构隧道外直径为6 m, 内直径为5.4 m, 盾构隧道支护结构为厚0.3 m, 环宽1.5 m的钢筋混凝土管片, 隧道管片的混凝土强度等级为C50, 数值分析过程中采用弹性本构模型来模拟支护结构。隧道管片的壁后注浆层厚度取为0.3 m, 数值分析过程中通过改变注浆层的材料参数进行模拟隧道外侧的壁后注浆, 采用弹性本构模型来模拟。数值分析模型中土体的应力应变关系选择Mohr-Coulomb本构模型来分析。图2为数值分析网格示意图。

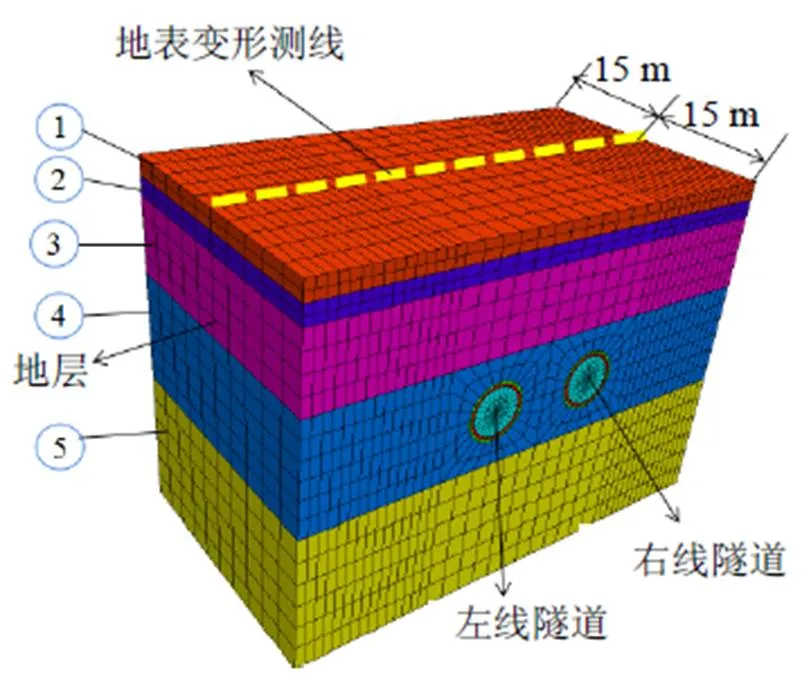
图2 数值分析网格示意图

1.4 施工过程模拟

(1) 建立好模型网格后, 对各个土层分组进行参数的赋值, 在开挖前隧道及注浆层的分组应该赋值为对应的土层参数, 施加重力, 约束模型左右、前后边界和底边界速度为0, 设置求解精度为1e-5, 对模型进行初始平衡, 将初始平衡位移清零;

(2) 使用null命令进行隧道开挖0～6 m, 在隧道掌子面施加均布荷载(现场盾构机土仓压力为120 kPa)模拟盾构机土仓压力, 通过对模型的调试, 采用step为100来模拟隧道开挖尚未进行注浆及管片支护前的应力释放, 之后对壁后注浆层、衬砌管片进行求解计算达到求解精度;

(3) 依次循环第二步操作, 每一次开挖6 m, 直到开挖到达= 30 m断面, 取出监测断面的变形值。

1.5 模型验证

图3为现场实测与数值分析地表沉降量对比图。根据现场实际开挖的顺序, 先开挖左线隧道, 后开挖右线隧道进行数值模拟, 将数值模拟结果与现场实测数据进行对比分析。由图3可知, 从隧道的横向方向分析盾构施工引起的地表沉降呈现出一个沉降槽的形式, 最大沉降量出现在靠近先行隧道一侧, 数值分析得到的横向地表沉降量与现场实测沉降量基本吻合, 两者之间存在最大约2 mm的差别, 这主要是由于现场土层是各向异性的, 而模型中建立的土层单元是横观各向同性的, 且模型中围岩应力释放略大, 同时数值分析中掌子面的土仓压力与实际土层的掌子面侧压力不同而引起的, 但是模型计算结果整体变化趋势与现场实测地表变形规律基本一致, 本数值分析模型基本符合本工程的施工条件。

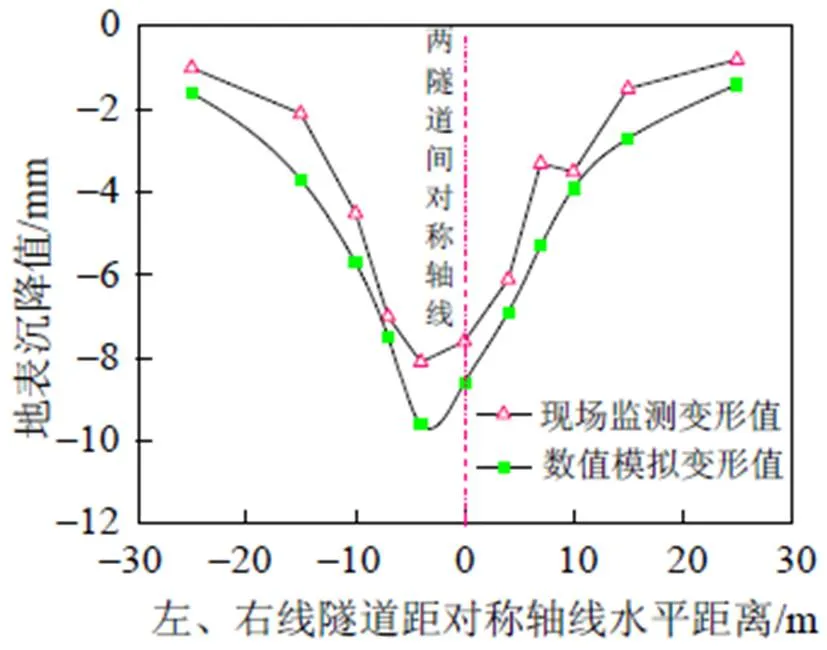
图3 现场实测与数值分析地表沉降量对比图

2 不同施工条件引发地表变形规律分析

2.1 不同土仓压力对地表变形的影响

盾构施工过程中, 土仓压力的大小直接影响着隧道掌子面的稳定性, 从而会影响隧道围岩地层的稳定。因为在均匀地层中, 隧道埋深不变的情况下掌子面的侧向主动土压力基本不变, 因此本节假定盾构机土仓压力与朗肯土压力理论计算得到的掌子面侧向主动土压力之间的比值为R。通过选取R= 0.6、0.8、1、1.2、1.4进行数值分析。图4为不同R值地表变形图, 由图4可知, 当土仓压力小于朗肯理论计算的主动土压力时, 土仓压力对地表的变形影响较为明显, 土仓压力增加20%, 地表变形量减小约10%, 并且在隧道掌子面周围影响较大, 在远离隧道的两侧影响不明显, 当R值大于1以后, 增加土仓压力, 地表变形量的减小效果不明显。

图4 不同PR值地表变形图

2.2 不同埋深对地表变形影响

图5为不同埋深地表变形图。由图5可知, 在相同性质的地层中, 随着隧道埋深的增加, 地表沉降量表现为非线性减小规律。当隧道埋深从12 m增加到15 m, 埋深增加25%, 相比于埋深为12 m时的最大地表沉降量减小3.3 mm, 减小26.2%左右; 当隧道埋深从15 m增加到18 m, 埋深增加20%, 相比于埋深为15 m时的最大地表沉降量减小1.3 mm, 减小13.9%左右; 这主要是由于随着隧道的埋深的增加塌落拱效应逐渐发挥作用而引起的。在双线盾构隧道施工过程中, 先行洞一侧的地表变形量比后行洞一侧的地表变形量大, 这可能是由于后行洞开挖后对土层的扰动在先行洞的一侧造成“群洞叠加效应”引起的。

图5 不同埋深地表变形图

2.3 不同变形模量和泊松比对地表变形影响

变形模量和泊松比是影响土层变形性质的重要参数。图6为不同变形模量和泊松比地表变形图。由图6可知, 双线盾构隧道施工过程中, 横向地表沉降呈现出一个“V型”的沉降槽形式, 最大地表沉降量出现在两隧道之间偏先行洞一侧。减小土体的泊松比, 同时增大土体的变形模量, 地表沉降量表现为非线性减小规律, 当土体的泊松比减小20%, 同时土体的变形模量增加25%, 地表变形减小量最大约为8.6%, 这主要是由于土体的变形模量增加后土体的压缩性减小, 同时泊松比减小后, 土体的强度变大而引起的。说明双线盾构隧道施工过程中可以采取地面注浆加固土体的方法来提高土体的强度, 从而减小地表的变形量。

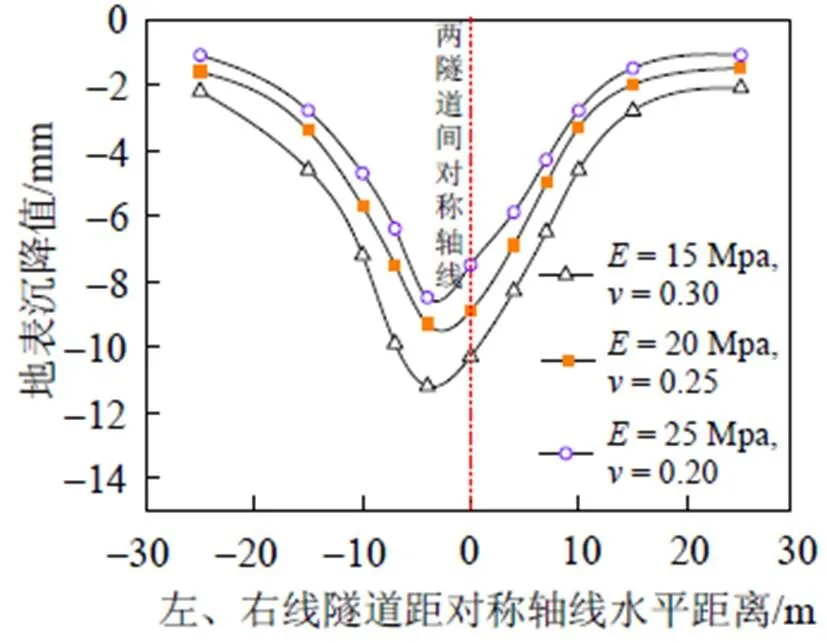
图6 不同变形模量和泊松比地表变形图

2.4 内摩擦角φ对地表变形的影响

图7为不同内摩擦角地表变形图。由图7可知, 随着土层的内摩擦角的增加, 双线隧道横向地表沉降量减小, 在两倍隧道洞径水平范围内地表沉降影响较为显著, 横向地表沉降呈现出一个“V型”的沉降槽形式。当内摩擦角从15°增加到25°, 与内摩擦角15°时比较, 内摩擦角增加66.7%, 最大地表沉降量减小1 mm, 减小10.1%左右; 当内摩擦角从25°增加到35°, 与内摩擦角25°时比较, 内摩擦角增加40%, 最大地表沉降量减小0.7 mm, 减小8.6%左右。当内摩擦角超过25°后, 随着内摩擦角的增大, 横向地表沉降量增量幅度有所减小, 可见在内摩擦角超过25°后, 内摩擦角的变化对横向地表变形量影响减弱, 这主要是由于土层的内摩擦角增大以后, 土颗粒间存在一定相互咬合力而引起的。

图7 不同内摩擦角j地表变形图

3 结论

本文采用数值模拟和现场监测试验相结合的方法, 分析了盾构隧道埋深和隧道周边围岩地层参数以及盾构机推力对双线盾构隧道施工过程中地表变形规律的影响, 主要研究结论如下:

(1) 双线盾构隧道施工过程中, 横向地表沉降呈现出一个“V型”的沉降槽形式, 最大地表沉降量出现在两隧道之间偏先行洞一侧;

(2) 当土仓压力小于朗肯理论计算的主动土压力时, 土仓压力的变化对地表的变形影响较为明显, 土仓压力增加20%, 地表变形量减小约10%;

(3) 在双线盾构隧道施工过程中, 随着隧道埋深的增加, 地表沉降量表现为非线性逐渐减小规律;

(4) 随着土体变形模量的增加, 同时减小泊松比, 地表变形量表现为非线性减小规律; 当变形模量增加25%, 同时泊松比减小20%时, 最大地表变形量减小8.6%;

(5) 随着土体的内摩擦角的增加, 地表沉降量表现为非线性逐渐减小规律; 当内摩擦角从15°增加到25°, 内摩擦角增加66.7%, 最大地表沉降量减小1 mm, 相比于内摩擦角为15°时的最大地表沉降量减小10.1%左右; 当内摩擦角从25°增加到35°, 内摩擦角增加40%, 最大地表沉降量减小0.7 mm, 相比于内摩擦角为25°时的最大地表沉降量减小8.6%左右;

(6) 在双线盾构隧道施工过程中, 影响地表沉降量的参数敏感性从大到小依次为隧道埋深、土体变形模量、土仓压力、土层内摩擦角。

[1] 孙捷城, 路林海, 王国富, 等. 小半径曲线盾构隧道掘进施工地表变形计算[J]. 中国铁道科学, 2019, 40(5): 63–72.

[2] 吴昌胜, 朱志铎, 宋世攻, 等. 软土地层大直径泥水盾构掘进引起的地面变形分析[J]. 岩土工程学报, 2019, 41(z1): 169–172.

[3] 张治国, 师敏之, 张成平, 等. 类矩形盾构隧道开挖引起邻近地下管线变形研究[J]. 岩石力学与工程学报, 2019, 38(4): 852–864.

[4] 丁智, 王凡勇, 魏新江. 软土双线盾构施工地表变形实测分析与预测[J]. 浙江大学学报(工学版), 2019, 53(1): 61–68.

[5] 包小华, 章宇, 徐长节, 等. 双线盾构隧道施工沉降影响因素分析[J]. 重庆交通大学学报(自然科学版), 2020, 39(3): 51–60.

[6] WEI Gang. Prediction of soil settlement caused by double-line parallel shield tunnel construction [J]. Disaster Advances, 2013, 6(6): 23–27.

[7] PARK K H. Analytical solution for tunneling-induced ground movement in clays [J]. Tunnelling and Underground Space Technology, 2005, 20(3): 249–261.

[8] 王晓睿, 姜洪建, 朱坤, 等. 基于土压盾构的城市地铁隧道构筑过程地表沉降规律[J]. 地球科学, 2019, 44(12): 4 293–4 298.

[9] 周杰, 朱贤宇, 唐健. 大断面盾构隧道施工碴土改良数值模拟及土舱压力对地表变形的影响机理研究[J]. 现代隧道技术, 2019, 56(z2): 374–378.

[10] 杨玉平, 刘运思, 牟天光, 等. 基于Mindlin解的盾构隧道施工地表变形及参数敏感性分析[J]. 湖南文理学院学报(自然科学版), 2020, 32(1): 89–94.

[11] 王京涛. 基坑开挖对既有地铁隧道及地表变形影响分析[J]. 湖南文理学院学报(自然科学版), 2019, 31(1): 79–84.

[12] 闫潇, 杨双锁, 刘柄呈, 等. 湖底粉细砂层赋存条件下双线盾构掌子面压力数值研究[J]. 公路, 2020, 65(4): 367–372.

[13] 何祥凡, 高锋, 申兴柱, 等. 盾构隧道穿上软下硬地层掌子面顶推力优化研究[J]. 地下空间与工程学报, 2018, 14(6): 1 603–1 610.

[14] 付亚雄, 贺雷, 马险峰, 等. 软黏土地层盾构隧道开挖面稳定性离心试验研究[J]. 地下空间与工程学报, 2019, 15(2): 387–393.

[15] 肖明清, 门燕青, 孙连勇, 等. 软土盾构隧道纵向应力松弛规律的数值分析[J]. 现代隧道技术, 2018, 55(z2): 544–551.

Study on surface deformation law of double line shield tunnel construction under different construction conditions

Mou Tianguang1, 2, Zhu Jianglin1, 2

(1. Hunan Province Key Laboratory of Geotechnical Engineering for Stability Control and Health Monitoring, Hunan University of Science and Technology, Xiangtan 411201, China; 2. School of Civil Engineering, Hunan University of Science and Technology, Xiangtan 411201, China)

In order to study the law of surface deformation caused by the construction of double-line shield tunnel under different conditions, based on a shield section project of Nanning Metro Line 3, the law of transverse surface subsidence in the construction of double-line shield tunnel is analyzed by numerical analysis and field measured data. The results show that :(1) the surface subsidence shows the form of settlement trough, and the maximum surface subsidence appears on the side of the first tunnel between the two tunnels ;(2) when the silo pressure is less than the active soil pressure of Rankine theory, the silo pressure increases by 20% and the surface subsidence decreases by about 10% ;(3) As the buried depth of the tunnel increases, the surface settlement shows a non-linear and gradually decreasing law ;(4) With the increase of soil deformation modulus and the decrease of Poisson's ratio, the amount of ground settlement gradually decreases ;(5) With the increase of the friction angle in the soil, the surface settlement shows a non-linear gradually decreasing law.

shield tunnel; numerical analysis; surface deformation

U 231

A

1672–6146(2020)04–0075–05

10.3969/j.issn.1672–6146.2020.04.015

牟天光, 1628844370@qq.com。

2020–06–01

国家自然科学基金项目(41172275)。

(责任编校: 张红)