基于磁场FE和CFD的磁流变阻尼器力学性能分析

刘昕运 吴大林 马吉胜

(1.陆军工程大学火炮工程系， 石家庄 050001； 2.西京大学机械工程学院， 西安 710123)

0 引言

磁流变(MR)阻尼器的内部通常填充有特殊的磁流变液体，该液体由非导电液体、微小的铁磁性粉末和少量添加剂混合而成[1]。这种特殊的流体在磁场作用下表现出粘塑性非牛顿流体的特性[2]。流体的屈服应力由磁感应强度决定，即为磁流变阻尼器的阻尼力可控的原因[3]。相比于胶质阻尼器和其他阻尼器[4-5]，MR阻尼器的滞回环范围更大[6]。目前，MR阻尼器发展迅速，已在车辆工程[7-8]、土木工程[9]、医疗器械[10]、飞行器[11]和武器工业[12]等领域被广泛使用。

随着计算机技术的发展，有限元分析(Finite element analysis，FEA)和计算流体动力学(Computational fluid dynamics，CFD)仿真技术已成为分析磁流变液体和磁流变阻尼器的主要手段。与传统的一维解析模型相比，FEA和CFD数值模拟更加准确，且能够获得更多可视化参数[13]。文献[14]在COMSOL中耦合了磁场和流体，并进行了实验和仿真。文献[15-16]在ANSYS/CFX中用CLL语言耦合了磁流变阻尼器模型。文献[17]模拟了磁流变阻尼器的磁场分布，并考虑了温度的影响。以上研究属于边界已知的“显式”主动运动问题，而本文研究的冲击运动属于边界条件不可知的“隐式”被动运动问题。目前，此类问题在国内外尚未见相关研究和报道。

本文提出单向耦合数值模拟方法。首先在COMSOL中对磁场进行有限元分析，然后将磁场结果导入Fluent中，结合Six DOF模型和UDF文件对冲击过程进行分析，通过实验进行验证，以期准确获取磁流变阻尼器的力学特性。

1 数值模型

1.1 结构原理

图1 磁流变阻尼器CAD设计图Fig.1 CAD design of MR damper

近年来，磁流变阻尼器出现了多种结构，单出杆式[18]和双出杆式[19]，有气体腔[20]和无气体腔[21]，特殊式[22]等。本文涉及的MR阻尼器用于缓冲舰炮系统中的高速运动的实验弹，CAD设计如图1所示。由于外部几何限制，对阻尼器结构进行了特殊设计，如图2所示，主要由活塞杆、磁流体活塞、空气弹簧活塞、缸体、限位块、线圈、压缩空气、磁流变液组成。活塞杆两端直径相等，弹性回复力主要来自空气压缩。活塞中绕有两组线圈，其被外壳密封。导线从活塞杆内部通过并连接外部直流电源。当线圈通电时，将产生大致如图2所示的磁场分布。磁场导致磁流变液中的铁磁固体颗粒按磁感线形成链状，导致环形间隙中的部分流体表现出极大的屈服应力，流体通过间隙时会产生较大的阻尼力。阻尼器主要尺寸如表1所示。

1.2 静磁场FE模型

有限元模型在多物理场仿真软件COMSOL/Multiphysics中建立。依据麦克斯韦方程组[10]计算电磁场，包括恒定电荷密度的连续性方程、安培定律和法拉第定律，即

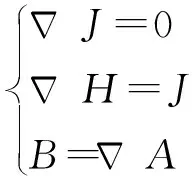
(1)

其中

B=μoμrH

(2)

式中H——磁场强度

J——电流密度

A——磁矢量势

B——磁通密度

μr、μo——材料磁导率、真空磁导率

根据阻尼器的对称性，生成二维轴对称网格，如图3所示。计算域总共有70 375个四边形网格单元。为了评估网格的相关性，生成另一组更加细密的网格，共281 500个四边形单元。比较两组网格的磁通强度计算结果，输出曲线几乎相同。这说明生成的网格已经非常精细，结果误差与网格尺寸基本无关。

图3 磁流变阻尼器的有限元网格Fig.3 FE mesh of MR damper

采用LORD公司的MRF-140CG型磁流变液，图4为该磁流变液的特性曲线。活塞头和缸体采用碳素结构钢1045，活塞杆采用低磁导率金属。线圈导线采用美国线规AWG 24标准铜线。部分材料参数如表2所示。

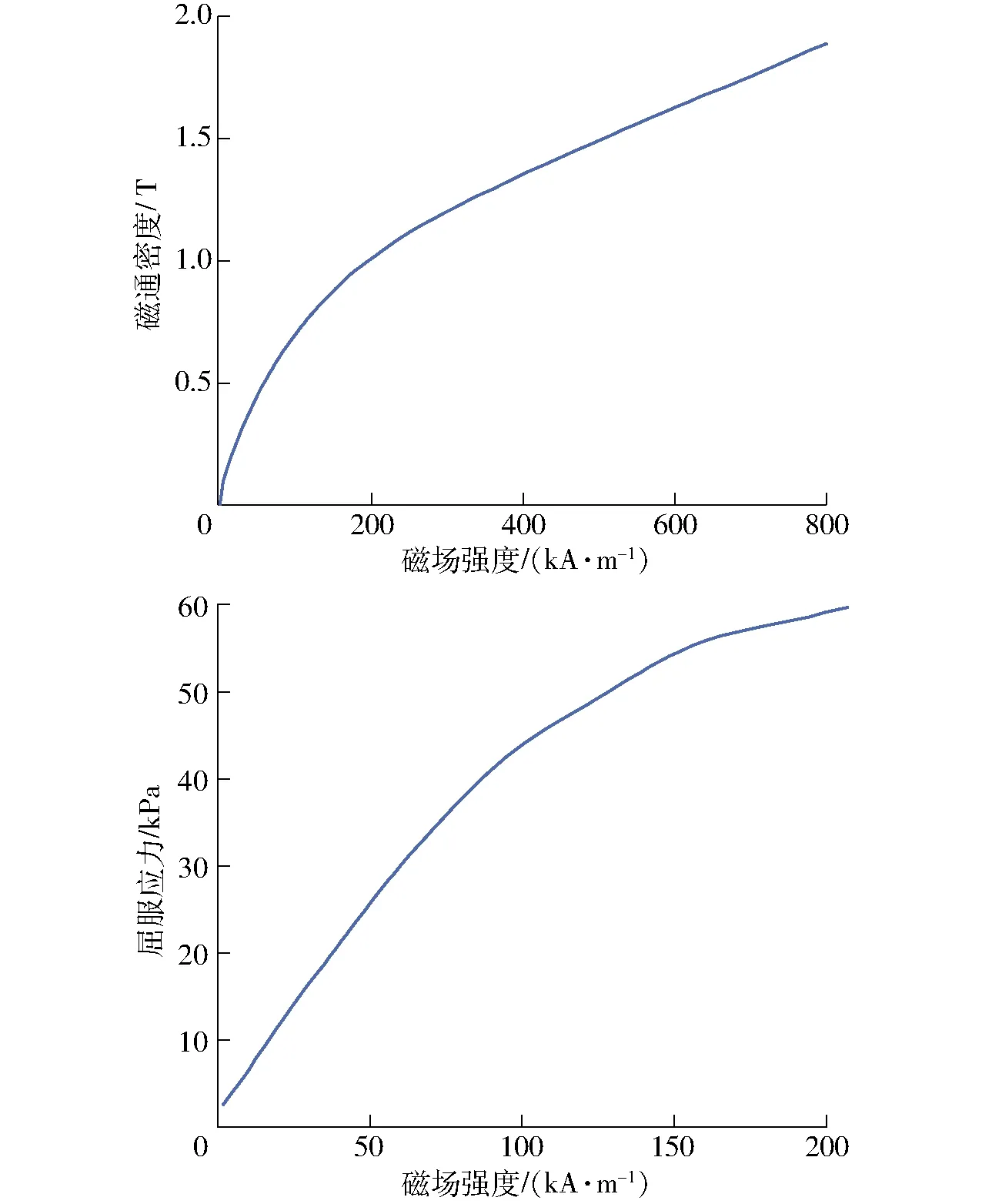
图4 MRF-140CG型磁流变液的特性曲线Fig.4 Characteristics of MRF-140CG MR fluid

1.3 磁流变液CFD模型

MR阻尼器的CFD分析需考虑湍流和能量传递，其中流体控制方程包括连续性方程、Navier-Stokes方程和能量方程[23]

表2 材料属性参数Tab.2 Material property parameters

(3)

式中ρ——流体密度V——流体速度

fb——体积力p——差压

μ——动力粘度h——比焓

λ——热导率Φ——粘性耗散项

Sh——源项T——温度

1.3.1流体本构模型

根据图4中磁流变液材料属性定义磁通密度B和屈服应力τy的关系曲线。使用Hill sigmoidal函数拟合为

(4)

式中，ε=117 024.8，β=0.967 66，k=1.693 63。

目前，针对粘塑性流体提出了多种本构模型[24-26]。本文采用由双曲正切函数定义的流变粘度模型[13-14]，即

(5)

式中α——粘度增长控制因子，取0.03

ζ——粘度增长控制因子，取0.1

对速度冲击过程进行CFD分析时，必须考虑MR流体的可压缩性。因为阻尼器在冲击瞬间压力变化非常大，如果不考虑流体的压缩性将导致压力计算出现异常。液体压力用Tait状态方程描述，即

(6)

式中m——密度指数ρ0——参考密度

E0——参考体积模量

1.3.2空气弹簧

磁流变阻尼器有空气弹簧结构，空气腔存在一定初始压力，其主要作用是提供回复力，使被压缩的阻尼器自动复位。空气弹簧力Fs一般依据气体多变过程方程来描述，即

(7)

式中p0——初始压力，取2.5 MPa

Aair——活塞面积，取1 756.15 mm2

W0——初始体积，取52 684.5 mm3

n——气体多变指数，取1.3

x——活塞位移

1.3.3流体网格定义

流体计算域仍然采用二维轴对称四边形网格。动网格使用Layering层铺技术，网格被压缩至一定程度时，贴近壁面的网格会坍缩与合并。而网格被拉伸至一定程度时，贴近壁面的网格会分裂出新层。为了顺利实现网格层铺法，在生成网格时需考虑Mesh Interface。如图5所示，活塞两侧的壁面被定义为刚体移动壁面。仅生成流体域网格，间隙处的网格被加密，总共包含了95 403个四边形单元。

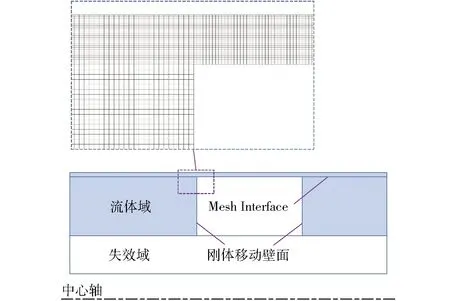
图5 流体网格定义示意图Fig.5 Schematic of fluid mesh definition

1.3.4用户自定义函数

磁流变阻尼器的活塞移动时，磁场的影响区域会跟着变化。所以，对于非牛顿区域的跟踪和捕捉是必要的。与显式边界模型不同，隐式边界模型的“磁场作用区域”不能直接定义，其需要依赖移动壁面的实时坐标。因此，基于C语言编写了用户自定义函数(UDF文件)，并在求解器中进行编译。

使用“DEFINE_PROPERTY”宏定义计算域的动力粘度属性。首先，使用“Get_Domain”宏和“Lookup_Thread”宏获取移动壁面的指针，在此之上用“F_CENTROID”宏访问移动壁面的坐标信息并存入数组；然后写入式(4)、(5)和磁场FE分析得到的磁通密度。以上函数中涉及2个变量，其中坐标信息从数组中提取，剪切速率由“C_STRAIN_ RATE_MAG”宏访问得到；最后用“C_ CENTROID”宏访问计算域的所有网格单元，并把非牛顿粘度函数赋值于受磁场影响的单元。

活塞只在x方向移动，而且存在空气弹簧力和限位块，故还需要定义6自由度模块的UDF文件。根据头文件six_dof.h，使用“DEFINE_SDOF_PROPERTIES”宏定义刚体属性，代码可以与属性宏编写到一个文件中。使用“SDOF_MASS”宏定义刚体的质量，其值取阻尼器负载的质量；使用“SDOFO_1DOF_T_P”宏定义自由度为1个平移自由度；使用“SDOFO_LOC， SDOFO_MIN，SDOFO_MAX”宏定义刚体的位移限制；最后用“SDOF_LOAD_F_X”宏写入空气弹簧力式(7)。

2 数值结果

对于单向耦合模型，式(4)、(5)是耦合磁场FEA和CFD的关键。通过静磁场分析得到磁通密度B在流体域的分布，然后将其转换为动力粘度在流体域的分布，并导入CFD模型。

2.1 静磁场FE分析

当输入电流I=4.0 A时，计算域内的磁通密度等值线如图6所示。大部分磁感线从活塞的两端穿过流体进入阻尼器的缸体，由于流体和活塞杆的磁导率都非常低，磁通量更多地分布在磁性材料中。输出环形间隙中间线上的磁通密度分布曲线如图7所示，磁通密度存在两个峰值，分别在环形间隙的两端，最大值达到1.96 T。而在两个峰值的中部以及外侧，磁通密度迅速降低至接近0。

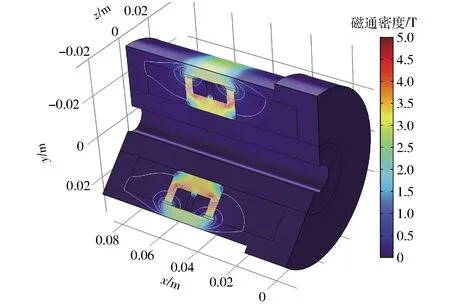
图6 流体域中的磁通密度分布Fig.6 Magnetic flux density distribution in computational domain

图7 环形间隙中线上的磁通密度分布Fig.7 Magnetic flux density distribution on middle line of annular gap

2.2 模型验证

模型采用瞬态压力基求解器(PBS)。使用Realizablek-ε模型，激活能量方程和粘性热。设置Coupled算法并采用二阶离散格式，求解控制Courant数为50，最大求解时间步长为1×10-5s。

磁通强度在流体中的主要作用区域如图8所示。受磁场影响的主要区域不全在环形间隙中，间隙的两端存在溢出。可能会影响阻尼器的力学特性计算结果。因此，在UDF代码中编写环形间隙两端的“圆弧”区域，其结合图7的磁通密度分布曲线能够更准确地描述非牛顿粘度。

图8 环形间隙两端的圆函数区Fig.8 Circular function area at both ends of annular gap

在CSS-55100型万能试验机上对阻尼器进行匀速准静态运动实验，如图9所示。固定缸体，对活塞杆进行匀速的加载和卸载。利用压力传感器和位移传感器采集阻力和位移。图10、11分别为匀速准静态运动的阻抗力-时间曲线和滞回曲线。对比阻尼器的实验和仿真曲线，验证了模型的准确性。

图9 匀速准静态实验设备Fig.9 Uniform quasi-static experimental equipment

图10 匀速准静态运动的阻抗力-时间曲线Fig.10 Resistance-time curves of uniform quasi-static motion

图11 匀速准静态运动的滞回曲线Fig.11 Hysteresis loop of uniform quasi-static motion

2.3 冲击CFD分析

当刚体初速度为7.4 m/s，壁面边界的运动状态由流固双向耦合的6自由度模块自动解算，总仿真时间为80 ms时，整个冲击过程的等值线和流线图如图12所示。冲击初期，流体在环形间隙中瞬时最大速度达到了75 m/s以上，但随着动能的耗散，流体速度会很快降低，达到最大位移仅需4 ms。磁流变阻尼器在运动过程中，流体产生了许多不停变化的涡，且流线极为不规则。但较大的涡都出现在活塞运动方向的后面。

阻尼器吸收的动能主要转化为流体热能。由于液体具有粘性，内部摩擦将产生热量，初始温度为300 K时，流体温度分布如图13所示。高温液体主要产生于环形间隙，因为此处剪切速率和动力粘度最大。冲击运动结束时温度分布并不均匀，活塞一侧的平均温度暂时高于另一侧。

输出的磁流变阻尼器运动学特性曲线如图14所示。MR阻尼器的压缩过程持续4 ms，拉伸过程持续大约70 ms。图14a显示，MR阻尼器最终无法完全复位，在位移为1.3 mm处几乎停止运动，这是由Bingham流体性质决定的。阻尼器在复原运动时，流体域的剪切速率逐渐降低。由式(5)可知，在剪切速率很低时，表观粘度会逐渐大幅升高，从而导致流体剪切应力变大。而随着位移行程的减小，空气弹簧力逐渐降低。当空气弹簧力小于流体阻力时，活塞开始减速直到停止运动。阻尼器在复原运动阶段先加速后减速的特征如图14b所示。在实际应用中，这种现象并不会影响磁流体阻尼器的使用。

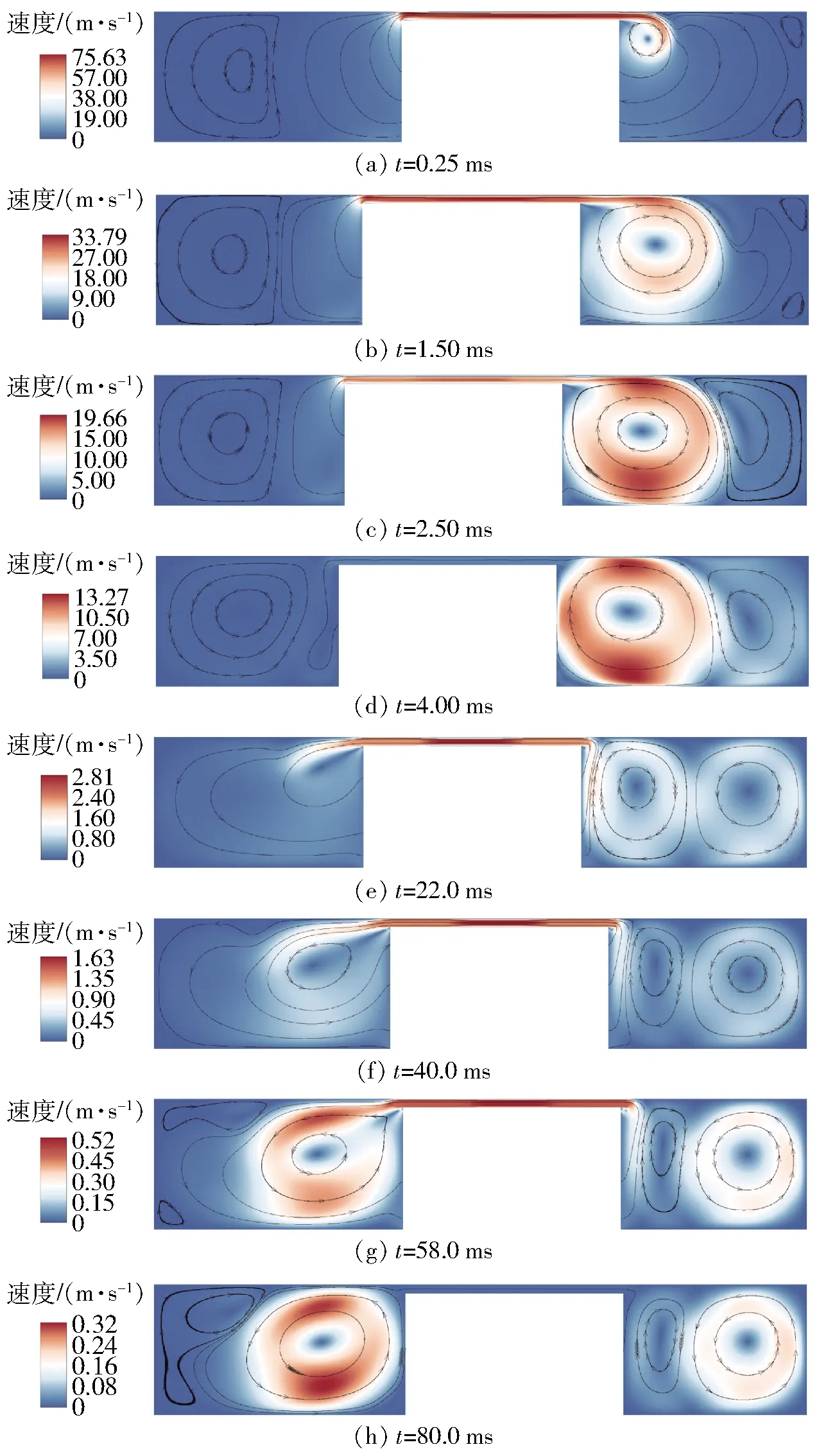
图12 磁流变阻尼器速度等值线和流线Fig.12 Velocity contours and streamtraces of MR damper

图13 磁流变阻尼器温度等值线Fig.13 Temperature contours of MR damper

图14 冲击运动的运动学特性曲线Fig.14 Kinematic characteristic of impact motion

这是由于当控制电源断开后，磁流变液会恢复牛顿流体特性，阻尼器将很快完全复位。图15为冲击运动的滞回曲线，阻尼器的阻抗力曲线变化非常不规则，最大阻抗力出现在冲击初期，在行程2 mm处达到最大阻抗力110 kN，而后迅速降低并逐渐趋于平稳。复原阶段中的阻抗力保持在200～400 N极低的水平。该磁流体阻尼器在冲击过程中几乎吸收了所有的初始动能，其缓冲效能较为优异。

图15 冲击运动的滞回曲线Fig.15 Hysteresis loop of impact motion

3 结论

(1)针对某磁流变阻尼器提出了结合磁路有限元分析和计算流体动力学分析的单向耦合仿真研究方法。在实验验证匀速准静态运动模型的基础上，对模型进行了特定冲击载荷的流固双向耦合模拟，获得了其力学特性规律。

(2)在隐式边界条件的CFD分析中，解决了粘塑性流体本构定义、非牛顿粘度区的跟踪和捕获、以及被动运动的动网格处理等难点。在磁路FE分析得到双峰分布的磁通密度的基础上，用双曲正切函数定义了粘塑性磁流变液的非牛顿粘度，并用“圆函数”准确捕获非牛顿粘度区。模型也考虑了液体的可压缩性和多变方程描述的空气弹簧力。

(3)在冲击运动过程中，流体域产生大小不一的多个涡，其中最明显的涡产生于活塞运动方向的后侧。磁流变液中的热量主要产生于环形间隙，最终在活塞一侧的平均温度高于另一侧。在持续供电的情况下，阻尼器将无法完全复位，但电路控制可以解决这一问题。