考虑压力效应的液压缸摩擦模型研究

李毅波 曾云龙 潘 晴，2 姜雪鹏

(1.中南大学轻合金研究院, 长沙 410083； 2.浙江大学流体动力与机电系统国家重点实验室， 杭州 310027)

0 引言

液压缸因具有驱动力大、功重比大、响应快、操纵方便、可自动实现过载保护等优点而广泛应用于各种工业设备中。在含有伺服阀控液压缸的液压系统中，非线性摩擦力是影响液压系统位置和速度控制精度的主要因素，而摩擦力来源于液压缸的往复运动密封界面，与运动速度、液压油压力等因素密切相关。因此，国内外研究者针对摩擦力建模进行了大量研究。

为了消除摩擦力对液压伺服系统的不良影响、提高液压系统控制性能，国内外研究学者进行了大量的摩擦科学实验。Stribeck模型[1]能描述低速时摩擦力随速度增加而减小、高速工况摩擦力随速度增大而增大的现象,故广泛应用于控制系统[2-5]中，并且控制精度得到显著提高。进一步研究发现，Stribeck摩擦模型在预测稳态摩擦力时比较理想，但预测动态摩擦力则不太理想[6]。LuGre模型[7]将两个相互运动物体的接触部分表征为鬃毛模型，该模型能很好地预测摩擦滞后、Stribeck效应、预滑动阶段等摩擦特性，被广泛应用于摩擦补偿控制系统[8-9]。TRAN等[10]针对液压系统实际情况，建立了考虑负载变化、油膜厚度和时间参数的改进LuGre摩擦模型,该模型能很好地预测摩擦滞后、Stribeck效应、预滑动阶段等摩擦特性，与经典LuGre摩擦模型相比，预测能力更强。PAN等[11]在文献[10]基础上，考虑了油膜厚度的非线性特性，引入了Bouc-Wen模型，在伺服液压系统中使用柱塞式液压缸实验对模型进行验证，进一步提高了摩擦力预测精度。在LuGre模型后，AL-BENDER等[12]提出了GMS(Generized Maxwell slip)摩擦模型，该模型具有较强的摩擦力预测能力，主要表现在对摩擦滞后、预滑动阶段和Stribeck效应等摩擦特性具有更加准确的描述能力。BOEGLI等[13]提出了Smoothed-GMS模型，该模型使用基于梯度的微分方程衔接摩擦过程中的预滑动阶段和滑动阶段。NILKHAMHANG等[14]提出基于线性Stribeck模型的GMS模型进行自适应摩擦补偿，并验证了模型的有效性。KANG等[15]改进了GMS摩擦模型，针对电液伺服系统中存在的不确定性干扰和非线性摩擦力，设计了自适应滑模控制器，进行了摩擦补偿控制实验，取得了较高的力跟踪控制精度。倪风雷等[16]基于速度观测器进行了GMS参数辨识，并基于GMS模型进行摩擦补偿，得到了较好的位置控制精度。

液压系统中液压缸的摩擦力主要来源于活塞密封件与液压缸缸体的相互作用。密封件形变对液压缸摩擦力有显著影响，而液压缸油腔内油压会影响密封件的形变，进而影响密封件与活塞杆和缸体的接触状态，从而影响摩擦力的变化。在实际液压伺服控制系统中，大部分学者直接采用经典的摩擦模型进行摩擦补偿控制[17-26]，很少考虑液压系统中油压对摩擦力的影响。本文提出考虑压力效应的稳态摩擦模型和动态摩擦模型，搭建用于验证液压缸摩擦模型预测效果的摩擦力测试实验台，研究复杂工况下液压缸稳态摩擦特性和动态摩擦特性，提出摩擦模型的摩擦参数辨识算法。

1 液压缸摩擦特性实验平台构建

液压缸摩擦力测试实验台如图1所示。在被测油缸的进油口和出油口处均安装压力传感器(ATOS，E-ART-8/250/I型)，用以测量被测缸压力。液压缸活塞运动位移由安装在液压缸同一运动方向的位移传感器(MTS, RPM0800MD601V61型)测得，运动速度由位移信号经滤波后进行差分获得。通过伺服阀(ATOS,DLHZO-TEB-SN-NP-060-L71/I型)来控制进入被测油缸的流量，从而实现调速。实验台位移信号的输出端口、压力传感器输出端口经过PLC S7-1200数据采集模块送入上位机，在后台进行数据处理并存储。实验台测控软件编程环境基于LabVIEW软件平台，控制系统采用速度闭环PID控制，调速范围可达0.5～100 mm/s，可以实现正弦、三角波或者常值跟踪速度下的液压缸摩擦力测试。实验平台的液压控制系统原理图如图2所示。

图1 摩擦力测试实验平台Fig.1 Experiment platform of friction test1.位移传感器 2.液压缸 3.压力传感器

图2 液压缸控制系统Fig.2 Hydraulic cylinder control system

根据牛顿第二定律，运动部件液压缸活塞的运动学方程表示为

Fr=p1A1-p2A2-mg-ma

(1)

式中m——运动部件质量

Fr——液压缸摩擦力

p1——被测液压缸下腔压力

p2——被测液压缸上腔压力

A1——被测液压缸下腔活塞有效面积

A2——被测液压缸上腔活塞有效面积

g——重力加速度

a——加速度

使用卡尔曼滤波器处理位移信号得到加速度a，因而根据式(1)可测得摩擦力。当以正弦信号为速度跟踪信号(速度v为-5～5 mm/s，频率f=0.5 Hz)时，测得的实验数据如图3所示。

图3 动态摩擦力测试实验结果(f=0.5 Hz)Fig.3 Experiment sample of dynamic friction(f=0.5 Hz)

为了验证液压缸上下油腔压力和液压缸密封形式对摩擦特性的影响，采用3种不同密封形式(U形：活塞杆和活塞处皆为U形密封；T形:活塞杆处为U形密封，活塞处为组合密封;G形:活塞杆处为U形密封，活塞处为格莱圈密封)液压缸进行实验，并且还考虑了液压缸缸径和负载特性对摩擦特性的影响，使用的液压缸种类如表1所示，所有液压缸行程为250 mm。

表1 液压缸种类Tab.1 Types of hydraulic cylinder

所有实验均在常温、供油压力恒定(8.0 MPa)工况下进行。分别研究了稳态摩擦力特性和动态摩擦力特性在复杂工况下的变化规律。

2 液压缸摩擦模型

2.1 GMS摩擦模型

GMS摩擦模型如图4所示。该模型能描述3个基本现象：①常速下的Stribeck曲线。②预滑动阶段的不具有本地记忆的滞回效应。③滑动阶段的摩擦滞后。该模型提高摩擦力预测精确性[14]，摩擦力表示为

(2)

式中N——等效摩擦单元数量

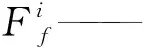
σ2——粘性摩擦系数

图4 GMS摩擦模型Fig.4 GMS friction model

当摩擦单元处于粘滞状态时，独立单元摩擦力为

(3)

式中ki——摩擦单元刚度

当摩擦单元处于滑动状态且液压缸速度大于零时，独立单元摩擦力为

(4)

(5)

式(4)中Stribeck曲线为

(6)

式中Fc——库仑摩擦力αi——单元权重

C——引力系数vs——Stribeck速度

Fs——最大稳态摩擦力

2.2 考虑压力效应的摩擦模型

2.2.1稳态摩擦模型

提出了考虑液压缸进出油口压力的稳态摩擦模型(P-Stribeck)，因为液压缸摩擦力主要来源于密封件与活塞杆和活塞与液压缸内壁的相互作用，并且油腔压力增大会影响密封件形变，进而加强密封件与活塞杆相互作用，影响摩擦特性，为了改进Stribeck摩擦模型，因此引入有杆腔和无杆腔压力影响系数表征油液压力的影响。该模型表达式为

(7)

(8)

式中Kpr1、Kpr2——压力系数

Fpr——压力对摩擦力影响项

Fsp——考虑压力效应的稳态摩擦力

pa——压力，取0.1 MPa

2.2.2动态摩擦模型

结合文献[11-12，14]和式(8)提出了考虑液压缸进出油口压力的动态摩擦模型(P-GMS)。文献[11-12]通过分析液压缸密封油膜动力学和密封界面非定常流体动力学发现，动态摩擦力模型摩擦力相对于速度变量具有相位超前特征，因此在LuGre模型摩擦力项中加入速度一阶微分环节，即活塞运动加速度，以表征运动加速度对摩擦力的影响。为此，本文动态摩擦模型计及加速度和压力效应的双重因素影响，提出了摩擦力预测方法，即

(9)

式中FDP——考虑压力效应的动态摩擦力

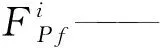
T——流体润滑动态摩擦时间常数

3 摩擦模型参数辨识

以多种工况下的液压缸摩擦力测试实验数据为基础，对所提出的摩擦模型进行参数辨识。参数辨识过程分为2个步骤，首先使用遗传算法辨识稳态摩擦参数，再使用稳态摩擦参数辨识动态摩擦参数。

3.1 稳态摩擦参数辨识

当液压缸在垂直方向上匀速稳定状态下运动时，使用PID控制器保证速度的跟踪精度，使液压缸在给定速度(1、5、10、15、20、25、30、35、40 mm/s)下运行，并采集实验的位移、速度、压力等数据。液压缸缸径40 mm、负载720.3 N、U形密封液压缸稳态摩擦参数辨识结果如表2所示，辨识效果如图5所示。

表2 稳态摩擦参数辨识结果Tab.2 Identification result of steady state

图5 稳态摩擦力辨识结果Fig.5 Identification result of steady steady state friction

3.2 动态摩擦参数辨识

为了辨识GMS摩擦模型动态参数刚度ki和权重αi，采用小幅值的正弦信号进行实验，同样也是采用PID控制器进行速度跟踪，获得实验数据后经过辨识得动态摩擦参数。

将GMS摩擦模型的单元块设置为3个，即N=3，可得到不同实验条件下与之相对应的刚度ki(i=1,2,3)和αi(i=1,2,3)，将辨识得到的GMS摩擦模型参数代入P-GMS模型中辨识P-GMS模型的压力参数Kpr1、Kpr2、T。液压缸直径40 mm时动态摩擦参数辨识结果如表3所示，参数C=0.054 7 N/s，Kpr1=12.96，Kpr2=-13.12,T=1.204。

表3 动态摩擦参数辨识结果Tab.3 Identification result of dynamic state

4 摩擦模型预测效果与实验结果对比

4.1 稳态摩擦特性

4.1.1不同缸径、不同负载下的稳态摩擦特性

采用3种不同缸径(40、80、100 mm)、同等密封形式液压缸，在特定速度(15 mm/s)、相同负载(720.3、1 440.6、2 160.9 N)、泵出口压力恒定(8.0 MPa)工况下进行实验。

如图6所示，在负载720.3 N、速度15 mm/s实验条件下，测得不同缸径液压缸的实验数据并与Stribeck、P-Stribeck模型预测结果进行对比，参数辨识结果如表4所示；由图6可得，本文所提出的摩擦模型预测效果明显优于Stribeck模型。

图6 恒定速度、不同缸径下摩擦力辨识结果对比(U形密封，速度15 mm/s负载720.3 N)Fig.6 Comparison results of friction identification at constant velocity with different diameters (U-seal,velocity 15 mm/s, load 720.3 N)

表4 不同缸径下稳态摩擦参数辨识结果(速度15 mm/s，负载720.3 N)Tab.4 Identification result of steady state (velocity 15 mm/s, load 720.3 N)

采用文献[12]NRMSE误差分析方法,计算式为

图7 恒定速度、不同负载下摩擦力辨识结果对比(缸径100 mm，速度15 mm/s)Fig.7 Comparison results of friction identification at situation of constant velocity with different loads (diameter 100 mm, velocity 15 mm/s)

(10)

式中RMSE——均方根误差

NRMSE——正则化均方根误差

表5为采用NRMSE误差分析方法对负载720.3 N、速度15 mm/s、供油压力8.0 MPa工况下液压缸摩擦力辨识进行的误差分析结果，结果表明，P-Stribeck模型在负载720.3 N、驱动速度15 mm/s工况下3种缸径(40、80、100 mm)U形密封液压缸稳态摩擦力预测的NRMSE分别为2.80%、1.55%、0.86%，其预测精度优于经典Stribeck模型，该模型对该工况下液压缸摩擦力预测是有效的。

表5 不同缸径下Stribeck和P-Stribeck模型摩擦力预测误差分析结果(速度15 mm/s，负载720.3 N)Tab.5 Error analysis of friction prediction between Stribeck model and P-Stribeck model (velocity 15 mm/s, load 720.3 N) %

在缸径100 mm、速度15 mm/s实验条件下，不同负载工况的摩擦力预测结果如图7所示，参数辨识结果如表6所示。从图7中可知，本文所提出的稳态摩擦模型预测效果明显优于Stribeck模型。

表6 不同负载下稳态摩擦参数辨识结果(缸径100 mm，速度15 mm/s)Tab.6 Identification result of steady state (diameter 100 mm, velocity 15 mm/s)

表7为采用NRMSE误差分析方法对不同负载(720.3、1 440.6、2 160.9 N)、速度15 mm/s、供油压力8.0 MPa工况下液压缸力辨识进行误差分析的结果，结果表明P-Stribeck模型在3种负载(720.3、1 440.6、2 160.9 N)、运动速度15 mm/s、缸径100 mm工况下，U形密封液压缸稳态摩擦力预测的NRMSE分别为0.86%、1.25%、1.43%，该模型摩擦力预测精度高于Stribeck模型，P-Stribeck模型对预测该工况下液压缸摩擦力有效。

表7 不同负载下Stribeck和P-Stribeck模型摩擦力预测误差分析(缸径100 mm，速度15 mm/s)Tab.7 Error analysis of friction prediction between Stribeck model and P-Stribeck model (diameter 100 mm, velocity 15 mm/s) %

4.1.2不同密封形式下的稳态摩擦特性

采用3种不同密封形式、相同缸径(100 mm)液压缸，在特定速度(15 mm/s)、相同负载(720.3 N)、泵出口压力恒定(8.0 MPa)工况下进行实验。

如图8所示，测得不同密封形式液压缸实验数据与摩擦力预测效果比较，参数辨识结果如表8所示。由图8可得，本文所提出的稳态摩擦模型预测效果明显优于Stribeck模型。

表9为采用NRMSE误差分析方法对负载720.3 N、速度15 mm/s、供油压力8.0 MPa工况下液压缸摩擦力辨识进行误差分析的结果，结果表明，P-Stribeck模型在负载720.3 N、运动速度15 mm/s、缸径100 mm工况下3种密封形式液压缸稳态摩擦力预测的NRMSE分别为0.86%、0.27%、0.46%，该模型摩擦力预测精度高于Stribeck模型，P-Stribeck模型对预测该工况下液压缸摩擦力有效。

图8 恒定速度、不同密封形式下摩擦力辨识结果对比(缸径100 mm，速度15 mm/s，负载720.3 N)Fig.8 Comparison results of friction identification with different sealing types at constant velocity (diameter 100 mm, velocity 15 mm/s, load 720.3 N)

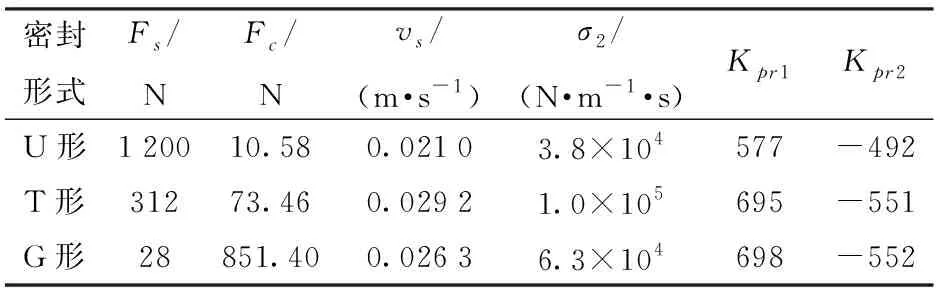
表8 不同密封形式下稳态摩擦参数辨识结果(缸径100 mm,速度15 mm/s，负载720.3 N)Tab.8 Identification result of steady state (diameter 100 mm, velocity 15 mm/s, load 720.3 N)

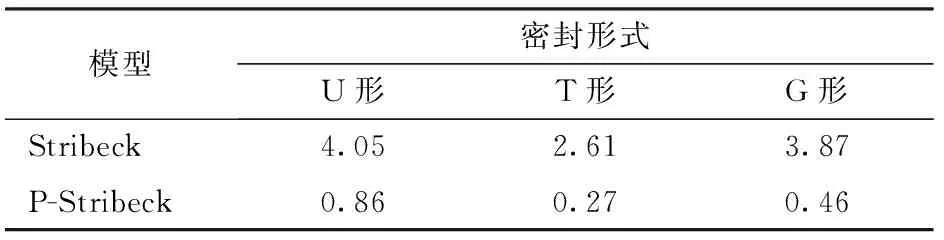
表9 不同密封形式下Stribeck和P-Stribeck模型摩擦力预测误差分析(缸径100 mm,负载720.3 N，速度15 mm/s)Tab.9 Error analysis of friction prediction between Stribeck model and P-Stribeck model (diameter 100 mm, load 720.3 N, velocity 15 mm/s) %

4.2 动态摩擦特性

采用特定缸径(80 mm)、U形密封液压缸，在不同加速度(2、4、6 mm/s2)、周期恒定(8 s)、特定负载(720.3 N)、泵出口压力恒定(8.0 MPa)工况下进行实验。表10为摩擦参数辨识结果,实验速度为10、11、12、13、14、15 mm/s。

表11为不同加速度下GMS和P-GMS两种摩擦模型摩擦参数辨识结果。图9为基于表11摩擦参数的GMS和P-GMS两种摩擦模型预测结果与实验数据的对比结果。由图9可知，本文提出的模型预测效果优于GMS模型预测效果。

表10 动态摩擦参数辨识结果(缸径80 mm)Tab.10 Identification result of dynamic friction force (diameter 80 mm)

表12为采用NRMSE误差分析方法对负载720.3 N、不同加速度(2、4、6 mm/s2)、供油压力8.0 MPa工况下液压缸摩擦力辨识结果，结果表明P-GMS模型在工况为720.3 N，缸径100 mm，不同加速度下U形密封液压缸动态摩擦力预测的NRMSE分别为3.34%、2.89%、3.23%，其预测精度优于GMS模型，该模型对该工况下摩擦力预测有效。

表11 三角波式信号摩擦参数辨识结果Tab.11 Identification result of friction with triangle wave signal

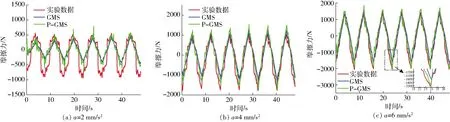
图9 不同加速度下摩擦模型预测结果与实验数据对比(U形密封,缸径80 mm,负载720.3 N)Fig.9 Comparison results between model prediction and friction measured at different accelerations (U-seal, diameter 80 mm, load 720.3 N)

表12 不同加速度下GMS和P-GMS模型摩擦力预测误差Tab.12 Error of friction prediction between GMSmodel and P-GMS model %

采用特定缸径(40 mm)、U形密封液压缸，在不同频率(1.0、2.0 Hz)、特定负载(720.3 N)、泵出口压力恒定(8.0 MPa)工况下进行实验。

表13为不同频率下GMS和P-GMS两种摩擦模型摩擦参数辨识结果。不同频率下实验数据与GMS和P-GMS两种摩擦模型预测结果对比结果如图10所示，由图10可知，本文所提出模型预测效果优于GMS模型预测效果。

表14为采用NRMSE误差分析方法对负载720.3 N、不同频率(0.5、1、2 Hz)、供油压力8.0 MPa工况下液压缸摩擦力辨识结果，结果表明P-GMS模型在工况为720.3 N、缸径100 mm、不同频率下，U形密封液压缸动态摩擦力预测的NRMSE分别为7.37%、7.71%、10.92%，其预测精度优于GMS模型，该模型对该工况下摩擦力预测有效。

表13 动态摩擦参数辨识结果(负载720.3 N)Tab.13 Identification result of dynamic state(load 720.3 N)

5 结论

(1)搭建了一种变负载变速度驱动下液压缸非线性摩擦特性测试实验平台，在不同密封形式、不同缸径、不同负载、不同加速度和频率下对液压缸稳态和动态摩擦特性进行了测试。

图10 不同频率下摩擦模型预测结果与实验数据对比(U形密封,缸径40 mm,负载720.3 N)Fig.10 Comparison results between model prediction and friction measured under different frequencies (U-seal, diameter 40 mm, load 720.3 N)

表14 不同频率下GMS和P-GMS模型摩擦力预测误差Tab.14 Error of friction prediction between GMSmodel and P-GMS model %

(2)基于Sribeck和GMS模型，建立了考虑液压缸油腔压力和运动加速度的稳态摩擦模型和动态摩擦模型，提出了一种改进摩擦模型的摩擦参数辨识方法。

(3)采用Stribeck和P-Stribeck两种模型预测稳态摩擦力，并与实验数据进行对比，结果表明，P-Stribeck模型预测3种负载液压缸摩擦力NRMSE

分别为0.86%、1.25%、1.43%，P-Stribeck模型预测3种缸径液压缸摩擦力NRMSE分别为2.80%、1.55%、0.86%，P-Stribeck模型预测3种密封形式液压缸摩擦力NRMSE分别为0.86%、0.27%、0.46%，P-Stribeck模型预测液压缸稳态摩擦力的精度明显优于Stribeck模型。

(4)采用GMS和P-GMS两种模型预测动态摩擦力，并与实验数据进行对比，结果表明，P-GMS模型预测3种加速度工况下液压缸摩擦力NRMSE分别为3.34%、2.89%、3.23%，P-GMS模型预测3种频率工况下液压缸摩擦力NRMSE分别为7.37%、7.71%、10.92%，P-GMS模型预测液压缸动态摩擦力的精度优于GMS摩擦模型。