2-PUR-PSR并联机构尺度综合多目标优化
2020-11-25张伟中李金平
张伟中 李金平 叶 敏 杨 超
(1.浙江理工大学机械与自动控制学院, 杭州 310018; 2.浙江机电职业技术学院自动化学院, 杭州 310058;3.新南威尔士大学土木与环境工程学院, 悉尼 NSW 2052; 4.长安大学工程机械学院, 西安 710064;5.嘉兴学院机电工程学院, 嘉兴 314001)
0 引言
少自由度并联机构具有结构简单、高承载能力、高刚度、高精度以及优异的运动/力传递性能和动态性能等优势,有效地弥补了串联机构的不足[1-3]。其中,三自由度两转一移(Two rotations and one translations,2R1T)并联机构已广泛应用于诸多领域,如Z3主轴头[4]、Exechon机器人[5-6]、Tricept并联机床[7]和振动筛[8]等。
尽管2R1T并联机构得到了广泛的应用研究,但该类机构的优化设计问题仍未得到很好的解决。运动学性能评价指标和参数优化算法是机构运动学优化设计的主要内容[9-11]。
由于并联机构工作空间相对较小,机构性能优化设计首先需考虑通过优化设计变量获得更大的规则工作空间[12-15]。MASORY等[16]在考虑关节转角约束、杆长约束及杆件干涉的基础上,采用数值积分方法得到了较为接近实际的机构工作空间。CARBONE等[17]采用二进制表达方法得到了可达工作空间体积的数值表达式。RAMANA等[18]采用极坐标方法得到了规则工作空间的最大内切圆柱体积的表达式。BOUNAB[19]计算了Delta并联机构的规则圆球工作空间体积。以上研究将可达工作空间或圆柱、圆球作为规则空间,没有考虑不同高度下的工作空间最大化。
性能分析是并联机构进行尺度综合的前提,而构建合理的运动学指标是并联机构运动学性能分析的重要基础。GOSSELIN等[20]以雅可比矩阵条件数作为机构的性能评价指标。陈修龙等[21]以雅可比矩阵的奇异值作为性能指标,对并联机器人进行结构优化设计。对于混自由度并联机构(包含移动和转动),雅可比矩阵中的元素量纲并不统一,直接计算上述指标会导致机构性能物理意义上的模糊和解释错误。LIU等[22-23]提出了运动/力性能传递指标,该指标具有量纲统一、与坐标系无关、可判断机构的奇异位置等优点,该运动学指标在很多机构分析中得到应用。
尺度综合是以性能指标为衡量标准对机构的尺寸参数进行优化设计,目前主要借助空间模型法对机构进行尺度综合[24]。在工程应用中,往往需要借助智能优化算法对并联机构进行多目标优化,以达到多个目标的综合最优。ZHANG等[25]使用差分进化算法使3-UPU并联机构的刚度和可达工作空间最大化。崔国华等[26]基于Isight优化了3-UPS-S并联机构的工作空间、灵巧度、承载能力和刚度。孙小勇等[27]通过优化数学模型对6-PSS并联机构的工作空间和动力学性能进行了多目标优化。ZHANG等[28]使用遗传算法对球形机构的全局条件数和工作空间进行了多目标优化。
本文以2-PUR-PSR并联机构为例,对其进行结构参数的优化设计,在运动学模型分析基础上,结合螺旋理论,以规则圆台工作空间和全局运动/力传递性能为目标函数,以关节转角和驱动限制为约束条件,采用多目标粒子群优化算法进行尺度综合多目标优化设计,得到满足工作条件的机构规则工作空间和运动/力传递性能的Pareto最优,为得到性能更优的机构提供设计依据。
1 机构描述与运动学分析
1.1 机构描述
如图1所示,由机架、动平台、两条结构完全相同的PUR分支和一条PSR分支组成了2-PUR-PSR并联机构。该机构是为了减小由内副驱动的2-UPR-SPR并联机构在操作过程中的运动质量,并提高机构的刚度进行构型综合,提出的一种由外副驱动的两转一移并联机构[29-30]。机构由固接于机架导轨上的线性驱动器驱动[31-32]。
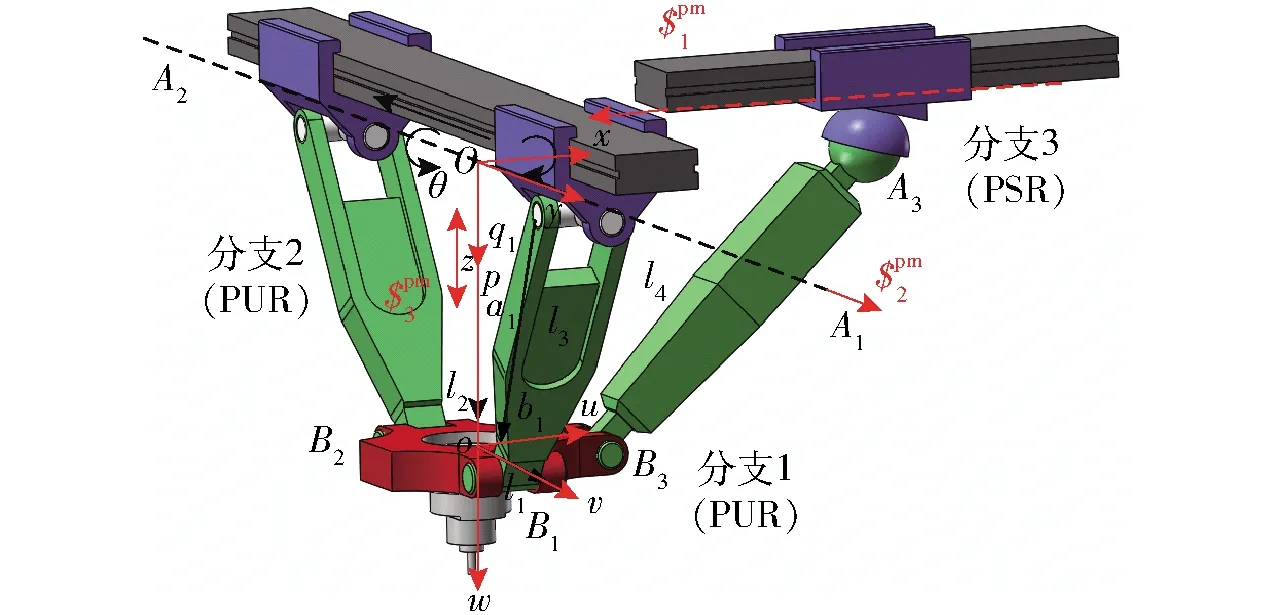
图1 2-PUR-PSR并联机构Fig.1 2-PUR-PSR parallel manipulator
通过驱动P副,3条分支结构与机架的导轨相连。在2条PUR分支结构中,U副的第1个转轴共线,且与其P副的移动方向一致;U副的第2个转轴则垂直于P副的移动方向,同时平行于另一端和动平台相连接的R副轴线方向;并且PUR分支的两个R铰轴线互相平行。S铰是PSR分支与基座相连的点,并与动平台相连的R铰轴线与B1B2平行。其中:Ai表示分支i(i=1, 2, 3)中与基座相邻运动副的中心,A1、A2、A33个点在同一水平面内。分支1、2中虎克铰中心用B1、B2表示;分支3中与动平台相邻的转动副中心用B3表示。
2-PUR-PSR并联机构定/动坐标系原点为A1A2中点,x轴指向A2点,y轴指向A3点,z轴遵循右手法则,从而建立固定坐标系Oxyz。与此同时,以B1点为原点,指向B2点为u轴,垂直于u轴且位于面B1B2B3内为v轴,w轴遵循右手法则,从而在动平台上建立局部坐标系puvw。以A1A2的中心点O为原点,与OA3共线为x轴,沿着OA1方向为y轴,由右手螺旋法则确定z轴,建立定坐标系Oxyz。以B1B2的中心点为原点,与oB3重合为u轴,指向点B1为v轴,由右手法则确定w轴,建立动坐标系ouvw。
对2-PUR-PSR并联机构的结构参数定义为:oB1=oB2=l1,oB3=l2,A1B1=A2B2=l3,A3B3=l4,并且为减少尺寸参数的个数,假定满足l1l4=l2l3。采用文献[33-34]提出的螺旋理论对机构进行分析,可求得2-PUR-PSR并联机构为三自由度机构,分别是2个转动和1个移动自由度。
1.2 位置逆解
已知2-PUR-PSR机构末端点o的位置矢量为p=(x,y,z)T,求解驱动P副的移动距离即为机构的位置逆解问题。
由图1可知,在2-PUR-PSR并联机构中,动坐标系ouvw相对于定坐标系Oxyz的姿态可表示为
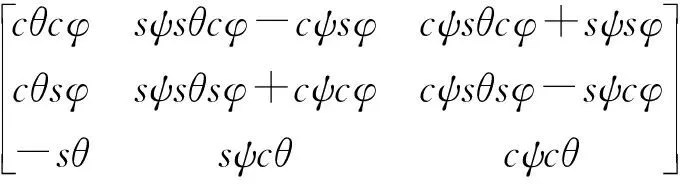
(1)
式中Rz(φ)、Ry(θ)、Rx(ψ)——绕z轴、y轴、x轴的旋转矩阵
c表示余弦函数,s表示正弦函数。
根据图1可得,闭环矢量方程为
qi=p+bi-ai(i=1,2,3)
(2)
式中,分支i驱动器的位置矢量为qi;从点Ai到Bi和从点o到Bi的位置矢量,分别表示为ai和bi,且bi=Rbio,oBi位置矢量在动坐标系{o}下表示为
(3)
同时,ci=Rcio是分支i中R铰轴线的方向矢量,cio为ci在动坐标系ouvw中的方向矢量,表示为
(4)
机构分析可知,机构在运动过程中,各分支的R副轴线始终与qi-p垂直,因此可得
(5)
展开可得各分支的约束关系
xcθcφ-(q1-y)cθsφ-zsθ=0
(6)
xcθcφ+(q2+y)cθsφ-zsθ=0
(7)
y(cψcφ+sψsθsφ)+(q3-x)(cψsφ-sψsθcφ)
(8)
式(6)、(7)相减可得
(q1+q2)cθsφ=0
(9)
在运动过程中,q1+q2不可能恒等于0,为此
cθsφ=0
(10)
式(10)代入式(6)中,可得
xcθcφ-zsθ=0
(11)
由式(11)可得,假定cθ=0,则恒有z=0,这不符合机构的实际运动情况,故sφ=0,φ=0或φ=π。根据2-PUR-PSR并联机构的结构特征,φ不可能等于π,因此φ恒为0。将该结果代入式(8)中,可得
ycψ-(q3-x)sψsθ+zsψcθ=0
(12)
综合式(11)、(12),位置矢量p=(x,y,z)T中的x和y可表示为
(13)
将式(13)代入式(2)中,得到2-PUR-PSR并联机构的位置逆解为
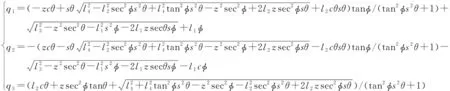
(14)
2 规则工作空间指标
规则工作空间是并联机构的一个重要指标,可以作为优化目标函数之一。在研究规则工作空间之前有必要先对机构的可达工作空间进行研究。并联机构的可达工作空间是指在物理约束下机器人至少从一个方向可以达到的所有点的集合。影响并联机构工作空间的主要因素包括机构的结构尺寸、铰链的转角范围、驱动的限制以及各支链之间的干涉等。
采用极坐标的方法计算2-PUR-PSR并联机构的规则圆台工作空间体积[19]。首先,利用空间搜索法得到可达工作空间的形状,为下一步计算规则工作空间做准备。其次,将操作平台高度划分为n层。最终,计算每一个操作平台高度下可达空间的最大内切圆半径。得到了每一层的最大内切圆半径后便计算规则圆台的工作空间体积,计算公式为
(15)
式中Ai——第i层最大内切圆的面积
Δz——层间的高度间隔区间
给定2-PUR-PSR并联机构的物理约束为
(16)
式中,qmin=50 mm和qmax=800 mm分别为驱动的最小和最大限制,αi1和αi2分别表示第i分支的R铰和U铰的转角,其可以通过运动学分析得到
(17)

图2 2-PUR-PSR并联机构工作空间Fig.2 Workspaces of 2-PUR-PSR parallel manipulator
式中,nli、npi、nbi表示杆件、动平台法线和定平台法线的单位矢量。2-PUR-PSR并联机构在优化前的初始机构参数为l1=l2=200 mm,l3=l4=400 mm。本文采用空间搜索法给出机构的可达离散工作空间如图2所示,可达工作空间关于γ=0°对称,与2-PUR-PSR并联机构的结构吻合。可达工作空间的形状和尺寸不规则,不利于轨迹的规划和算法控制。实际工程应用中一般采用规则工作空间,不失一般性,本文采用每一给定操作平台高度下可达空间的最大内切圆构成的圆台作为机构的规则工作空间,如图2所示,为了确保末端执行器的姿态要求,此处将内切圆的最小半径设置为10°。
3 运动/力传递性能
3.1 局部传递指标
并联机构的本质作用之一是在机构的输入端和输出端之间传递运动和力。研究者据此特性,定义相应的能够同时体现运动和力的传递能力的指标,用以分析并联机构的运动/力传递特性[35-36]。
陈祥等[37]根据力传递性能与传动角的密切关系,提出利用运动/力传递指标(LTI)作为运动学性能评价指标,利用该指标表示机构从输入到输出的传递效率。LTI指标可表示为
(18)
(19)
式中λi——分支i的输入传递指标(ITI)
ηi——输出传递指标(OTI)
$Ai——分支i的输入运动螺旋(ITS)
$Oi——分支i的输出运动螺旋(OTS)
$Ti——分支i的传递力螺旋(TWS)
从式(18)、(19)中可知λi和ηi的取值范围均为0~1;同时值越接近于1,机构的运动/力传递性能越好。对ITI和OTI综合考虑,局部运动/力传递指标(LTI)可以表达为
LTI=min{λi,ηi}
(20)
从式(20)可以看出,LTI计算值的范围为0~1,是一个与坐标系无关的无量纲指标,其值越接近1,表示能量从机构输入端到输出端的传递效率越高。
如图1所示,以机构分支1为例,其运动螺旋系和约束螺旋表达式为
(21)
(22)
由于机构分支1的驱动关节为P副,为此$A1=$11。传递力螺旋$T1与机构分支1中被动关节的互易积为零,即
$T1∘$1i=0 (i=2,3,4)
(23)
通过式(21)、(23)可计算得传递力螺旋$T1表达式为
$T1=(a1/|a1|;q1×a1/|a1|)
(24)
式中 $T1——过点A1、沿a1方向的力螺旋
同理,其余2个分支的传递力螺旋分别为
$T2=(a2/|a2|;q2×a2/|a2|)
(25)
$T3=(a3/|a3|;q3×a3/|a3|)
(26)
式中 $T2——过点A2、沿a2方向的力螺旋
$T3——过点A3、沿a3方向的力螺旋
锁住机构除分支1之外的所有驱动关节,机构分支2和3中的传递力螺旋转变成约束螺旋,机构的约束螺旋系为U1=[$C1$C2$C3$T2$T3],其维度为5,此时机构为单自由度机构,动平台的瞬时运动可通过输出运动螺旋表示为
$O1∘U1=0
(27)
式中 $O1——过点A3且沿A2A3方向的运动螺旋
由式(27)可得输出运动螺旋的表达式为
$O1=
((q3-q2)/|q3-q2|;q2×(q3-q2)/|q3-q2|)
(28)
同理,其余两种情况的输出运动螺旋也可通过该方法得到,分别表示为过点A3且沿A1A3方向和过点A1且沿A1A2方向的运动螺旋。
3.2 全域传递指标
由于LTI指标仅能判断机构在单个位形下的运动/力传递性能,而机构往往在一个特定的工作空间内运行,需要在一个工作空间内去评价机构的运动/力传递性能。为此,定义全局传递指标(GTI)去评价机构在全域的运动学性能指标,表达式为
(29)
在实际计算过程中,采用离散点的数值方法计算GTI,表达式为
(30)
式中n——规则工作空间的离散点的数量
GTI指标越高,意味着机构的运动学性能越好。
4 多目标优化
多目标优化是指同时优化彼此互相冲突的多个目标函数,多目标优化问题的解不唯一,而是一组均衡解,称为非劣解集或Pareto最优解集,且这组解无差别。它是由任一个目标函数值的提高都必须以牺牲其他目标函数值为代价的解组成的。所谓非劣解是指由这样一些解组成的集合(又称非劣解集):与集合之外的任何解相比它们至少有一个目标函数比集合之外的解优,而其他目标函数又不比集合之外的解差。本文以第2节和第3节构建的规则圆台工作空间和GTI作为目标函数,为了将目标函数值控制在同一个量级,将工作空间的体积乘以系数10-3,多目标优化的数学模型为
(31)
其中xdmin=(150, 150, 350)mm
xdmax=(250, 250, 450)mm
式中xd——设计参数矢量
为了求解式(31)的多目标优化问题,采用多目标粒子群(MPSO)优化算法,粒子群(PSO)算法的基本思想是模拟鸟群的觅食行为,群体中每一个体被看作一个在D维搜索空间中没有体积和质量的“粒子”,空间的维数D即为自变量的个数。每一个粒子通过跟踪两个极值来更新自身的空间位置和飞行速度,其中一个极值为单个粒子在自身迭代过程中的最优解粒子,称为个体极值;另一个极值为种群在迭代过程中的最优解粒子,称为全局极值。迭代的过程中粒子会根据自身经验(个体极值)和种群交流(全局极值)来调整搜寻方向和速度,直至找到全局最优解。粒子群算法根据自己的速度决定搜索,替代了遗传算法复杂的交叉和变异操作,具有收敛速度快的优点。
假设种群由N个粒子组成,在D维搜索空间进行搜索,第i个粒子的个体最优位置记为pi=(pi1,pi2,…,piD)(i=1,2,…,N),全局最优位置记为pg=(pg1,pg2,…,pgD),粒子根据这两个最优值更新自己的速度和位置,即
vij(t+1)=ωvij(t)+c1r1(t)(pij(t)-xij(t))+
c2r2(t)(pgi(t)-xij(t))
(32)
xij(t+1)=xij(t)+vij(t+1)
(33)
式中ω——动态惯性权重
c1、c2——学习因子,表示粒子跟踪自己历史最优值和全局最优值的权重
r1、r2——分布于[0,1]区间的随机数
式(32)的第1部分表示粒子之前的速度,用于保证算法的全局收敛性,第2、3部分保证算法具有局部收敛的能力。采用的粒子群优化算法参数设置如表1所示。
图3给出了多目标优化的Pareto前沿,左下角区域的解属于被支配解,右上角区域的解属于不可达到的解。由图可以看出,由于多目标之间的竞争和耦合关系Pareto前沿并不是光滑的曲线分布。图中运动学/力传递性能GTI与Vr成反比,GTI越大,Vr越小。说明GTI与Vr关于结构的几何参数存在竞争关系,无法在Pareto前沿上得到运动学性能与工作空间体积均取得最优的情况,设计人员需要根据两者的权重在Pareto前沿上得到两者的均衡点,从而减少了设计时间。

表1 粒子群优化算法的参数设置Tab.1 Parameter setting of particle swarm optimization algorithm
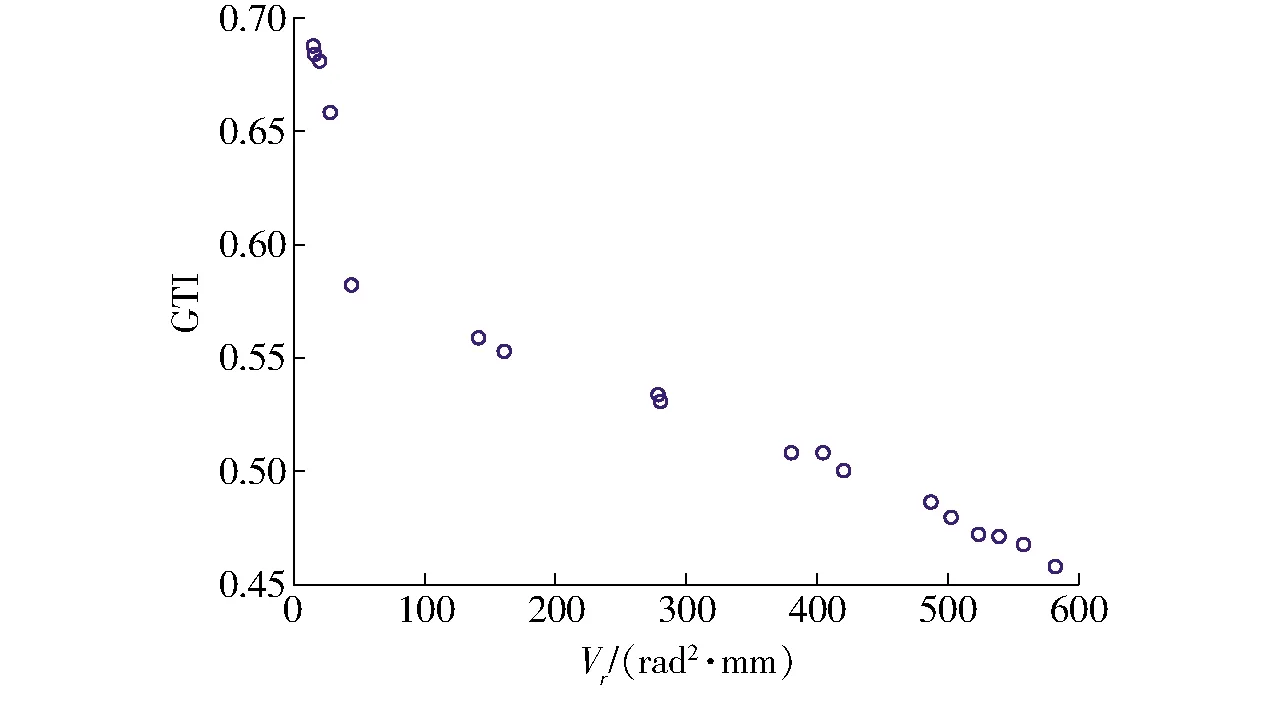
图3 目标函数Vr和GTI的Pareto前沿Fig.3 Pareto front of objective functions Vr and GTI
表2给出了Pareto前沿的18组最优解集以及优化前的机构参数及目标函数值。第1组对应的设计参数(151.92,150.50,402.17)mm对应的工作空间的体积达到了极值582 rad2·mm,比优化前提高了37.59%,GTI却只有0.458;第2组设计参数(169.60,219.09,449.09)mm对应的GTI达到了极大值0.687,比优化前提高了57.57%,但缩小了工作空间的体积。也就是说2-PUR-PSR并联机构的运动学性能与工作空间之间存在着竞争关系,不能同时达到两者的最优,需要工程人员根据需要在两者之间做出取舍。
不失一般性,图4给出了优化后的第2组设计参数在平面z=0.25 m中的LTI指标分布图,可以看出指标关于ψ=0对称,这与机构的对称性是吻合的。图中还可以看出,LTI的最大值不是在初始位置(ψ,θ)=(0°,0°)处而是发生在(γ,β)=(0°,10°)附近的位置。
基于参数优化结果,并考虑加工与装配工艺性,选取其中1组结构参数尺寸,给出该2-PUR-PSR并联机构的设计方案,绘制三维模型图,加工制作样机如图5所示,该机构驱动器均设置在装置的机架上,机构运动时电机不会跟随机构杆件一同运动,从而减轻了机构运动质量,进而减轻了装置的负荷,提高了装置的驱动能力。因此,这种机构具有较好的运动稳定性、实时控制性强等优点。
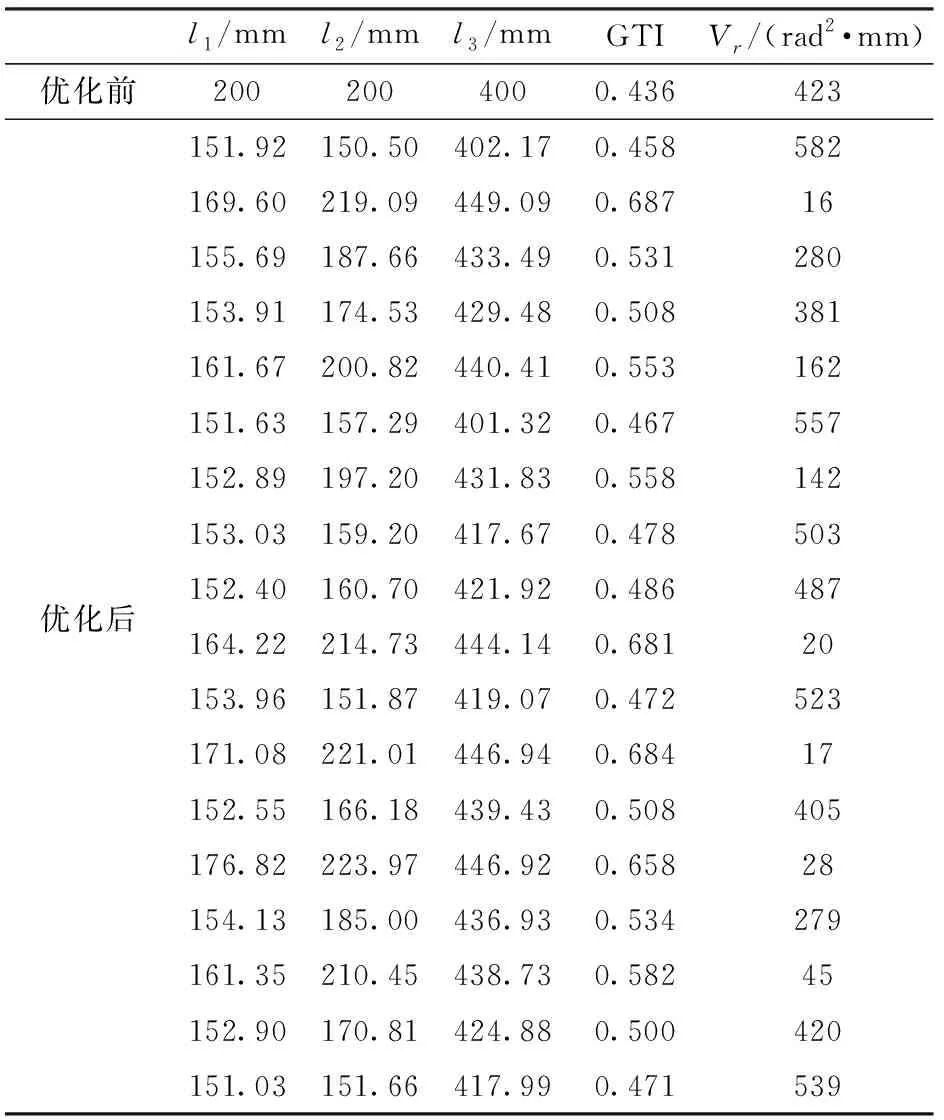
表2 Pareto前沿的最优解集以及优化前的机构参数及目标函数值Tab.2 Optimal solutions and optimization of Pareto frontier and previous mechanism parameters and objective function values
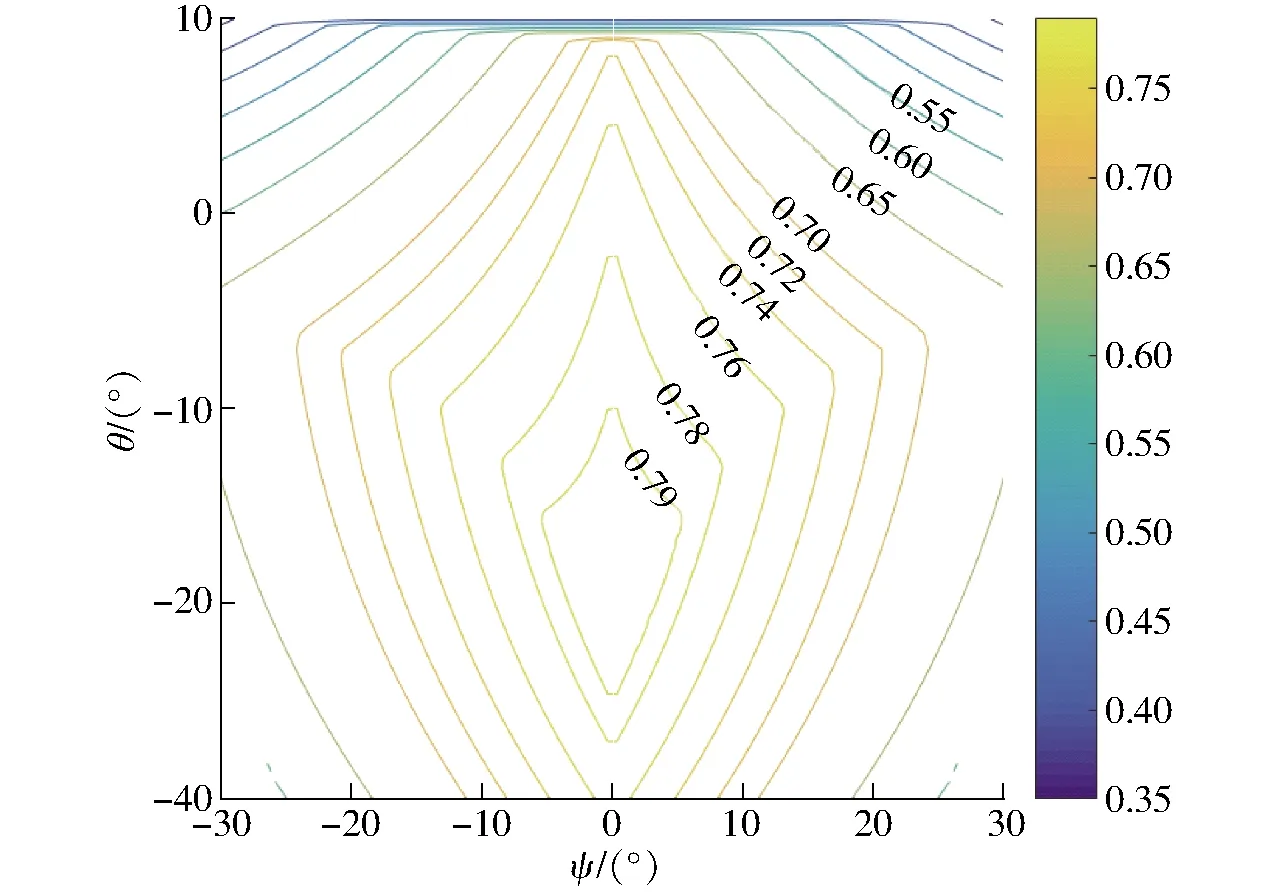
图4 2-PUR-PSR并联机构LTI在平面z=0.25 m内的LTI分布图Fig.4 Distribution of LTI of 2-PUR-PSR parallel manipulator in plane z=0.25 m

图5 2-PUR-PSR样机Fig.5 Prototype of 2-PUR-PSR1.分支1(PUR) 2.驱动电机 3.分支2(PUR) 4.动平台 5.分支3(PSR)
5 结论
(1)提出了基于极坐标方法的规则圆台工作空间体积的计算方法,以2-PUR-PSR为研究对象,以规则工作圆台空间体积和GTI为目标函数,以驱动限制和关节转角限制为约束条件,以机构参数为设计变量,建立了2-PUR-PSR并联机构尺度综合多目标优化数学模型。
(2)基于MPSO算法得到了2-PUR-PSR并联机构尺度综合多目标优化的Pareto前沿,给出了18组Pareto最优解集,节约了设计时间。Pareto前沿的GTI最优值比优化前提高了57.57%,Vr最优值比优化前提高了37.59%,证明了优化方法的有效性。
(3)建立的2-PUR-PSR并联机构的尺度综合多目标优化模型也同样适用于其他同类型的并联机构。以机构在给定工作空间内具有优良的运动/力传递性能为目标,实现其尺度参数优选,可为后续机构刚度、运动学误差、动力学等性能分析以及样机制造奠定基础。
