某重型变速器壳体的结构动力学优化
2020-11-23杨啟梁李瑾宁
杨啟梁,任 波,李瑾宁,胡 溧
(1.武汉科技大学汽车与交通工程学院,湖北 武汉 430081;2.东风商用车有限公司技术中心,湖北 武汉 430056)
1 引言
结构动力学优化,是指若原结构动态特性不符合要求,如何修改物理参数及确定修改量,使其动态特性满足给定的要求[1]。建立一个精确的结构有限元模型是解决结构动力学优化问题的关键[2]。有限元模型修正一般基于计算模态分析技术和试验模态分析技术[3]。主要分为矩阵参数修正法和模型参数修正法[4-5]。矩阵型修正方法即对模型的质量矩阵和刚度矩阵进行修改,工程实际中矩阵型参数修正实施起来难度很大。一般采用模型参数修正,即采用结构优化的思想,以结构物理参数为优化变量进行优化,该方法适用于复杂结构的有限元模型修正。结构动力学优化研究的对象多为板壳结构,如车门[6],白车身[7],车架[8]等,设计变量多为结构厚度。在变速箱相关研究领域,多以整体式轻型变速箱壳体为研究对象,较少涉及重型变速器。多以单元密度为设计变量,采用拓扑优化法来改善其动态特性[9-10],采用结构动力学优化法相对较小。拓扑优化对结构设计初期阶段具有一定的指导意义,但在设计后期,当结构造型已经确定,无法做较大改动,此时该方法计将无法很好的达成设计要求,结构动力学优化则能很好的完成设计目标。
研究对象为复杂的分段式重型变速器壳体,在已对模型进行结构误差和模型阶次误差修正的基础上,基于LMS.Test.Lab 的试验模态分析及Hypermesh 计算模态分析结果,运用Hyperstudy 软件,采用模型参数修正法对壳体有限元模型进行修正,进一步提高了模型的精度。与大多数板壳及规则的实体结构不同,无法将该变速器壳体厚度作为变量进行优化。因此提出,基于Creo 及Workbench 软件,以优化壳体加强筋相关参数的方式对其进行结构动力学优化,以此来改善变速器壳体的动态特性。
2 模态分析
2.1 试验模态分析
试验对象为某重型商用车变速器壳体。试验目的为测得变速器壳体自由模态的固有频率与振型。由于重型变速器壳体质量较大,不便于悬挂,因此将试件放在弹性轮胎上来进行自由边界条件的模拟。使用LMS.Testlab 软件中MIMO FRF Testing 模块进行试验模态分析。壳体被离散成171 个测点,激励信号采用猝发随机,选择82 号测点为激励点。测试带宽根据试验目选定为2048Hz,频率分辨率为1Hz。5 个测点采集一组数据,同步采集测点3 个方向的振动响应,平均30 次采样数据得到各测点频率响应数据。变速器壳体测点模型,如图1 所示。采集完全部测点的频率响应数据后,基于“最小二乘复频域法(LSCF)”对该壳体的模态参数如固有频率及振型进行识别,获取了表征壳体模态参数的稳态图,如图2 所示。

图1 试验模态测点模型Fig.1 Measuring Point of Free Experimental Modal

图2 自由模态测试稳态图Fig.2 Stabilization Diagram of Free Experimental Modal
2.2 计算模态分析
基于Hypermesh 有限元分析软件,使用Block Lanczos 法来提取变速器壳体自由模态的模态参数。变速箱壳体初始材料属性为HT250,弹性模量为130GPa,泊松比为0.25,密度为 7350kg/m3。该壳体的有限元模型未进行大幅度简化,避免了结构参数误差。主箱的网格单元阶次可设为一阶单元(Hypermesh 默认单元阶次)和二阶单元,主副箱箱体间的螺栓连接属性可以采用刚性单元连接(RBE2)及面面接触(Contact)进行模拟。通过比较发现,采用二阶四面体单元对变速器壳体模型进行网格划分及主副箱箱体间的连接采用优于螺栓连接(RBE2)的面面接触,能够得到更准确的模态参数。
3 壳体有限元模型修正
采用结构优化设计的思想,基于Hyperstudy 有限元分析软件,从壳体的材料属性入手,对该壳体模型进行修正。结构优化设计一般由设计变量,约束函数,目标函数三个要素组成。本次有限元模型修正,设计变量为壳体材料的弹性模量、泊松比和密度,如式(1)所示。设计变量初始值及上下边界,如表1 所示。约束函数为各阶试验模态和计算模态固有频率相对误差的绝对值,要求该误差值限定在4%以内,如式(2)所示。目标函数为全部6 阶模态固有频率绝对误差的平方和,如式(3)所示。要求该目标函数在上述约束条件下,取得最小值。

Hyperstudy 软件中集成了多种优化算法,如自适应响应面法、可行方向法,及遗传算法等。本次模型修正采用自适应响应面法,该方法多用来解决非线性问题且迭代收敛速度较快[11]。经过9次迭代后的最终材料参数,如表1 所示。使用优化后的材料参数进行自由模态计算的最终结果,如表2 所示。修正前后壳体前6阶自由模态固有频率对比,如表2 所示。分析表2 可知,自由模态固有频率的最高值由4.7%降到了3.6%,第1、4、5、6 阶误差也有显著下降,仅2、3 两阶误差有部分提高。因此,结构优化法可用来修正有限元模型,并使得模型的计算精度有较大的提高。上述模型修正,使得该壳体的固有振动特性得到更加真实地反映,为进一步研究其动力学特性提供了更加准确的模型基础。
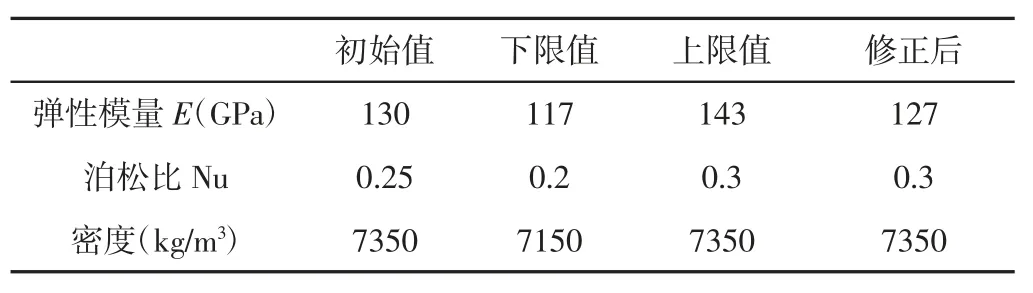
表1 设计变量相关参数Tab.1 Related Parameters of Design Variables
4 壳体结构动力学优化
基于Workbench 软件,对修正后的变速箱壳体模型进行约束模态分析,约束前副箱端面的全部自由度。最终得到该变速箱壳体的前10 阶约束模态固有频率及振型,前10 阶固有频率,如表4 所示。第8 第9 阶振型,如图3 所示。
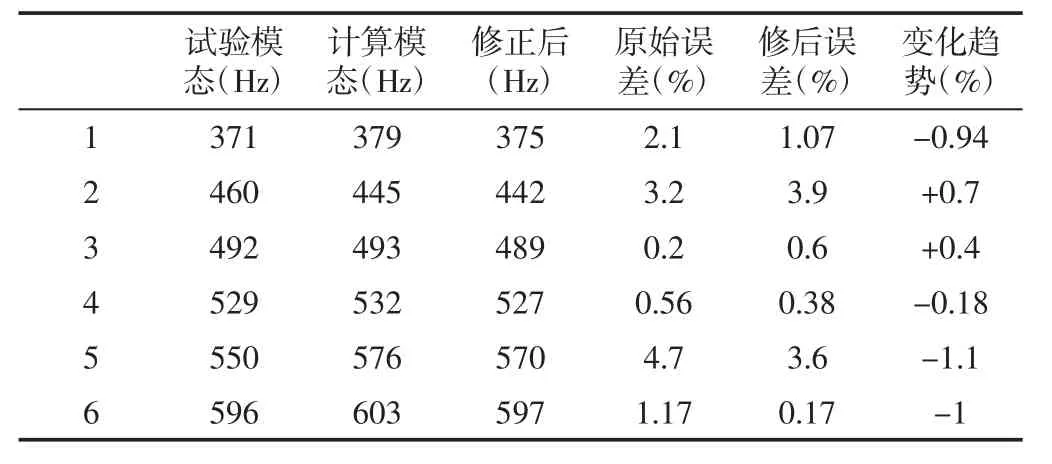
表2 修正前后自由模态固有频率对比Tab.2 Natural Frequency Contrast of Free Model Before and After Correction

图3 约束模态第8 及第9 阶振型Fig.3 Constraint Computational Modes of 8th and 9th Order
研究发现,匹配该变速箱的车型,在良好的路面上,在常用转速为1500RPM 下,13 档低半档齿轮副啮合频率(650Hz)与壳体第9 阶固有频率(647Hz)相近,因此在该转速下,该档位齿轮副的啮合激励会导致变速箱壳体产生共振。此外第8 阶固有频率(640Hz)也应重点关注。为了改善该变速箱的NVH 性能,避免该工况下发生壳体共振,因此需要对壳体进行结构动力学优化,以此来优化其结构的动态特性并指导工程实际运用。
4.1 参数关联性分析
观察壳体第8 及第9 阶约束模态振型可知,大变形发生在该变速器壳体主箱部位,通过Creo4.0 软件对该变速器壳体的主箱有限元模型外表面上的加强筋进行参数化处理,将筋的厚度与高度尺寸作为优化参数,最终导入到Workbench 软件进行结构动力学优化,以此来改善变速箱的NVH 性能。
主箱外表面共有13 条加强筋,分别编号(1~13),厚度参数标识符“DS_W”,高度参数标识符为“DS_H”,共计26 个输入参数。该壳体有限元模型网格及节点数量较大,参数较多,单次计算时间过长,此外后续动力学优化需要使用灵敏度数据,因此,采用Workben 中“参数关联性分析”得到输入对输出参数的灵敏度,通过参数灵敏度来确定影响输出参数的主要的输入参数,并以主要输入参数作为输入进行结构动力学优化,以此来减少参数数量及计算规模。由于箱体加强筋的制造工艺—高度要求一致,因此不对加强筋高度做灵敏度分析,仅对其厚度进行参数相关分析,输入参数为13 条加强筋的厚度,输出参数为该壳体第8 和第9 阶约束模态固有频率,其中加强筋的初始厚度等于主箱壁厚8mm。

图4 加强筋厚度对第8 及第9 阶固有频率的灵敏度Fig.4 The Sensitivity of Ribs Thickness to Natural Frequencies of 8th and 9th Order
关联性分析方法为Speraman(斯皮尔曼等级相关系数,多用于非线性的参数关系),设计点样本数为100 组,参数上下限依据初始值由软件自动生成,最终得到各筋的厚度对第8 和第9 阶固有频率的灵敏度,如图4 所示。W01,DS_W02,DS_W10,主要影响壳体第9 阶固有频率的参数为DS_W02,DS_W04,DS_W05,DS_W09,即 1 号筋、2 号筋、4 号筋、5 号筋、9 号筋和10 号筋的厚度为影响第8 和第9 阶固有频率的主要输入参数。
4.2 结构动力学优化
结构动力学优化的三要素为输入参数,约束函数及目标函数。本次优化输入参数为加强筋的厚度与高度;约束函数为第8阶模态固有频率小于等于642Hz(要求第8 阶固有频率变化幅度较小);第9 阶固有频率大于653Hz;目标函数为在该输入参数和约束条件下,求得第9 阶固有频率的最大值。在优化过程中,为了使得第8 阶频率变化较小,因此对该阶频率较灵敏的参数应当舍去,主要以第9 阶灵敏度参数作为输入。结合图4 中灵敏度数据,去掉 DS_W02,选择 DS_W04,DS_W05,DS_W09 为厚度优化参数。由于加强筋的制造工艺要求其高度必须一致,因此,将1 号加强筋(1~13 号任意加强筋都可以)的高度设为主动输入参数,2 到13 号筋的高度设为驱动输入参数,即2 到13 号筋的高度值由1号筋进行驱动并赋予相同的值。因此优化的输入参数为:DS_W04,DS_W05,DS_W09,DS_H01。参考强筋制造工艺相关要求,筋的厚度小于等于所在壁厚,筋的高度小于3 到5 倍的壁厚,筋的高度太大,会导致加强筋的开裂失效,因此加强筋的厚度优化区间为(4~8)mm,加强筋的高度优化区间为(8~16)mm,如表 3所示。本次优化采用“单目标自适应优化算法(Adaptive Single-Objective)”,最终输入参数优化结果,如表3 所示。将优化后的参数赋于模型,其它的尺寸保持原尺寸不变,最终优化后壳体的约束模态固有频率,如表4 所示。
分析表4 可知,经过动力学优化后:(1)第9 阶模态固有频率由初始的647Hz 提高至662Hz,避开了低半档齿轮副啮合频率650Hz;(2)第 8 阶固有频率由 640Hz 提高至 642Hz,该值变化较小,满足优化要求。综上该壳体结构动力学优化达成目标。
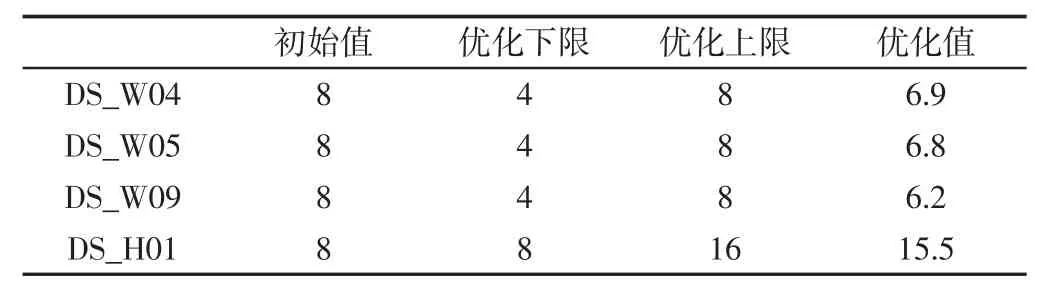
表3 结构动力学优化相关参数(单位:mm)Tab.3 Related Parameters of Structural Optimization(Unit:mm)

表4 优化前后约束模态前10 阶固有频率(单位:Hz)Tab.4 The First 10 Natural Frequencies of Constrained Model Before and After Optimization(Unit:Hz)
5 结语
针对重型变速器壳体有限元模型进行了修正并对修正后的有限元模型进行了结构动力学优化,该分析思路及方法可为类似结构动力学优化问题提供参考,分析结果可以指导工程实际应用。主要结论如下:
(1)对于类似变速箱壳体的装配体进行模态分析时,应当注意结构的有限元网格的阶次及各部分零件间的连接属性,高阶单元及适当的连接属性可以提高模型的精度;
(2)采用结构优化思想,基于(1)中修正结果,以材料的弹性模量、泊松比及密度为优化设计变量进行模型修正,可以进一步提高模型的精度;
(3)对于结构动力学优化问题,当输入参数较多时,采用“参数关联性分析”得到输入参数对输出参数的灵敏度,可以缩减优化参数数量,提高优化速度;
(4)对于类似该变速箱的实体结构,在进行结构动力学优化问题时,无法像板壳及规则实体结构将厚度作为优化变量参数时,可以考虑将加强筋相关参数作为变量进行优化。
