转盘式间歇运动机构的设计与特性分析

王 源 ，张耀成 ，杨兆建 ，高慧芳

（1.太原理工大学机械工程学院，山西 太原 030024；2.煤矿综采装备山西省重点实验室，山西 太原 030024）

1 引言

间歇运动机构是指有一部分机械需要其机构周期地运动和停歇。它可以将原动件的连续转动转变为从动件周期性运动和停歇的杆件。我们常见的间歇机构有凸轮、棘轮、不完全齿轮、槽轮等等。在很多机械设备中，都有构件呈周期性的间歇运动。例如在牛头刨床工作台的横向进给运动，电影放映机的送片运动，装配线上的步进输送运动等等[1]。他们具有结构简单，价格低廉、工作可靠、且可以承受一定的冲击载荷[2]。

间歇机构的种类和形式多种多样，所产生的设计方法和思路也是各有不同。某科研人员优化设计了槽轮间歇机构，建立其数学模型，并对参数进行了优化，有效解决了槽轮运行的不稳定性。科研人员设计提出了行星分度凸轮机构，其具有结构简单、体积小、分度数大及承载能力大等特点。文献[3]提出了带有椭圆齿轮的行星间歇机构的运动学方案，所设计的机构结构紧凑、可靠，可广泛应用于机床、机器人、自动机械、输送机等领域。文献[4]介绍了一种新型间歇机构，通过这种间歇机构，可以在低冲击下更好展开铰链，最大角速度和冲击力可以减小90%以上。

所研究的转盘式间歇机构的结构与槽轮相似，但是槽轮机构中两个构件的尺寸要基本近似相同，否则就不满足几何约束条件，而且槽轮动停比不能随意变化，所以这些都一定程度上限制了它的使用，而转盘式间歇机构的设计比起槽轮更加灵活自由，对于构件的尺寸要求限制小，这样也会为转盘式间歇机构的使用提供了更加广泛的应用空间。

2 转盘式间歇机构的设计

2.1 基本结构和工作原理

转盘式间歇机构主要包络两个部件，如图1 所示。从动件为转杆，杆数为四杆，并且在四个杆端上各有一个圆销A、B、C、D，转杆可绕着O2旋转。主动件为一个转盘，可绕着O1旋转，其上有多段凹槽弧，可以与转杆的圆销配合起来，凹槽弧的组成主要包括两种：运动弧和静止弧。其中弧EF 为运动弧，弧EPF 为静止弧，除了凹槽弧，转盘上还有槽口M 和槽口N。转盘是一个轴对称图形。

这种转盘式间歇机构的工作原理具体为：首先假设圆A 与圆销B 在静止弧EPF 中，当转盘顺时针绕着圆心O1旋转时，由于静止弧的弧长半径是相同的，此时，转杆的两个圆销都被约束在静止弧中，是不会动作的，接着转盘继续旋转，运动到到圆销A开始接触运动弧EF 的E 处时，由于弧EF 的弧半径与弧EPF 不一样，圆销A 会顺着弧EF 运动，与此相对，圆销B 绕着O2也开始逆时针旋转，通过槽口N 离开，渐渐远离转盘，当圆销A 慢慢到达运动弧的F 处时，圆销D 会通过槽口M 进入转盘，由此圆销A 与圆销D 都进入静止弧中。这样就完成了转盘式间歇机构的一个工作行程。即转盘旋转一圈，而转杆旋转1/4 圈。

图1 转盘间歇机构的基本结构Fig.1 Turntable Intermittent Motion Mechanism

2.2 槽轮凹槽弧的设计

首先明确设计条件，这里设定转杆的杆长长度O2A，转盘和转杆的中心距O1O2，并让运动弧EF 弧度为α。即∠EO1F=α。

第一步，我们对静止弧的弧长和弧度求解，如图1 中，根据余弦公式可知：

由几何条件可知整个静止弧所占弧度为2π-α。

第二步我们对运动弧EF 求解，如图2 是一个特殊位置，此时，转杆由于凹槽弧的带动旋转了1/8 圈，来到了运动弧EF 的中点H，E、F、H 是设计运动弧的三个关键点，其中FH 和HE 关于O1O2对称，我们求解弧FH，弧HE 也可随之确定，为了在F 和H处圆滑过渡而不产生刚性冲击[5]，在弧连接处的斜率要一致，所以我们采用了两段圆弧过渡的方法，分为圆弧FK 与圆弧KH，它们的圆心分别为 O3与 O4，其中 O1与 O3共线，O3与 O4共线，O1与O4共线，这样就分别保证了F、K、H 三点的圆弧连接处的斜率一致，根据余弦定理和勾股定理可知[6]：

得到弧FK 和弧KH 的弧长后，然后再利用余弦公式对弧FK 和弧 KH 的圆心角∠FO3K 和∠KO4H 求解：

以 O1为圆心，O1O2为x 轴，垂直O1O2为y 轴建立直角坐标系，要确立凹槽弧数学表达式还需要知道圆弧FK 与圆弧KH 的在坐标系中所占的弧度即∠FO1K 和∠KO1H。相同弧长下，圆心角与半径成反比。由此可知：

又由几何条件可知：

通过以上的求解，我们就可以确定凹槽弧的弧线方程：

式（8）是凹槽弧 0～π 的方程，另 π～2π 关于 O1O2轴对称。由此我们就确定了整个凹槽弧的数学解析式。

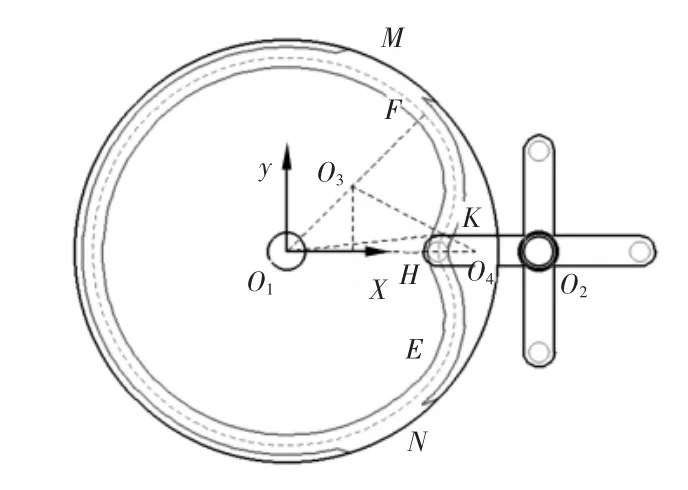
图2 转盘运动弧的求解Fig.2 Solving the Motion Arc of a Turntable

3 转盘式间歇机构的运动特性分析

3.1 模型的建立和约束的添加

采用传统的设计方法，需要制造多个物理样机，设计周期长、成本高，而虚拟样机设计可以很好地简化这一过程。Pro/E 是一款基于特征的全参数化建模软件，目前有80 多个专用模块，功能强大。机构运动仿真是Pro/E 包含运动的一个模块，能够对设计进行模拟仿真校验，如运动仿真显示、运动轨迹、位移、速度、加速度计算等[7]。利用Pro/E 可方便的设计转盘式间歇机构的三维立体模型并进行整体装配，运用其机构运动仿真模块能够进行各零部件的运动分析[8]。通过Pro/E 中建立好转盘和转杆的三维模型后，还需要建立一个缺省件，缺省件的主要作用是固定转盘和转杆的相对位置。随后我们要对三个模型进行装配，先行导入缺省件，并将其设置在缺省的转配模式，接着导入转盘和转杆，这两个部件要使用销钉类型装配到缺省件的轴上，如图3 即为创建的模型，完成后我们要在Pro/E 中的机构模块下进行运动仿真[9]。

图3 三维模型的建立和装配Fig.3 Establishment and Assembly of 3D Model

首先在转盘的安装轴上定义一个伺服电机，并确定好方向和角速度，接着我们要约束转盘的凹槽弧和转杆的圆销的运动。要使用凸轮设置将转杆圆销的曲面和转盘凹槽弧的曲面全部约束上，同时我们要在属性中选择启动升离[10]。这样对于转盘和转杆的运动仿真和和参数设置完成，最后在运动分析窗口的类型下选择运动学，规定好帧数后即可观察转盘式间歇机构的运动，最后将运动动画保存后就可以分析从动件转杆的运动特性。

3.2 间歇机构的运动特性研究

由于转盘式间歇机构的转杆在静止弧是不运动的，所以只对转杆在运动弧下的运动特性进行分析，下面用一个实例来说明，首先设置转杆的杆长O2A=100mm，转盘和转杆的中心距O1O2=180mm，运动弧弧度α=π/2。定义伺服电机的角速度即转盘角速度为5deg/s。其转杆的输出角速度和角加速度，如图4、图5 所示。

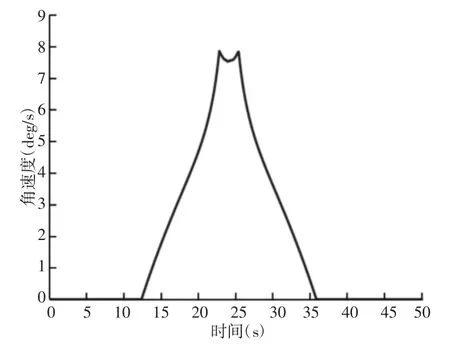
图4 四杆转杆角速度图Fig.4 Angular Velocity Diagram of Four Rod

图5 四杆转杆角加速度图Fig.5 Angular Accelerometer of Four Rod

从图4 和图5 可以看到，角速速最大值为7.8deg/s，角加速度最大值为2.23deg/s2，通过角速度图可以看出其图像是连续的，其最大角速度会在凹槽弧的K 处出现，接着速度有所下降，由于凹槽弧是轴对称图形，后面的变化规律也是对称的。而通过角加速度图像可知，角加速度会在各个圆弧连接处发生突变，可知此时会有一定冲击，不过角加速度的变化值是有限值，说明这是一种柔性冲击，不是刚性冲击，对于部件的损伤是较小的[11]。

3.3 转杆为不同杆数下的特性研究

以上是对转杆的杆数是四杆的研究，现在对不同杆数下的运动特性进行分析，设定的中心距，杆长，转盘角速度和与上文一致。

这里主要是以三杆，四杆和五杆进行比较。三杆与五杆所对应的转盘的凹槽弧会有所变化，但计算过程与四杆是类似的，这里就不在赘述。经过在Pro/E 运动仿真后，三杆和五杆的角速度和加角速度，如图6～图9 所示。并综合了主要的三个参数列出表一进行比较。通过对于不用杆数下角速度和角加速度图像的观察可以发现，虽然杆数不同，但总体曲线的变化趋势是相似的。不论是三杆、四杆或者五杆，存在的冲击只有柔性冲击，再结合表一，我们可知，转杆的杆数越大，相对应的最大角速度也会变小，但变化幅度不是很大，角加速度随着杆数的增加，会有所增大，与角速度变化正好相反。而凹槽弧最大半径即静止弧的半径会随着杆数的增加而减少，而其主要影响的是转盘式间歇机构的尺寸。当在适宜的条件下，由于三杆角加速度较小，可以优先选择杆数为三杆的间歇机构作为工程上的应用。

图6 三杆转杆的角速度图Fig.6 Angular Velocity Diagram of Three Rod

图7 三杆转杆的角加速度图Fig.7 Angular Accelerometer of Three Rod

图8 五杆转杆的角速度图Fig.8 Angular Velocity Diagram of Five Rod

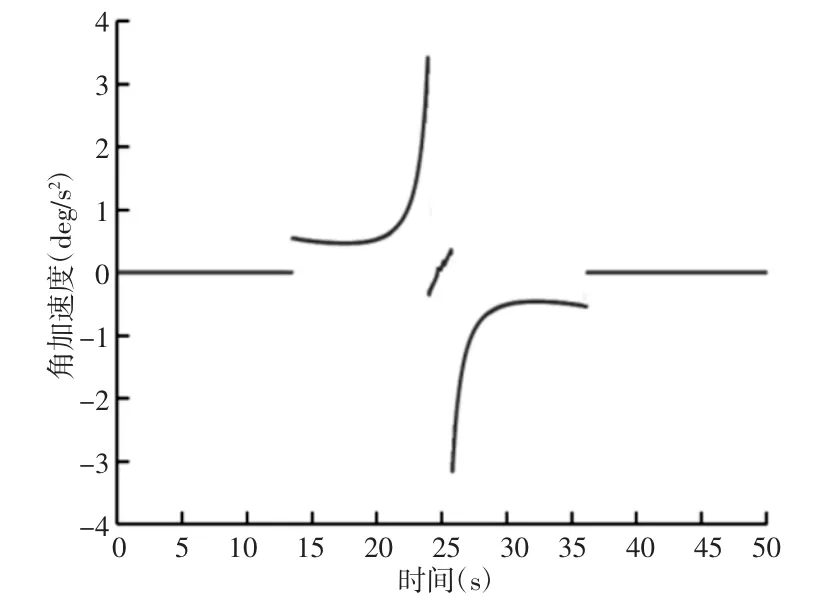
图9 五杆转杆的角加速度图Fig.9 Angular Accelerometer of Five Rod

表1 对于不同杆数下的参数比较Tab.1 Comparison of Parameters Under Different Rod Numbers

3.4 不同运动弧弧度下的运动特性比较

转盘式间歇机构的另一重要个参数是动停比，即转盘运动一圈时，转杆运动的时间与转盘运动时间之比[12]：

通过改变运动弧弧度α 我们就可以改变转盘式的间歇机构的动停比，这相比槽轮的固定的动停比有着极大的优势，通过这种特性，转盘式间歇机构的使用范围也会大大提高。

在这里依然设置转杆的杆长O2A=100mm，转盘和转杆的中心距为O1O2=180mm，转杆杆数为4 杆，转盘角速度为5deg/s，而α 分别为 π/3、π/2、2π/3。然后将其导入 Pro/E 中进行运动仿真，由于其图像和之前图像类似，这里只列出表二进行比较。

表2 对于运动弧弧度下的参数比较Tab.2 Comparison of Parameters Under Arcs of Motion Arc

不同运动弧弧度下的角速度和角加速度图像的变化趋势还是较为相似的。也只存在柔性冲击，而不存在刚性冲击。通过表2可以看出运动弧弧度越大，即动停比越大，角速度和角加速度的最大值也会相应减小，说明了动停比越大，转杆的运动更加平缓。

4 结论

（1）所研究的转盘式间歇机构与槽轮间歇机构相比较具有更大优势，可自由的选择动停比，设计自由度更高，所对应的工程实践范围也会更加广泛。（2）转盘上凹槽弧的数学解析式使用了斜率相同的圆弧进行连接，避免了折线过渡，从而消除了刚性冲击，极大的减少了对于整个机构的损伤，利用Pro/E 三维软件建立了其模型，并在运动仿真模块下论证了转盘式间歇机构是可行的。（3）比较了杆数不同和动停比不同下的运动规律，结果表明三杆和高动停比下的运动特性更加平缓，冲击更小。