量子遗传算法和神经网络的锅炉燃烧优化控制

2020-11-23董胡适蒋国璋段现银

机械设计与制造 2020年11期

董胡适，蒋国璋，段现银

（武汉科技大学机械自动化学院，湖北武汉 430081）

1 引言

目前，节能与环保是世界上极为受到重视的两大主题，随着国家对发电站NO 排放的限制，如何有效降低NO 排放的技术也是发电站当前关注的热点[1]。由于锅炉燃烧优化控制技术可以降低发电成本，并有效提高锅炉燃烧效率和降低锅炉NO 排放，因此研究锅炉燃烧优化控制技术早已是一项重要的研究话题。

针对锅炉燃烧过程是一个多变量、非线性和大滞后等问题，目前一些学者研究报道，文献[2]针对锅炉燃烧系统运行数据建立排气温度模型，提出一种最小二乘支持向量机模型的自适应算法，对锅炉燃烧系统进行自适应实时控制。文献[3]针对锅炉燃烧的输入变量和排烟温度、飞灰的含碳量和NO 排放量，建立基于人工神经网络的直接燃烧优化模型和混合燃烧优化模型，来提高预测精度。文献[4]建立锅炉在线应用燃烧优化框架模型，提出一种改进人工蜂群算法，对锅炉燃烧系统具有较好的在线优化和预测控制。文献[5]针对锅炉燃烧优化中反向传播神经网络泛化能力较差问题，提出一种贝叶斯正则化BP 神经网络和遗传算法的混合算法，优化结果表明该方法较好预测热效率和NOx排放，解决了锅炉燃烧的多目标优化问题。文献[6]建立了锅炉燃烧优化系统，利用神经网络和遗传算法结合的方法，实现燃煤锅炉高效低排放的要求。以上这些方法都具有各自的特色和优点，但是算法收敛速度慢、泛化能力弱，不满足现场对锅炉燃烧快速优化和预测控制的要求。

综上所述，锅炉燃烧优化技术大部分针对燃烧热效率和污染物排放量的优化目标，但由于各自优化方法独特性。研究以燃烧效率和氮氧化物的排放为优化目标，建立发电站锅炉燃烧特性的神经网络模型进行预测，再利用量子遗传算法寻找最佳送风量和燃烧器优化值，来调节风门开度和燃烧器摆度，从而达到锅炉燃烧优化控制目标。仿真实验证明，提出量子遗传算法的神经网络来优化锅炉燃烧控制是一种有效的优化方法。

2 锅炉燃烧控制优化方案设计

2.1 风门开度和燃烧器系统图

为使锅炉燃烧热效率和污染物排放量达到最佳，通过改变风门开度和燃烧器摆角来控制燃烧。以实现炉膛内的燃料充分燃烧，达到锅炉燃烧优化控制的最优燃烧效率[7]。下图为风门开度-燃烧器摆角系统图，如图1 所示。

图1 风门开度-燃烧器摆角系统图Fig.1 Air Door Opening-Burner Angle System

通过改变风门开度和燃烧器摆角来控制燃烧情况，同时也对锅炉炉膛燃烧状况检测，从而进行反馈调整风门开度和燃烧器摆角大小，保证燃烧系统充分燃烧。

2.2 优化方案

采用量子遗传算法（QGA）寻找最佳风门开度和燃烧器摆度的值，从而实现锅炉的高效低污染燃烧。使用量子遗传算法来优化燃烧效率和氮氧排放量，来实现神经网预测。算法优化方案图，如图2 所示。

图2 算法优化方案图Fig.2 Algorithm Optimization Scheme

3 锅炉燃烧系统控制建模

锅炉燃烧过程中伴随着多扰动，变周期、多变量的情况，其系统建模复杂多变，常规方法难以解决复杂模型问题。由于神经网络具有很强的非线性映射能力和良好的泛化能力，因此对锅炉燃烧系统控制采用BP 神经网络来建立模型。

3.1 锅炉燃烧特性与神经网络样本数据

发电站锅炉燃烧系统具有多输入和多输出的特点，燃烧效率和氮氧化物排放与很多影响因素有关，根据燃烧特性试验表1主要影响因素共进行了12 组试验工况[8]，建立锅炉燃烧的神经网络模型，特性试验数据，如表1 所示。

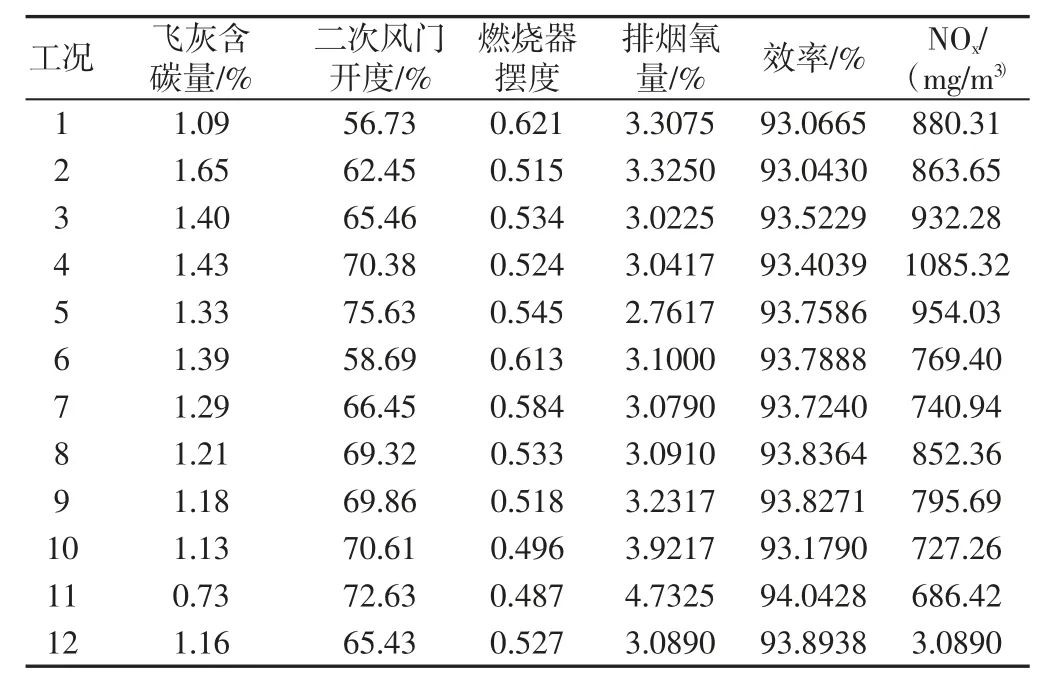
表1 锅炉燃烧特性工况表Tab.1 Boiler Combustion Characteristics

3.2 锅炉燃烧过程神经网络模型

在分析了锅炉燃烧特性的基础上，根据表1 主要影响因素试验数据，本网络模型采用输入层为10 个节点和输出层为2 个结点，一个单隐层的网络结构，建立3 层BP 网络模型，选择燃烧效率和氮氧化物排放10 个因素作为神经网络输入（总风量、燃料量、二次风门开度、燃尽风门开度、风箱炉膛差压、磨煤机通风量、给煤机的开度、燃烧器摆动角、空预器出口温度、燃料成分），神经网络输出为燃烧效率和氮氧排放量[9]，如图3 所示。

图3 基于量子遗传算法的神经网络锅炉燃烧优化模型Fig.3 Neural Network Boiler Combustion Optimization Model Based on Quantum Genetic Algorithm

4 量子遗传算法

4.1 量子比特编码

量子比特是一个双态量子系统，主要作用在量子计算机中充当信息存储单元的物理介质。量子比特不同之处在于，它可以处在两个量子态的叠加态中

式中：（α，β）—两个幅常数。

式中：|0〉—自旋向下态；|1〉—为自旋向上态。因此一个量子比特表示|0〉和|1〉两种态。

在量子遗传算法中，基因表示为量子比特。基因可以是任意叠加态，也可以是0 态或1 态。在此基因表示是一种包含所有有用信息的集合，而不再是一个确定值，而对该基因作出任何操作会作用在所有有用信息上[10]。以染色体的多个态叠加来表达量子比特编码，与经典遗传算法相比，量子遗传算法具有更好的多样性特征，算法的全局搜索性能更强，同时也可以获得较好的收敛性。当量子比特编码上无限趋于0 或1 时，染色体将收敛成为一个单一态，种群的多样性就越不明显。

4.2 量子门更新

量子门是量子遗传算法的演化过程中的关键，先针对问题进行判断，利用量子遗传算法的计算优点，选择较好的量子旋转门。量子旋转门的调整为：

其更新过程如下：

利用量子遗传算法对风门开度和燃烧器摆度进行优化调整，减少锅炉排烟含碳量和排烟氧量，从而使得锅炉燃烧效率和NOx排放量达到最佳。采用的适应度函数为：

式中：f′—理想锅炉燃烧效率；f—实际燃烧效率；［NOX］′—理想氮氧化合物排放量；［NOX］—实际氮氧化物排放量；α、β—燃烧效率和氮氧化物的加权系数，大小取决于效率和氮氧排放的比值。

量子遗传算法的计算流程图，如图4 所示。

图4 量子遗传算法的计算流程图Fig.4 Flow Chart of Quantum Genetic Algorithm

5 仿真实验

5.1 神经网络模型训练结果

利用表1 提供的燃烧特性实验数据，进行仿真计算。以锅炉燃烧特性为基础，构建一个单隐层的10 个输入和2 个输出的神经网络模型。其中神经网络的隐层和输出层分别采用线性函数和对数型函数，训练精度为0．0001，最大训练步数为2 000。

神经网络模型预测训练结果，如表2 所示。可以看出前10组训练样本数据，实际测量值与神经网络训练输出值误差不大。但从非训练的最后两组数据结果可以看出，对锅炉燃烧热效率和氮氧化物排量的神经网络预测的对比误差为0．8602%和0．5425%、0．9321%和 2．5438%，得到预测的结果之间误差较小，证明神经网络作为燃烧热效率和氮氧化物排量预测的模型，可以有效解决锅炉燃烧系统复杂模型问题。

表2 神经网络模型预测训练结果Tab.2 Neural Network Model Prediction Training Results

5.2 量子遗传算法寻优

采用量子比特编码长度为20，算法种群规模为40，选择一种量子旋转角度调整策略来实现优化操作，如表3 所示。

表3 旋转角选择策略Tab.3 Rotation Angle Selection Strategy

为了使锅炉燃烧效率和氮氧化物排放量过大影响整体的优化水平，必须同时兼顾两者优化的比值，取适应值函数系数分别为11.5 和0.15。由于工况氮氧排放最高，以环境污染的考虑，优化工况，仿真结果，如图5～图7 所示。仿真优化前后结果参数对比，如表4 所示。从表中可以看出，锅炉氮氧化物的排放有着显著的降低，同时燃烧效率有轻微的升高，证明通过量子遗传算法优化，可以实现炉燃烧效率和氮氧化物排放量整体优化。