大理石表面涂层与基体结合力的研究
2020-11-23王铮铮
赵 民,孙 晶,邵 萌,王铮铮
(沈阳建筑大学机械工程学院,辽宁 沈阳 110168)
1 引言
新型涂层行业迅速崛起,并逐步进入公共视野,作为一种新兴技术吸引公众目光。历经数十年的改善,如今已广泛应用于机械产品、电子产品、航天制造和建筑装饰等诸多领域,具有广阔的开发与应用前景。美国和日本正逐步研发豪华轿车表面漆膜、军事隐形、绝缘、光致变色、透明耐磨等新型涂层技术。文献[1]利用溶胶-凝胶法二氧化硅涂层,用以研究其对树脂-氧化锆粘结的影响,并研究分析了涂层结构以及涂层与基体的结合强度大小。文献[2]在各种基材上生产和制造超疏水复合膜的简单方法,研究石材保护的超疏水涂料的表面性能,进而增强石材保护。就国内而言文献[3]研究了纳米二氧化硅涂层的发展现状,对使用中存在的问题进行剖析,展望了涂层的发展前景。文献[4]详细介绍了纳米涂层的几种制备方法,探讨了纳米涂层的优越性和应用广泛性。虽然涂层的应用非常广泛,但是基体材料一般为不锈钢、陶瓷、碳化硅、晶体玻璃,在石材表面的应用与研究少之又少。由于天然大理石的主要成分是碳酸钙,一般都含有杂质,本身又属于中硬度材料,如果暴露在空气中易受到二氧化碳、碳化物、水气的作用,易被风化、酸蚀、溶蚀等,进而影响基材表面光泽度。对石材表面涂抹类似于薄膜质地的纳米涂层,使其既不影响大理石自身固有的色彩等属性,又可以改善易于溶蚀的缺点,进而完善大理石不适用于露天、阴暗潮湿等恶劣环境,使其在建筑材料中得到广泛应用。
2 大理石表面涂层的制备
选择正交试验的方法进行涂层的配比研究,可以在较少的试验次数下考虑较多的试验参数因素,得到大理石表面涂层与机体结合力试验所需要的涂层。
2.1 设计因素选择
影响涂层性能的因素有改性纳米二氧化硅、溶剂、环氧树脂、固化剂、改性剂的用量以及反应时间和反应温度等多种因素[5],根据实际试验操作和所借鉴参考资料等方面综合考虑,由于本试验在夏季进行,试验反应速率可以满足具体试验需求,活性剂为溶解剂,量的多少和时间长短影响较小,因此忽略这些因素。选用改性纳米二氧化硅粉末、环氧树脂、固化剂为试验的三个主要影响因素,每个因素分别选取三个水平,并根据实际剂量确定改性二氧化硅的用量4-6g、环氧树脂3-5g、固化剂4-6g,形成三因素三水平的正交试验[6]。
2.2 试验方案确定
根据实际因素和水平值的取值范围,确定准确的用量参数,选用标准正交表L9(33),具体的试验序号和因素安排,如表1所示。依据标准正交表数据中三个不同因素A、B 和C 的对应剂量,可以制备9 组不同的涂层,按照试验序号来编号,用来完成下述的试验。将9 种试件和未涂的原石作为试验对象,可以通过红外光谱分析的方法证明改性新涂层的成功制备,可以用来下述的试验研究。

表1 标准正交表Tab.1 Standard Orthogonal Table
3 涂层与基体结合力的分析
涂层与基体结合力是指表面涂层与基体大理石的粘结力[7-10]。划痕试验中摩擦系数和声发器突变时,涂层刚好被破坏裸露出基体,此时破碎力大小就是涂层破损的临界载荷。由于基体大理石的表面光滑,涂层与其粘结较难,具体结合程度尚未可知,需要通过试验进行检验。为此对已经制备好的9 种涂层样件进行划痕试验,测定不同硬质涂层与基体大理石结合力的大小。
3.1 划痕试验设备及原理
试验的设备为德国进口RETC 机器,即摩擦磨损试验机。本试验采用金刚石压头,压头自动下移实施线性加载,选择往复运动模块,对涂层表面施加压力,进行深入式磨削,最终划破表面涂层。同时带动粘贴于试件上的传感器做同向运动,将检测到声噪电信号转化为数字信号传回计算机,以数据表格的形式保存在计算机内。划痕试验机,如图1 所示。

图1 划痕试验Fig.1 Scratch Test
3.2 试验参数设定与图像采集
本次线性加载的范围为(40~100)N,加载时间为1min,加载速度为60N/min,行程为0.2mm/s,行走距离为1.2cm,加载频率为1Hz。试验完成后,9 种涂层表面均呈现出长度为1.2cm 深浅不一的沟痕,涂层完全被破坏,直接裸露出了基体大理石表面,甚至部分大理石已被金刚石压头划伤,通过肉眼可以观察到破损后9 种涂层外观形貌依次,如图2 所示。

图2 不同涂层破损形貌Fig.2 Different Coating Damage Morphology
当金刚石压头破坏涂层触碰到大理石,噪声明显增大,此时所测得的声噪系数突变,测得临界破碎力即为所求膜/基结合力,持续加载一段时间后,停止试验,可观察到涂层表面破损严重,有的甚至成块脱落。对上述不同配比涂层进行试验操作,可以得到不同声噪系数随施加载荷变化的曲线,利用数据处理找出声噪突变点得到与之相对应的临界结合,可以得到9 个结合力:F(1)=60.98N;F(2)=77.86N;F(3)=88.41N;F(4)=74.45N;F(5)=80.00N;F(6)=75.14N;F(7)=67.38N;F(8)=61.36N;F(9)=70.92N。
3.3 方差分析
方差分析是常用的数理统计的一种基本分析方法,是工农业生产和科学研究中分析试验数据中一种行之有效的分析方法。其特点是可以区分各个因素对应结果之间的差异,并且能精确地估计影响试验结果的各因素的重要程度,此外,还可以分析试验误差对试验结果的影响。
方差分析具体过程如下:
第一步:计算 T、CT 和 Q 值

修正项CT=T2/n=656.52/9=47888.03

第二步:求总的偏差平方和
ST=QT-CT=633.62
第三步:计算各因素的偏差平方
SA=QA-CT=184.72
同理可得:
SB=167.13;SC=254.27
第四步:计算误差平方和
SE=ST-SA-SB-SC=26.50
第五步:计算自由度
总自由度T:
fT=n-1=9-1=8
各因素自由度:
fA=r-1=3-1=2
同理可得:
误差自由度e:
fe=fT-(fA+fB+fC)=2
第六步:计算平均偏差平方和
各因素的均方为:
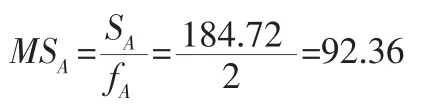
同理可得:MSB=83.57;MSC=127.14
误差均方为

第七步:计算各因素的F 值
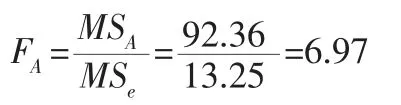
同理可得:FB=6.31;FC=9.60
第八步:F 值检验查F 分布临界值表得

方差分析结果表明:因素A、B、C 在水平上均显著,其中因素A 和B 即改性纳米二氧化硅和环氧树脂剂一般显著,因素C 即固化剂高度显著。因此,从提高结合力的角度考虑,可采取的办法是提高固化剂的用量,适当降低改性纳米二氧化硅和环氧树脂的量,预计会得到更加稳固的涂层。
4 结合力试验数据的回归分析
为了进行可行性分析,人们需要可预测的数学模型,即经验公式。数学模型的获得与建立较多的采用回归分析方法,它是处理变量相关关系的一种数理统计方法,通过对大量的数据进行处理,得出比较符合事物内部规律的数学表达式。
4.1 经验公式的建立
基于对多元线性回归分析和参数的最小二乘估计等一系列理论基础,对涂层的结合力大小做出以下回归分析。在回归的过程中,先采用软件Matlab 进行矩阵运算,得出回归的理想数学模型为指数形式,即设回归函数形式为:

式中:A,a,b,c—常数;F—涂层结合力(N);X 纳米二氧化硅(g);Y环氧树脂(g);Z 固化剂(g)。
对函数两边同时去常用对数,是其线性化可得:

由前面的理论和线性方程组的有关理论可得出:
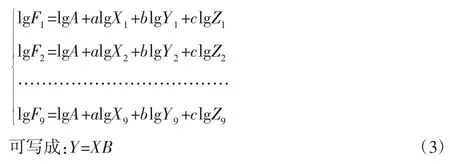
由以上数据求出结合力的数学模型,采用试验测得结合力的数据,对试验数据进行换算。将矩阵X 和Y 代入式(3)中,得到:

求得的回归系数 lgA=1.5842,a=-0.2805,b=0.2807,c=0.4386。可知涂层与基体结合力F 的经验公式为:

利用所求的公式(4)计算结合力F’,并将计算值与测量值的误差,如表2 所示。

表2 误差值表Tab.2 Error Table
由表格1 的误差值可知,所得计算值最大误差9.47%,最小误差仅0.10%,而平均误差为3.64%,在误差允许的范围内,根据以上计算结果可认为涂层结合力的预测数学模型与实际测量值拟合良好。由表1 中的误差数据绘制如图3 所示的结合力F 与实际测量值对比曲线,更加直观清晰的观察到二者的差别,同时也更客观地反应出数学模型的可行性。
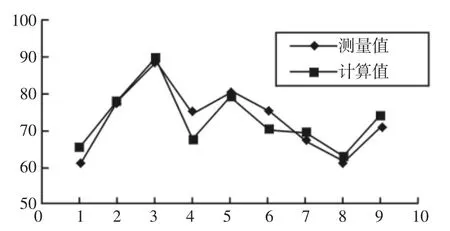
图3 F 计算值与实际测量值数据对比图Fig.3 Comparison Chart of F Calculated Value and the Actual Measured Value Data
4.2 显著性分析
在试验分析中,一个回归方程的效果如何,是否具有反映客观规律的实用性,可以通过数理统计的方法来检验,即对多元线性回归方程的数学模型和回归系数分别进行显著性检验。
4.2.1 结合力回归模型显著性校验
本试验结合力的预测模型只是一种假设,求出模型后需对其进行显著性检验,由此判断预测模型拟合程度的好坏。
回归模型转化为线性回归方程可表示:

为了进行数理统计检验,把总的偏差平方和进行分解,ST总的偏差平方和可分解为回归平方和SA和剩余平方和SE两部分,计算公式如下所示:
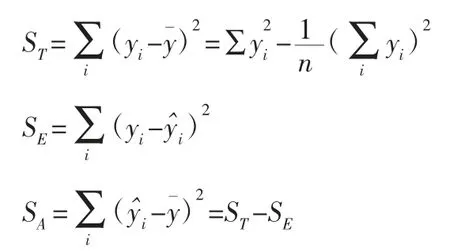
根据上述公式,分别求出:
回归平方和SA=0.01883835;
余平方和SE=0.0040876;
总的偏差平方和ST=0.02292595。
回归平方和ST所对应的自由度为自变量的个数M=3,总的自由度为N-1=8,所以剩余平方和SE的自由度为N-M-1=5。回归方程的显著性检验使用剩余平方和对回归平方和的F 检验法进行。
假设可采用统计量
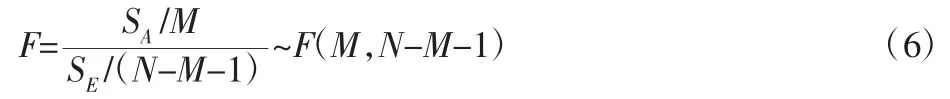
式中:N—试验组数;M—变量个数。
当F≥Fα(M,N-M-1)时,则认为回归方程在α 水平上显著,反之,没有显著意义。
根据式(6)求得 F=7.68。查分布表,当 α=0.05 时,F(3,5)=5.41。因为 F=7.68>F(3,5),所以涂层与基体的结合力回归方程是显著的。
4.2.2 结合力回归系数的显著性检验
假设可采用统计变量
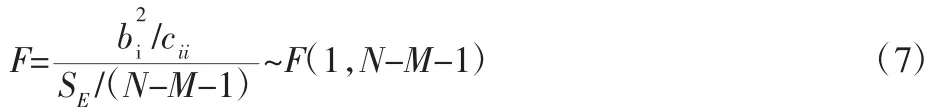
式中:Cii—原M 元回归的正规方程系数矩阵A 的逆矩阵C=(X′X)-1中的对角线上的第i 个元素;N—试验组数;M—变量个数。
根据式(7)计算不同回归系数F 值:
当 i=1,F=4.49;当 i=2 时,F=7.16;当 i=3,F=10.8。
由以上计算可知,β3>β2>β1。查 F 分布表,当 α=0.10时,F(1,5)=4.06;α=0.05 时,F(1,5)=6.61;α=0.01 时,F(1,5)=16.26。对比回归系数的F 值与所查的F 值的大小可知本试验考虑的三个因素参数对结合力影响均为显著。
5 结论
综合考虑,选用改性纳米二氧化硅、环氧树脂、固化剂为试验的三个主要因素,每个因素分别选取三个水平,安排了标准的L9(33)正交表。利用摩擦磨损试验机通过划痕试验测得9 个涂层试件的临界结合力值分别为 F(1)=60.98N;F(2)=77.86N;F(3)=88.41N:F(4)=74.45N;F(5)=80.00N;F(6)=75.14N;F(7)=67.38N;F(8)=61.36N;F(9)=70.92N。方差分析结果表明环氧树脂和固化剂一般显著,固化剂高度显著。同时利用回归分析建立了回归方程的数学模型,并求得了相应的经验公式,最大的误差为9.47%,最小为0.10%,平均误差为3.64%,最大误差在允许的范围内,所以涂层结合力的预测数学模型与实际测量值拟合良好。最后,利用显著性分析对回归模型和回归系数分别进行显著性检验,得出二者均对涂层结合力影响显著。
