一种利用非共面圆的相机标定和测量研究
2020-11-23崔东慧顾寄南唐仕喜
崔东慧,顾寄南,唐仕喜
(江苏大学制造业信息化研究中心,江苏 镇江 212013)
1 引言
无论是机械领域、能源领域,还是军事等其他领域,圆筒形的工件(管道)已经得到很大规模的应用。然而目前在圆筒生产过程中的检测或管道的检测,都是利用人工来完成的,其工作效率及检测的准确性有限。随着中国制造2025 的到来,智能化水平不断提高,机器视觉在圆筒形工件的内部检测领域获得了较为广泛的应用发展[5]。为了能够准确测量圆筒内部特征,首先应当精确知晓摄像机的内外参数,如焦距和图像中心坐标等。然而摄像机会因为检测过程中的移动以及光学自动调节焦距功能,其参数发生变化,所以检测前的预标定很多时候不能满足在检测精确度方面的要求[6]。
然而,由于在检测的图像采集过程中,摄像机能够采集到围绕圆筒内圆周方向的两个或多个圆形凹槽形成的椭圆轮廓,如图1 所示。且这些凹槽可以从设计图中获得。在这里提出了一种通过一幅图像中已知半径和相对距离的两个圆形凹槽进行摄像机标定的方法。最后通过模拟实验验证该方法的效果及其对噪声的鲁棒性。实验结果表明,该方法完全能够满足检测精度的要求。

图1 采集的管道视频图像Fig.1 Captured Video Image of Pipe
2 标定理论介绍
2.1 摄像机模型
将CCD 摄像机图像采集过程看作如下针孔摄像机模型:

式中:X=[X1X2X3X4]T—齐次坐标参考系中的点;X=[X1X21]T—齐次图像坐标系中X 的投影图像点;s—比例因子。矩阵K 是内部参数矩阵,其中包括焦距f1,f2和摄像机中心坐标c1,c2。矩阵R 是旋转矩阵,向量t 是图像坐标和世界坐标之间的平移向量。
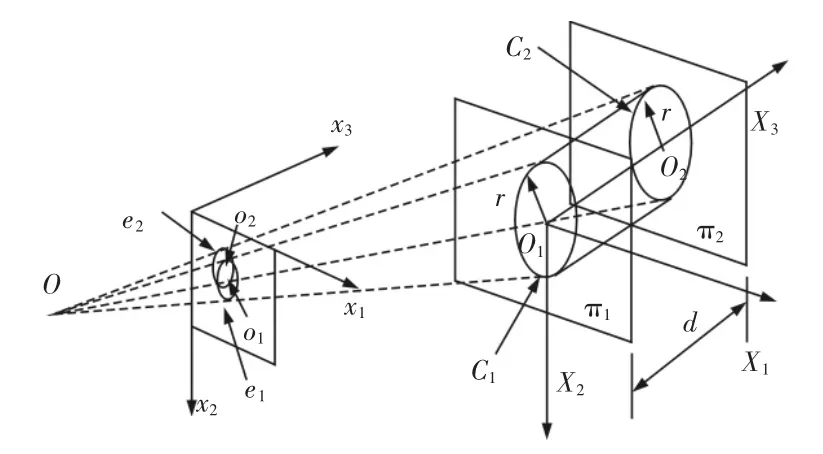
图2 圆形凹槽的图像信息Fig.2 Image Formation of the Circular Grooves
管道中的两个最大的圆C1,C2在图像平面投影成两个椭圆e1,e2,如图2 所示。假设两圆的半径已知,且都为r;同时两圆所在的平面π1和π2相互平行且两平面之间的距离为d。
2.2 绝对圆锥曲线、圆点、消隐点
两个圆C1,C2在齐次坐标系中可以表示为:

绝对圆锥曲线Ω 组成的图像点满足如下公式:

绝对圆锥曲线是摄像机标定的关键,其图像ϖ 组成的点满足包含内部参数矩阵K 的公式:

其中垂直于X3轴的平面的圆点Z1和Z2满足如下条件:
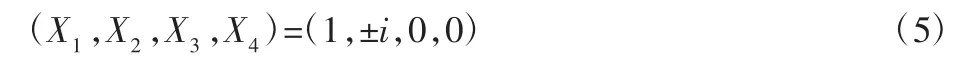
式中:i—虚数i2=-1。平面的圆点是垂直于X3轴的平面与绝对圆锥曲线的交点,他们是一对复共轭点。因此圆点Z1,Z2的图像点z1,z2仍然在绝对圆锥曲线ϖ 上,且满足:

消隐点v∞与圆点 z1,z2的图像满足“极-极关系”,消隐点是沿X3轴无穷远处点的图像,且满足条件:
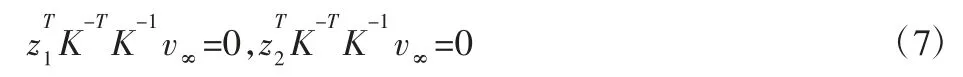
若能够确定圆点 z1,z2和消隐点 v∞,便可从式(6)和式(7)中求解出包含在内部参数矩阵K 中的四个摄像机内部参数f1,f2,c1,c2。
在前人的研究中,关于使用椭圆图像的摄像机标定方法通常基于同一平面上的多个圆或具有不同法线方向的多个平面上的多个圆[7-8]。可以假设在圆筒内的两个平面不是同一个平面并且具有相同的法线方向。
与这里方法类似的研究[9]利用饮料罐或圆柱形杯子的上部圆圈和下部圆圈进行摄像机标定,其大部分结果适用于这里的问题。但在其研究中,应该在图像中观察到连接上圆圈和底圆圈的左侧和右侧轮廓线,以确定消隐点v∞,如图3(a)所示。然而,在圆柱形管道内无法观察到轮廓线的真实图像,并且其解决方案不适用于这里的问题,如图3(b)所示。

图3 圆柱体的椭圆图像Fig.3 Two Ellipse Images in a Cylinder
在前人的研究基础上,提出一种利用圆筒内部两个椭圆图像确定消隐点并完成摄像机标定的方法。
3 摄像机标定方法
3.1 圆点的识别
垂直于X3轴的平面上的无穷远处的线由L∞表示,其由满足X3=X4=0 的点组成,并且对应于物理平面中的水平线。如下公式表示垂直于X3轴的平面上的任何圆C:

因此,圆点Z1和Z2是圆C 和无穷远处的线L∞的交点。圆C1和C2彼此在圆点 Z1,Z2处相交,并且圆的椭圆投影图像 e1,e2也在图像平面上的圆点z1,z2处相交。
因为圆点Z1,Z2是复共轭对,所以圆点z1,z2的图像也是复共轭对,并且不是实点,在实际图像中不能观察到。通常,由于椭圆在图像坐标系中是由二次形式表示,所以两个椭圆的交点的数量是四个,并且这些交点是四个实际点,或两个实数点和一对复共轭点,或者两对复共轭点。
在管道内部的图像中,找不到四个实际交点。在仅找到一对复共轭交点的情况下,这些点就是圆点的图像。但是,当找到两对复共轭交点时,这两对是与具有两个不同法线方向的两个平面对应的圆点图像。因此,有必要区分两对复共轭交点中的哪一个对应于实际环境,此问题将在后面解决。
3.2 消隐点的识别
由两个圆C1,C2组成的圆柱体的图像,如图5 所示。消隐线l∞是垂直于X3轴的平面的无穷远处的线L∞的图像。如果圆点z1,z2的图像被识别,则消隐线l∞也可以被识别,因为消隐线l∞是与两个点 z1,z2相交线。
在图 4(b)中,点 p 是消隐线 l∞上的任意点。令 e1,e2是椭圆图像e1,e2的3×3 矩阵表示。以点p 为极点,可以获得相对于椭圆e1的极线l1(=e1p),而线l2(=e2p)是点p 相对于椭圆e2的极线。点a1和 b1是椭圆 e1和线 l1的交点,点 a2和 b2是椭圆 e2和线 l2的交点。消隐点v∞可以通过线的交点获得。圆中心点的图像o1和o2也可以使用极—极关系获得,如下:


图4 圆柱体与其图像Fig.4 A Cylinder and its Image
3.3 摄像机参数的确定
识别出圆点后,则根据式(6)和式(7)可以求得摄像机内部参数,且剩余求取摄像机外部参数的过程(如从参考坐标系到摄像机坐标系的旋转和平移参数)与其他方法类似,详细过程可参考相关文献[10]。
4 实验与分析
4.1 模拟结果
为了验证标定算法,使用由给定标定参数生成的合成图像进行仿真。

图5 模拟结果Fig.5 Simulation Results
图5(a)和图 5(c)显示了生成的椭圆点,图 5(b)和图 5(d)显示了分别对应于图5(a)和图5(c)检测到的消隐点和椭圆中心。在图5(c)中,1%的随机噪声被加到圆C1和C2的半径上。对应于两组圆点分别获得两组消隐点,如图5(b)、图5(d)所示。表1 显示了在没有噪声和1%噪声半径圆的情况下获得的标定参数。旋转角度R1,R2,R3是用于组成旋转矩阵R 的三个角度,如下:

角度R3与给定值不同,不能重建为实际值,因为它不能在图像中使管道沿X3轴旋转。在两组标定参数之间,因为假定实际半径值是已知的,所以可以通过使用计算的半径来确定实际参数集。在表1 中,1 和2 的结果是正确的结果,因为它们的半径接近给定的半径值200mm。1*和2*的结果是具有相同椭圆图像的其他摄像机参数集。因此,可以通过半径值区分正确的摄像机标定参数,在参考文献[10]中的方式选择了一组作为实际集。

表1 模拟结果Tab.1 Simulation Results
4.2 实验结果
实验过程中使用了一个实验管道,其中有几个圆圈,它们之间的距离和半径内已知。使用了具有变焦功能的SONY FCBEX480 彩色CCD 摄像机,并使用DVR(数字录像机)以AVI 动画格式记录实验视频图像,并使用图像捕获软件从动态图像文件中捕获BMP 图像文件。采集到的图像有一些非线性镜头失真,这在这里的方法中没有考虑,此次通过使用Tsai 标定算法的预处理来恢复图像的失真。
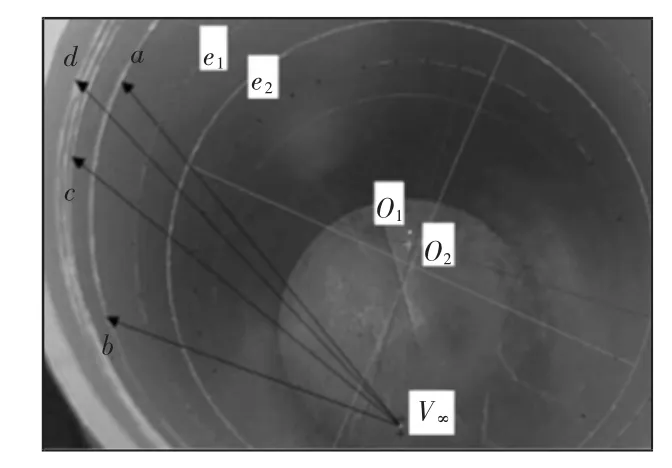
图6 实验管道中采集的图像Fig.6 Captured Image of the Inside of the Experimental Pipe
在实验管道内部采集的图像,并获得了标定参数,计算了参考圆C1和其他圆圈之间的距离,以验证所提出的方法,如图6 所示。表2 提供了点a,b,c,d 和圆C1之间的实际距离和检测距离。误差小于2mm,说明该方法是有效的,如表2 所示。

表2 点与圆C1 之间的距离Tab.2 Distances Between the Points and the Circle C1
5 总结
提出了一种从圆筒内使用两个椭圆轮廓的摄像机标定方法。通过仿真和实验结果表明,所提出的方法是能够满足标定相关要求。该方法可应用于圆筒形套管内部的缺陷定位和检测。
