基于全矢CEEMD 的轴承故障诊断研究

汪一飞，王鸣明，郝旺身，董辛旻

（郑州大学振动工程研究所，河南 郑州 450001）

1 引言

滚动轴承作为机械系统中的关键性部位，其运行状态在整个系统中起着决定运行状态优劣的关键性作用。因此，滚动轴承的故障诊断尤为重要。针对滚动轴承的故障信号的非平稳非线性的特点，1998 年文献[1]提出了一种时频分析方法：经验模态分解（Empirical Mode Decomposition，EMD），EMD 是一种专门用于处理滚动轴承信号的自适应非线性非平稳数据分析方法。但是，EMD依然存在一些问题，例如组件中存在着不同尺度的信号，或者在不同的IMF 组件中存在相似的尺度信号，称为“模态混叠”现象。为克服这些问题，文献[2]提出了一种补充的总体平均经验模态分解方法（Complementary Ensemble Empirical Mode Decomposition，CEEMD），将两组相反的白噪声信号加入原始信号，并对其进行EMD 分解，然后将得到的结果合并到最终的IMF 组件中。相较于总体平均经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）[3]，CEEMD 在保证了分解效果与之相当的前提下，抑制了由白噪声引起的重建误差，并且减少了迭代次数，并且降低了计算成本。

全矢谱技术通过采集水平和竖直方向的同源双通道信号并将其有效融合，弥补了单通道的振动信号的单一性和片面性。根据全矢谱和CEEMD 的特点，提出了全矢CEEMD 的故障诊断方法，得到的故障特征更加全面。并通过实例分析证明了此方法具有更好的效果。

2 基本原理

2.1 全矢谱理论基础

大型旋转机械通常在转子的同一截面安装两个相互垂直的传感器来提取振动信息，全矢谱具有可以将彼此垂直的振动信号特征进行融合，全面表示转子振动的强度和频谱结构的独特优势。其基本思想是转子的涡流现象是谐波频率的组合，其涡旋轨迹是一系列椭圆。定义椭圆的长半轴是振动强度评估的主要振动矢量，短半轴是振动强度的子振动矢量。而转子在不同谐波频率下的强度是对故障判别的基本依据[4]。设x、y 方向上的数据序列分别为｛Xi｝和｛Yi｝，其构成的复序列为｛Zi｝=｛Xi｝+j｛Yi｝（i=1，2，…，N/2-1），j 为虚数；通过傅里变换有｛Zi｝=｛ZRi｝+｛Zli｝×j，｛ZRi｝、｛Zli｝分别为｛Zi｝的实部和虚部。将椭圆的长轴Rai定义为主振动矢量；椭圆的短轴Rbi是副振动矢量，αi为主振动矢量和x 轴之间的夹角；φi为该频率下椭圆轨迹的初相位角。据傅里叶变换特性，可以得到下面的公式（推导过程参见文献[5]）。

2.2 CEEMD 基本原理

CEEMD 是一种基于经验模态分解（EMD）和总体经验模式分解（EEMD）提出的改进算法。EMD 算法将任何复杂的时间序列分解为有限数量的本征模函数（IMF）之和，每个函数反映原始信号的动态特性[6]。IMF 分量必须满足两个条件：（a）其极点数量和零点是相同的或者最多有一个不相同；（b）上包络线和下包络线关于时间轴局部对称。EMD 方法分解的基本原理是连续地去除信号的极大极小值的上下包络线的平均值，详细步骤为[7]：

（1）获得x（t）的所有最大和最小点数；

（2）在极值点之间插入样条函数3 次，得到上下包络线emax（t）和原始数据 x（t）在上下包络线之间；

（3）计算（2）中上下包络线的平均值线 m1（t）=［emax（t）+emin（t）］，用 x（t）减去

（4）以 h1（t）代替 x（t），重复上述 3 个步骤，直到 h1m（t）成为IMF 函数（满足上述条件（a）和（b）），并记

由EMD 分解的IMF 分量突出显示数据的局部特征，虽然完全摆脱了傅里叶变换的局限性，并且对于非平稳非线性信号极为适用。但当复杂的非线性和非平稳信号包含异常事件（如不连续信号，脉冲干扰，噪声等）时，EMD 将表现出模态混叠和能量泄漏现象，即不同频率尺度的信号存在于同一IMF 组件中以及类似频率尺度的信号出现在不同的IMF 组件中。

鉴于EMD 的缺点，文献[8]提出总体经验模式分解（EEMD），EEMD 是一种以噪声来辅助解决模态混叠问题的数据分析方法，即将白噪声添加到待分解的信号中，并利用白噪声频谱的均匀分布特性使信号在不同时间尺度上与白噪声混合，从而有效的解决了模态混叠问题。在原始信号添加白噪声之后，通过EMD 获得的每个IMF 分量被混合成一定比例的噪声分量，因此需要数百次EMD 分解来抑制或消除噪声的影响。因此，分解效率低，这影响了其在实践中的应用。文献[9]又提出了总体经验模式分解（CEEMD），意在为了提升EEMD 方法的计算效率，该方法在保持了EEMD方法的各种优点的前提之下，进而大大地加大了EEMD 方法的计算效率。CEEMD 包括以下几个步骤：

（1）在目标数据上加入白噪声序列n1（t）；（2）将混入噪声的数据进行分解，得到第一组固有模态函数 c1i，r1；（3）在（2）中的数据里加入与第一步符号相反的白噪声序列-n1（t）；（4）将混入噪声的数据进行分解，得到第二组固有模态函数c-1i；r-1；（5）将另一组白噪声序列添加到目标数据n2（t）中，并重复运行1，2，3，4，得到c2i，r2，c-2i，r-2，依次类推，得到 n 组 cnj，rn，c-nj，r-n；（6）计算所有分解得到的IMF 的（总体）均值作为最终的IMF 结果：

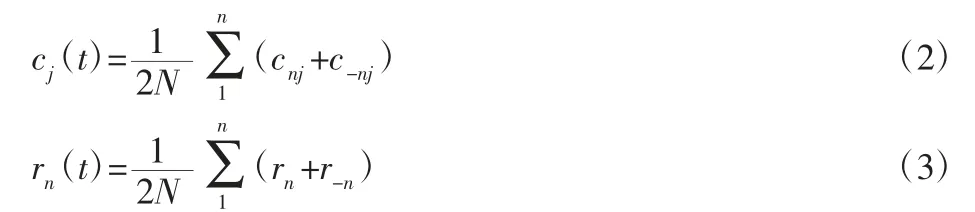
2.3 全矢 CEEMD 方法

（1）从相同截面获得的两个相互垂直的信号为 x（t）、y（t），将同源双通道信号进行CEEMD 分解，得到的IMF 分量；

（2）根据排列熵值选取有用的IMF 分量进行信号重构；

（3）将重构得到的信号进行全矢信息融合，并根据结果进行频谱特征分析，如图1 所示。

图1 CEEMD 方法流程图Fig.1 Flow Chart of CEEMD Method

3 实验结果分析

实验数据采用滚动轴承实测信号来进行分析，数据由美国辛辛那提大学智能维护中心提供[10]。选其中一组轴承内圈故障时的数据来进行处理和分析，实验装置，如图2 所示。实验台的轴上安装了4 个轴承，通过摩擦带将转速连接到轴上的转速保持恒定在约2000r/min，将6000lbs 的径向载荷通过弹簧机构施加到轴和轴承上，所有轴承都采用强制润。滑轴承型号为Rexnord ZA-2115 的双列滚子轴承，每列包含16 个滚动体，节圆直径为71.5mm，滚子直径为8.4mm，接触角为15.17°。实验中在每个轴承的相同截面安装两个方向互相垂直的PCB 353B33 高灵敏度石英ICP 加速度传感器来采集振动信号，采样频率为20kHz，采样长度为20480 点。我们选取其中一组轴承3 内圈故障时的数据来进行处理和分析，根据转速及轴承参数，可以计算出轴承3 内圈故障频率为294Hz。对于这类非平稳故障信号，之前的研究者大多使用EEMD 对其进行信号处理，但存在信号重构效率较低，不准确，有局限性等问题。分别用EEMD 和CEEMD 对该数据进行预处理，其中，噪音标准偏差为0.2，实现次数为500，最大迭代次数为5000。通过EEMD 和CEEMD 进行分解得到的IMF 分量，如图3 所示。从图中可以看出，两种方法分解出的IMF 分量里，除IMF1 之外，EEMD 分解得到的其余IMF 分量振动信号较弱，振幅很低，因而包含的有效信息不完整，这将影响到重构得到的信号所包含故障信息的完整性。

图2 实验台整体结构示意图及局部照片Fig.2 Schematic Diagram of the Whole Structure and Partial Photos of the Experimental Bench

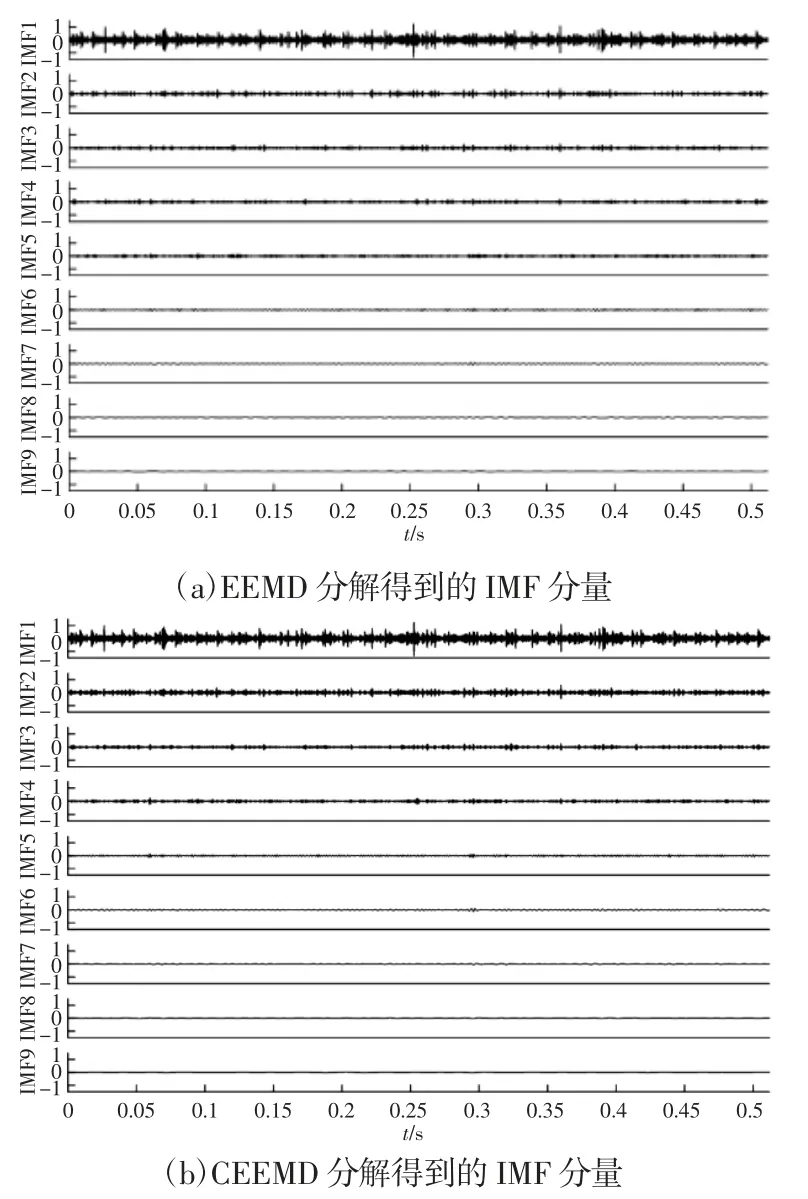
图3 两种方法分解得到的结果Fig.3 Shows the Results of the Decomposition of the Two Methods

与EEMD 相比，CEEMD 方法的优点是分解得到这些IMF分量的筛选迭代次数很低。EEMD 需要278931 次筛选迭代，而CEEMD 只需要140939 次，几乎是EEMD 的一半。很明显，CEEMD 在计算成本方面有很大的改进，只需要EEMD 一半的筛选迭代次数就可以得到这个信号。两种方法的每个点所需的筛选迭代次数的箱型图，如图4 所示。

图4 显示每个模式的筛选迭代次数的箱型图Fig.4 Shows a Box Diagram Showing the Number of Filter Iterations Perpattern

对CEEMD 分解得到的IMF 分量进行排列熵值计算，如表5所示。可知，从第5 个IMF 分量开始，其排列熵值依次下降较明显，因为所选信号为轴承内圈故障信号，信号复杂性高，也更具有随机性，故全矢排列熵较大，即第四个分量之后包含有效信息较少，所以选择前四个IMF 分量进行信号重构。

表1 计算得到的各IMF分量的PE 值Tab.1 The PE Values of IMF Components Calculate

我们把IMF 分量相加来进行信号的重构，并且为了更加清楚直接的看到轴承的故障特征，我们需要对两个垂直方向的重构信号分别进行Hilbert 解调求包络谱，即滚动轴承的故障诊断中常用的包络分析法。X、Y 通道的包络谱，如图5 所示。由图5（a）、图5（b）可以观察到，得到的水平通道和垂直通道的CEEMD 包络谱差异较为明显，其所包含信息有所不同，X 通道除了在基频的二倍频2fr=66Hz 处振动较为强烈外，其余特征频率的振动强度都比较弱。Y 通道的信号在故障频率f=294Hz 和二倍频2f=588Hz处振动强度较大，在33Hz、521Hz 处振动强度相对较弱。虽然信号是来自同一截面的两个不同方向的同源信息，但是其包含信息具有差异。因此，我们依据全矢Hilbert 原理，将双通道的同源信号进行全矢融合，融合后的信号包含了双通道同源信号的各自特点，保证了提取信息的全面性，不会出现因为选择通道的不同而导致特征提取的结果不同的情况，经过全矢信息融合得到的新包络谱，如图6 所示。从中可以清楚的看到故障频率f=294Hz 和二倍频2f=588Hz 及转频的调制频率621Hz。由此可以证明由全矢融合后得到的包络相较于单通道得到的包络，可以使提取的轴承故障特征更加准确和全面。

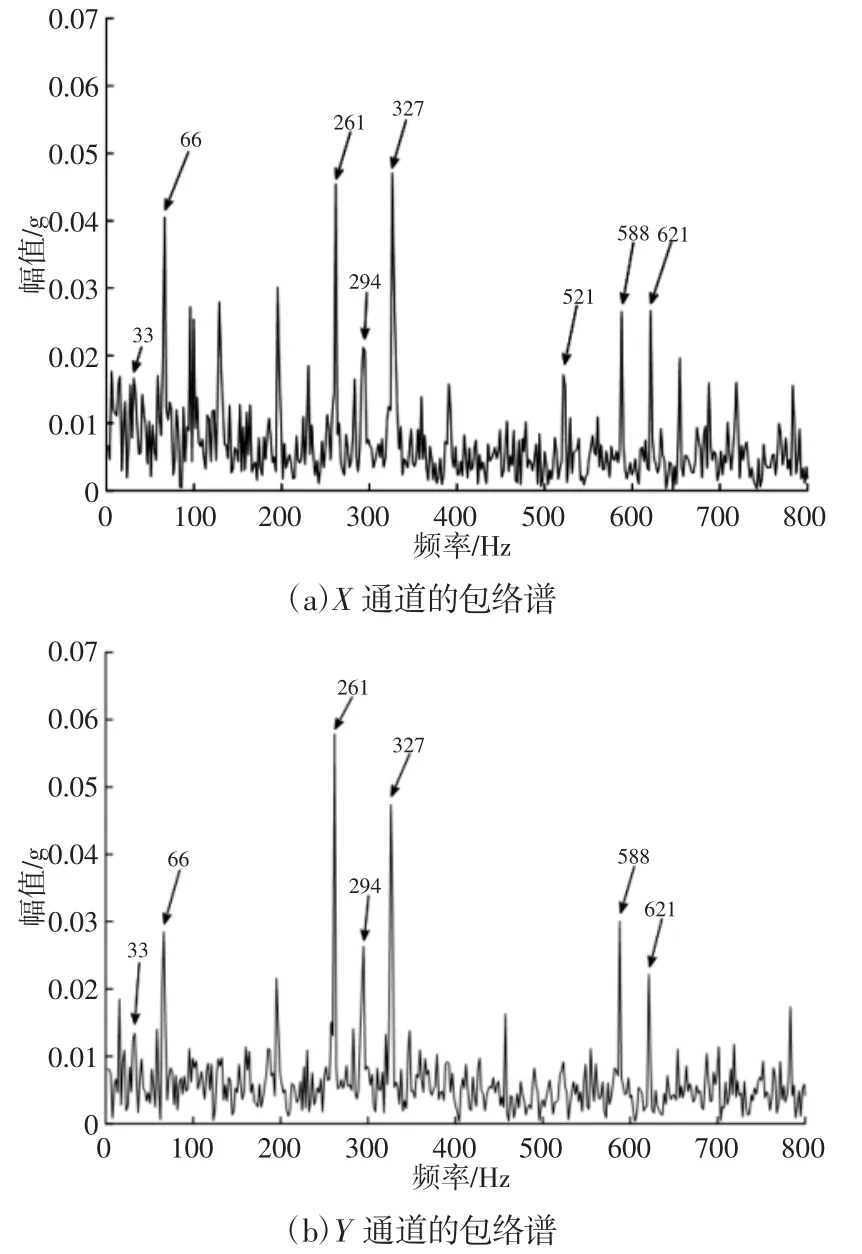
图5 X、Y 通道的包络谱Fig.5 Envelope Spectrum of X and Y Channels

图6 全矢融合双通道的包络谱Fig.6 Envelope Spectrum of Full Vector Fusion Two-Channel

为了更加直观的显示出数据分析结果，我们列表进行各频率的幅值对比，如表2 所示。

表2 两种方法各频率的幅值Tab.2 The Amplitude of Each Frequency in the Two Methods

由上述可知，上述全矢CEEMD 方法不仅提高了诊断效率，而且避免了传统单通道分析方法获取信息单一的缺点。

4 结论

通过对美国辛辛那提大学智能维护中心提供的出现内圈故障的滚动轴承3 的实测信号进行了CEEMD 分解，利用计算排列熵值的大小来筛选有效IMF 分量进行型号重构，结果显示，CEEMD 具有比EEMD 分解得到的IMF 分量质量更好，并且所做的筛选迭代次数减少了一半，从而大大节省了计算成本，并且通过对IMF 分量的叠加可以精确地重构原始信号。将全矢谱信息融合与CEEMD 相结合，解决了传统单通道方法的单一性。与传统信号处理方法相比，提出的方法对信号的重构效果较好，并且计算成本低，可以快速精确的获得重构信号，同时，全矢CEEMD提取的故障特征更加准确、全面。