局部均布荷载作用下四边支承矩形板的内力计算

杨成永，马文辉，韩薛果，程霖

（北京交通大学 土木建筑工程学院，北京 100044）

地铁、热力和燃气等地下工程中，地下构筑物的顶板多为四边支承的薄板，板上常承受局部均布荷载如汽车轮压作用.为了确定像汽车轮压这类荷载在板内产生的最大挠度和内力，需要进行任意位置局部均布荷载作用下挠度和内力的计算.

对四边支承的矩形薄板问题，可以从四边简支板的Navier 解出发，采用叠加方法[1-2]或加补充项的方法[3-4]解决.如：蔡长安等[5-6]以带附加补充项的Fourier 级数作为挠度函数，求解了Winkler 地基及Pasternak 地基上自由边矩形板的弯曲问题.许琪楼等[7-8]采用一种能满足自由角点条件的挠度表达式，解决了二邻边支承二邻边自由矩形板和二邻边及对角点支承矩形板的弯曲问题.他们还采用叠加方法[9-10]，提出了四边支承矩形板及一边固定一角点或二角点支承的矩形板的统一求解方法.岳建勇等[11-12]采用一种双三角级数形式的挠度函数，得到了三边固定一边自由及两对边固定两对边自由矩形板的精确解.钟阳等[13]在辛几何空间中利用分离变量法推导出了四边固支弹性矩形薄板的精确解析表达式.于天崇等[14]假定矩形板的抗弯刚度沿板的宽度方向按照一般幂函数形式变化，研究了四边简支一对边受弯作用下面内变刚度矩形板的弯曲问题.肖闪闪等[15]采用载荷叠加法研究了集中载荷下四边固支正交各向异性矩形板的线性弯曲，并讨论了经典Kirchhoff 薄板假设对于集中载荷的适用性.

可以看出，目前已有的研究成果中，叠加方法应用较多.而补充项的方法公式简单，能够对各种边界条件进行统一处理.

既有研究工作存在以下不足：1）没有直接给出局部均布荷载作用下四边支承板内力计算公式，致使工程技术人员在实践中对级数解的研究成果难以利用.2）对级数解的收敛速度讨论不充分，不清楚究竟需要取多少项级数才能满足精度要求.3）级数解与有限元数值解在计算精度和速度方面没有进行仔细对比.不了解两种解法在精度上能达到多高的吻合程度；不清楚级数解法的计算速度比有限元法具体快多少.

为了探讨上述问题，本文采用补充项方法进行四边支承板计算，提出了挠度及弯矩的计算公式；讨论了解法的收敛速度，并与既有文献进行了求解结果正确性的验证；最后与有限元数值结果在求解精度和计算量上进行了对比.

1 微分方程及右端荷载

采用图1 所示的坐标系.图中a、b 为板的长度和宽度，m；x0、y0为局部均布荷载中心的坐标，m；c、d为局部均布荷载的分布长度和宽度，m.

图1 受局部均布荷载作用的矩形板Fig.1 A rectangular plate under locally uniformly distributed load

2 挠度和弯矩计算

对不同支承条件下的矩形板，文献[3]给出了带补充项的挠度表达式.针对本文的四边支承矩形板，有简化的挠度表达式为：

3 待定系数的确定

公式（5）～（10）中待定系数Aj、Bj、Ci、Di需要根据板边的支承条件确定.由于Aj、Bj、Ci、Di分别为左边、右边、前边及后边法向弯矩正弦级数的待定系数，因此当板的某边为简支边时，按公式（8）可知，相应的待定系数取为0.某边为固支时，按如下方法计算待定系数.

当板左边（x=0 边）为固支时，由式（4）在x=0处取w 对x 的偏导数：

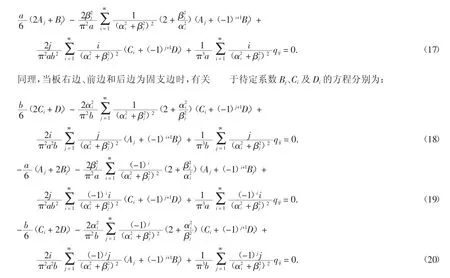
在利用公式（17）～（20）确定待定系数Aj、Bj、Ci、Di时，若某一边、某二边甚至某三边为简支，则舍弃相应的方程，留下剩余的方程组成方程组解出待定系数.以板左边及前边固支其余两边简支为例，此时由于右边和后边简支，故待定系数Bj=Di=0；舍弃公式（18）及（20）所列方程，剩下公式（17）及（19）所列方程组成方程组，并且在留下的方程中，置Bj及Di为0，进而解出左边及前边两个固支边的待定系数Aj和Ci即可.

4 计算与分析

4.1 计算步骤

采用本文公式计算四边支承板挠度和弯矩的步骤如下：

1）若板的四边全为简支边，则取Aj=Bj=Ci=Di=0.若板存有固支边，则从公式（17）～（20）中选择相应的公式组成方程组，计算待定系数Aj、Bj、Ci或Di.

2）确定系数Aj、Bj、Ci及Di后，按公式（7）计算挠度的傅里叶系数wij.

3）最后，按公式（4）计算挠度，按公式（9）及（10）计算弯矩.

本文后续计算中，线性方程组的求解采用克劳特（Crout）分解法.计算程序采用C 语言编写，程序中实型变量采用双精度.

4.2 计算参数

取板沿x 方向长度a=5 m，y 方向长度b=7 m，厚h=0.1 m；板弹性模量E=3×107kPa，泊松比μ=0.3；荷载按公路桥涵设计通用规范（JTG D60—2015）取一个汽车轮压传递到板上形成的局部均布荷载.轴重取120 kN，单轮地面分布尺寸0.6 m×0.2 m，轮压扩散角35°，板埋深0.714 m.由此得作用在板上的局部均布荷载q0=31.25 kPa，荷载x 方向分布长度c=1.6 m，y 方向分布长度d=1.2 m；荷载中心坐标x0=2.5 m，y0=3.5 m.

4.3 收敛速度的讨论

采用4.2 节的计算参数，板四边均固支，取级数项数为5 项、10 项、20 项、30 项、40 项、50 项、60 项及80 项，计算结果列于表1.

表1 及后续表格中，“板中心挠度”“板中心x 方向弯矩”“板中心y 方向弯矩”“长边中点x 方向弯矩”分别为无量纲量

从表1 看出，30 项后，挠度计算结果的前5 位有效数字不再发生变化；40 项后，弯矩计算结果的前4位有效数字不再发生变化.因此可得出，40 项时，级数已可视为收敛.后续计算中采用40 项级数的计算结果.

表1 不同级数项数的计算结果Tab.1 Computed results by different number of series terms

4.4 计算结果与既有文献对比

4.4.1 与文献[1]对比

文献[1]中有四边固支板受满布均布荷载作用的计算结果.为与之对比，采用4.2 节的计算参数，板四边均固支，荷载改为满布，荷载强度不变，仍为q0=31.25 kPa.计算结果列于表2.

表2 与文献[1]计算结果对比Tab.2 Comparison of computed results with that in reference[1]

由表2 看出，2 种方法的结果前2 位有效数字相同.由于文献[1]表格的有效数字只有3 位，可以认为表2 中2 种结果是一致的.

4.4.2 与文献[16]对比

文献[16]列出了四边简支板中央受局部均布荷载作用时弯矩的计算系数.为与其对比并避免查表计算中的插值，取泊松比μ=0，轮压x 方向分布长度c=2 m，y 方向分布长度d=1 m，其余参数采用4.2 节的数据，板四边均简支.

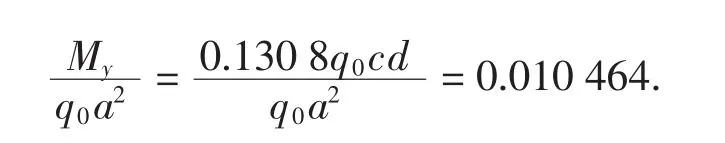
计算结果列于表3.

表3 与文献[16]计算结果对比Tab.3 Comparison of computed results with that in reference[16]

由表3 看出，两种方法的结果，前3 位有效数字相同.由于文献[16]表格的有效数字是4 位，可以认为表3 中两种结果是一致的.

4.5 计算结果与有限元对比

采用4.2 节的计算参数，板左边（x=0 边）及前边（y=0 边）固支，其余两边简支.按相同的参数和边界条件采用ANSYS 软件SHELL63 号单元，划分3种粗细不同网格进行计算.计算结果列于表4.

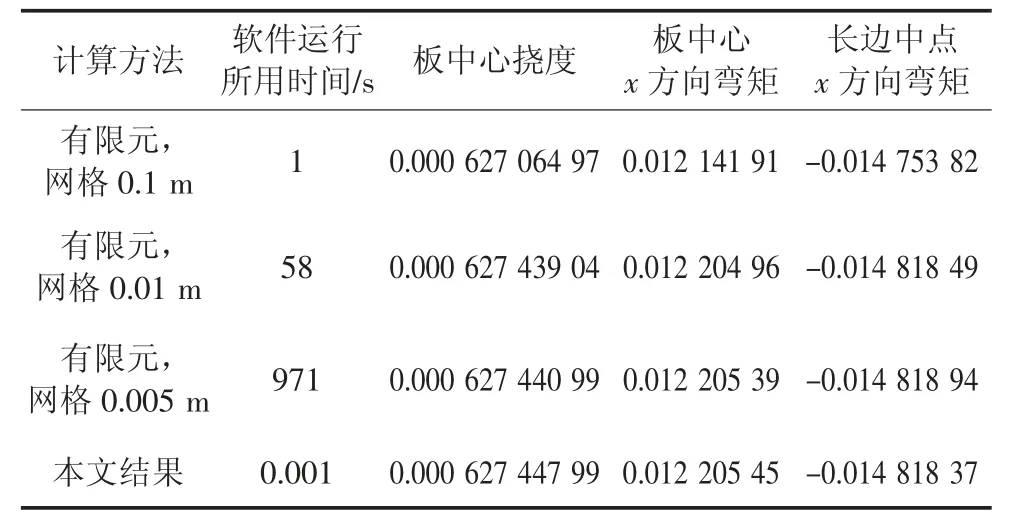
表4 与有限元计算结果对比Tab.4 Comparison of computed results with that by FEM

由表4 可看出：

1）随有限元网格的加密，计算结果逐渐趋于本文的级数解.由此可说明，本文级数解是四边支承板变形问题的理论解或精确解.当有限元网格细到5 mm×5 mm 时，挠度及弯矩有5 位有效数字与级数解相同.可以认为这时数值解与级数解基本一致.

2）表4 中的软件运行所用时间是从数据输入到输出全部的计算机运行时间.要达到较高的精度，有限元需要花费的计算机时间大大高于级数解.就本算例来说，相差达10 万倍以上.需要注意的是，本算例中，有限元在5 mm×5 mm 网格时，需要求解的方程组的阶数，不少于（x 方向节点数5/0.005）×（y 方向节点数7/0.005）×6 个自由度=840 万；而级数解取40 项时需要求解的方程组的阶数仅为40×2 个固支边=80.

5 结束语

采用带补充项的挠度函数，研究了四边支承矩形薄板的弯曲问题.给出了局部均布荷载作用下简支边和固支边不同组合条件下的统一计算公式.

对比计算表明，以Navier 解为基础带补充项的傅里叶级数解，达到收敛的级数项数约为40 项.该级数解与其他采用叠加法得到的傅里叶级数解，具有同样的求解精度.与有限元数值法相比，级数解的计算量十分微小.

值得一提的是，式（3）若换成满布荷载、线荷载和集中力相应的傅里叶系数，本文方法也适用.