桥梁固定式防撞钢套箱能力曲线的解析计算方法
2020-11-21樊伟张泽文申东杰孙洋
樊伟,张泽文,申东杰,孙洋
(1.湖南大学 土木工程学院,湖南 长沙 410082;2.风工程与桥梁工程湖南省重点实验室(湖南大学),湖南 长沙 410082)
随着航运业的快速发展,船桥矛盾日益突出,发生恶性船撞桥事故的概率也随之升高.据统计,船舶撞击是位列洪水之后航道桥梁倒塌的第二主因[1],船舶撞毁桥梁的问题已成为桥梁工程界面临的尖锐问题之一[2].因此在设计通航水域桥梁时,必须考虑船撞问题[3].我国《公路桥涵设计通用规范》(JTG D60—2015)中规定:“可能遭受船舶或漂流物撞击的桥墩,应考虑船舶或漂流物的撞击作用,并应设置警示标志和必要的防撞设施.”[4]为避免由船舶撞毁桥梁所带来的经济损失、人员伤亡,保护有可能遭遇船舶碰撞的桥梁下部结构,给桥梁布置合理有效的防撞装置显得尤为重要.樊伟[5]对国内外桥梁工程实例调研统计得出:美国、加拿大等国家多采用独立式防撞系统作为桥梁防撞的主要措施,然而与之不同的是,出于对经济性和适用性的考虑,我国越来越多的建设桥梁均采用钢结构护舷(钢套箱)形式的防撞装置,如苏通大桥[6]、金塘大桥[7]、武汉天兴洲大桥[8]、台州椒江二桥[9]及杭州湾跨海大桥[10]等.在船桥碰撞事故中,桥墩防撞装置(钢套箱)是抵御撞击的重要结构,因此对钢套箱的抗撞性能研究应给予足够重视.
船撞桥问题的研究起源于船船相撞的研究,其研究方法也大多借鉴船船相撞计算理论研究方法[11],大致分为:经验静力法、试验方法、精细有限元数值模拟方法和解析计算方法.
由于桥墩结构抗冲击的足尺试验代价太大,难以展开,因此这方面的试验研究并不多见[12].目前,国内外多采用数值模拟方法研究桥梁防撞击问题.如许薛军等[13]通过有限元软件建立船舶撞击桥墩的仿真模型,分析防撞套箱、橡胶护舷、桥墩之间的能量转换及防撞套箱撞击部位的受力与变形.Jiang等[14]利用有限元技术对一个浮式防撞钢套箱进行了全面深入的性能评估.Wang 等[15]对一种新型柔性防撞钢套箱展开数值模拟分析,并通过对缩尺模型进行一组落锤试验来验证数值模拟方法的正确性.有限元数值模拟方法精度高、适用性广,是目前钢套箱性能研究的最常见方法.
解析计算方法的优点为计算快速、所需参数少且计算结果相对准确.采用精细有限元技术费时费力,因而在防撞装置设计中应用受到限制,尤其在设计前期方案过程中,更不适合用于开展系统而详细的影响因素分析以及设计优化等[5].相比于精细有限元数值模拟方法,在船桥碰撞中解析计算方法目前应用较少,尤其是针对桥梁防护装置.以往船船碰撞解析计算研究中所采用船舶排水量多为万吨以上[16-17],钢套箱与此类船舶舷侧结构存在着尺寸差异,且实际工程中造型多为流线型,因此,通过在船侧结构碰撞机理的原有解析研究基础上建立适合钢套箱的简化分析方法,从而准确快速地推导出船舶撞击钢套箱的撞击力(能量)-撞深曲线,将在桥梁防撞装置的初步设计阶段,大大提高设计效率.
近年来学者们大多针对带球艏船舶的撞击展开分析研究,而楔形艏作为一种常见的艏部形状,与其相关的碰撞研究未得到足够重视.且钢套箱的变形损伤与撞击船艏的形状有着密切的关系,作为两种最为常见的船艏构造,研究两类不同船舶撞击下桥梁防撞装置的抗撞性能具有重要意义.
本文基于国内外学者对船舶舷侧结构中板材在不同受力情形、不同破坏模式下的解析计算研究,提出了一套合理、完整的应用于船舶撞击桥梁钢结构护舷(钢套箱)抗撞性分析的解析计算方法,并针对带球艏船舶、楔形艏船舶两类不同外形船艏结构的撞击开展研究,扩大了解析计算方法的适用范围.同时,采用精细有限元技术对船舶撞击钢套箱进行精细化建模计算.通过比较有限元软件计算出的撞击力(能量)-撞深曲线与解析计算结果,在保证简化分析方法快速性的同时,验证了该方法在桥梁防撞装置初步设计阶段的准确性、适用性.
1 钢套箱构件变形机理分析
传统的钢套箱结构多为板架构件,通常由竖向外板、顶板、底板、纵横舱壁、加劲肋等组成,当船舶开始接触钢套箱并向前行进时,随着撞击深度的增大,各个构件参与碰撞并通过自身的变形损伤(撕裂、断裂、压弯和屈曲等)来充分吸收撞击能量.
在船舶撞击钢套箱解析计算中,分别对竖向外板的撕裂、纵横舱壁的屈曲、加劲肋的弯曲断裂等构件破坏行为的变形机理进行解析计算,最后将各个构件的吸能性能整合在一起,得到整个钢套箱在撞击过程中的能量-撞深曲线.
1.1 外板遭遇刚性球体挤压阻力计算
Wang 等[18]曾根据球鼻艏外形运用塑性力学中的上限定理提出了外板抵抗球艏船撞击的简化力学模型,如图1 所示.

图1 球形刚体挤压下外板变形示意Fig.1 Deformation of outer plate under extrusion of a rigid ball
边界为2R 的圆形外板受半径为r 的刚性球体撞击下,在其未破裂前撞击力和撞击深度关系如下:
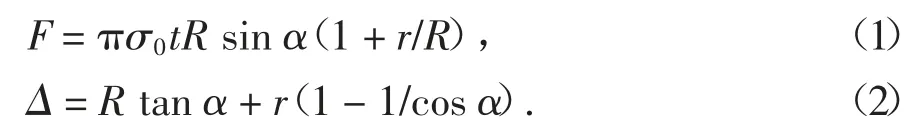
式中:σ0为材料的流动应力,通常认为是材料的屈服强度和极限强度总和的一半;R 为外板的变形区域半径;r 为球艏简化后得到的刚性球半径;t 为板的厚度;Δ 为撞击深度.
当r 远小于R 时,可将刚性球体视为一点,其荷载形式为点荷载,如图2 所示.上述公式可简化为式(3)形式.

通常情况下,球鼻艏的球鼻部分较尖锐,采用式(3)计算外板变形阻力更为方便快捷.

图2 点荷载作用下外板变形示意Fig.2 Deformation of outer plate under point load
1.2 外板遭遇楔形刚体挤压阻力计算
孙斌等[19]针对楔形艏撞击船舶舷侧外板进行了研究,将外板损伤变形的能量耗散分为膜拉伸能量耗散和两边塑性铰线的弯曲变形能量耗散,建立了外板在楔形船艏撞击下的解析计算公式:

式中:L1和L2为撞击点距离外板变形区域左右边界的距离;H 为变形区的高度;各角度标注如图3 所示;M0和N0分别为单位长度板条梁的极限塑性弯矩和极限塑性力,大小分别为:

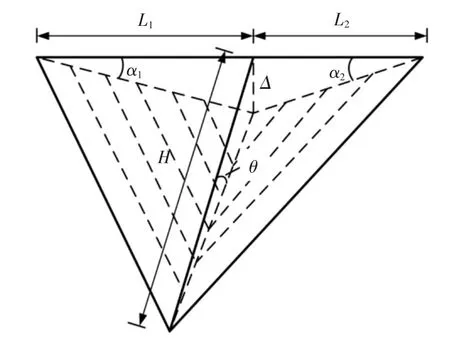
图3 楔形体挤压下外板变形示意Fig.3 Deformation of outer plate under extrusion of a wedge
1.3 板的面内撕裂阻力解析计算
Ohtsubo 等[20]对船舶在接地过程中船底外板遇到楔形体撕裂问题做了研究.假设板材的断裂是由韧性破坏引起的,认为在板材撕裂过程中塑性变形和摩擦是耗能的主要因素,而断裂是次要的,从而推导出板材撕裂问题的一种上限解,解释了板材撕裂过程中的破坏机理.
外板在受到角度为2θ 的楔形体撞击下,其撕裂过程中的阻力分为瞬时撕裂力Fp和摩擦力Ff,其中Ff为Fp在摩擦位移方向上的投影.最终获得的板材面内撕裂过程中力-位移关系为:
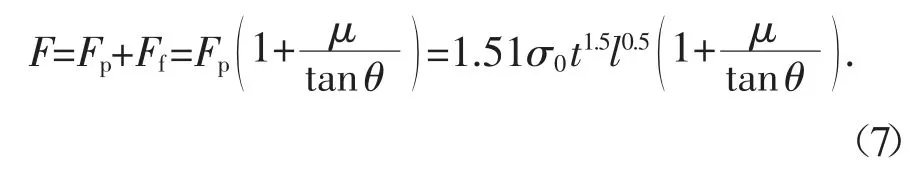
式中:σ0为流动应力;t 为板厚;l 为撕裂长度;θ 等于楔形体角度的1/2;μ 是摩擦因数,其值为0.15~0.3.
1.4 板的穿透模型阻力解析计算
Wang 等[21]经过一系列的试验证实了在穿透过程中外板破裂后仍具有一定的承载力,且其破坏模式与板的面内撕裂阻力解析机理极为相似,均涉及到了被撞击物前端尖角处较大的膜拉伸以及较远端的显著弯曲.根据公式(7)得到板破裂后其承载力与撞击深度的关系式如下:
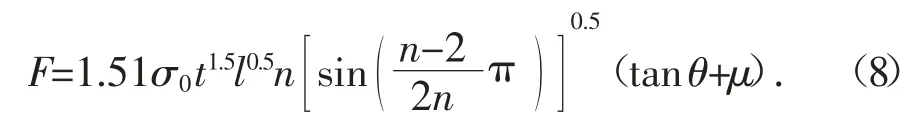
式中:l 为每一道裂缝的长度;n 为裂缝的条数;(n-2)π/n 为相邻裂缝之间形成的角度.当撞击物前端过于尖锐时(例如锐利的球艏或楔形艏),相邻两道裂缝形成的角度依附于前端的夹角2θ,即(n-2)π/2n=θ.一般尖锐的前端撞击外板会形成的裂缝数目为n=2,此时(n-2)π/2n=0 并不适用,将θ 代入原公式较为合适[17].
1.5 肋板折叠模型阻力解析计算
图4 所示为肋板折叠模型简图,Liu 等[22]在原有研究的启发下进一步建立了更为合理的解析模型.提出了新的肋板简化分析方法,给出了肋板在压碎过程中初始及后续折叠更为精确的阻力计算公式,将一个完整的折叠变形区域设为3H0,当b1=b2=b时,第一道折叠过程中平均压碎力大小为:


图4 肋板折叠模型Fig.4 Folding model of the ribbed plate
1.6 十字板压碎模型解析计算
钢套箱内部有非常多的横肋、竖桁相互交错,从而形成十字板的结构.Zhang[11]对十字板的阻力进行了解析计算研究.其破坏模式类似于肋板压碎破坏(如图5 所示),将第一道折叠区域设为2H1,其中H1=1.103(tb)0.5,在原有解析计算的基础上推导出了X形、T 形、L 形多种不同截面形式的纵、横梁组合结构受压下在第一道折叠过程中的平均变形阻力.

图5 十字板压碎模型Fig.5 Crush model of X-type plate

b 为十字板交点到边界的距离,即纵(横)肋长度的一半.当十字板结构在第N0道折叠中发生破裂后,假设阻力维持恒定,其后续的平均压碎力为:

通过给定钢材的断裂应变,可以计算出构件在第几道折叠中破裂,即N0的值.
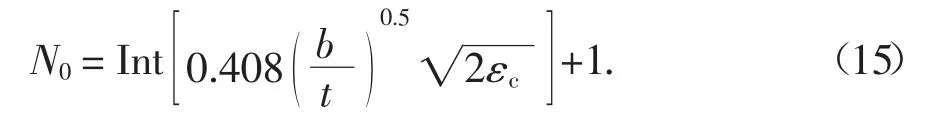
2 钢套箱抗撞性能的解析计算方法
2.1 计算方法基本假定
在解析计算方法中通常会适当引入一些合理的假设[23],这些基本假设简化了结构真实受力下的复杂性,便于快速有效地建立结构理论模型.结合桥梁防撞钢套箱的构造特点,归纳出适合于钢套箱抗撞性分析中的基本假定如下:
1)保守地假定船艏为刚体,依靠钢套箱的变形来吸收能量.
2)假设船艏以恒定速度沿着撞击方向持续前进,不考虑速度变化.
3)不考虑钢套箱内部各构件的相互作用,假定彼此之间的阻力是独立的.
4)各构件的力学模型中,假定以没有发生变形损伤的其他构件作为局部受力破坏的边界.
5)计算撞深最大为钢套箱内、外板间距.在船舶撞击钢套箱的过程中,内板已与桥墩紧密贴合,没有变形空间.
2.2 不同船艏外形下的碰撞情景
不同的船艏外形在与钢套箱的碰撞过程中接触到其内部各个构件时的撞击深度不同,意味着各个构件参与受力并耗散能量的撞深时刻会随着船艏的外形而发生变化;另外不同外形船艏撞击下钢套箱的损伤面积也会受显著影响,其参与耗能的构件数目、各个构件损伤程度都会有明显差异.为了便于研究,采用了文献[11]中提出的假定球鼻艏与楔形艏模型对碰撞情景进行说明,两种船艏的简化模型如图6 所示.

图6 两种典型船艏简化模型Fig.6 Simplification models of two typical bows
假定的球鼻艏模型主要参数包括上甲板楔形夹角2θ、船艏高度Hdeck、首柱倾角φ 以及球鼻处半椭球体3 个半径RL、RV、RH.由于半椭球体是最先接触且碰撞钢套箱的部分,随着船艏行进,挤压并刺穿钢套箱,因此与半椭球体尺寸有关的3 个半径是最重要的外形参数,假定其值均与Hdeck成比例,关系如下:

依据不同尺寸的球鼻部分,将球艏船大致分为大球艏与小球艏两类,以此来讨论球鼻外形的影响因素.图7 所示为两类球鼻艏撞击钢套箱的情形,大、小球鼻除了3 个半径RL、RV、RH有明显差异外,小球鼻艏首柱倾角φ1也大于大球鼻艏首柱倾角φ2.小球鼻艏在碰撞行进过程中,随着位移的持续增大,球鼻以上楔形部分将接触并挤压钢套箱上甲板.这使得简化分析计算分成了两个主要阶段,即球鼻的初始接触碰撞与楔形体参与的后续碰撞.对于大球鼻艏来说,由于钢套箱内、外板间距有限,即使在最大撞深时刻也仅有球鼻部分参与碰撞,表明在碰撞全过程中,楔形部分始终未与钢套箱顶板接触,这也简化了解析计算流程.因此,定义大、小球鼻艏的区别在于其上部楔形体是否会参与到挤压钢套箱的过程中.
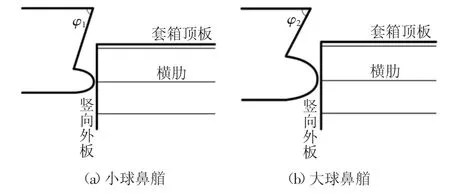
图7 不同尺寸下的球鼻碰撞情形立面示意Fig.7 Schematic diagram of the bulbous bow collision situation under different sizes
假定的楔形艏模型主要参数包括上甲板楔形夹角2θ、船艏高度Hdeck、首柱倾角φ.与球鼻艏模型中球鼻部分的半椭球体水平半径RH类似,对于楔形艏撞击钢套箱场景下,楔形夹角2θ 是至关重要的,2θ值越小,船艏接触到竖桁的位移时刻就会越大,如图8 所示.这也将直接影响到船艏撞击下钢套箱的构件参与数量及损伤面积.

图8 两类船艏碰撞情形平面示意Fig.8 Plane view of collision scenarios of two different bows
2.3 钢套箱被撞位置不同的讨论
钢套箱的组成包括顶板、底板、竖向外板、竖向内板、竖桁与横肋交错组成的纵横舱壁及加劲肋.船艏与钢套箱初始接触位置的不同,可能会导致构件变形区域的改变、参与受力的位移顺序以及提供阻力的构件数量的不同,最终使得钢套箱整体吸能效果有一些差异.例如文献[17]对海上浮式生产储油船(FPSO)遭遇撞击的研究中选取了3 个典型被撞位置,得到了差异较大的撞击力-位移曲线,因此对钢套箱初始受压位置的讨论也很有必要.
针对钢套箱结构的立面构造,给出了如图9 所示的4 种不同点荷载的作用位置:纵横板交界处、横肋中点、竖桁中点、竖桁和横肋组成的舱壁内部某点.初始碰撞位置的不同对钢套箱竖向外板及内部各构件的受力顺序及参与情况会带来一定影响.
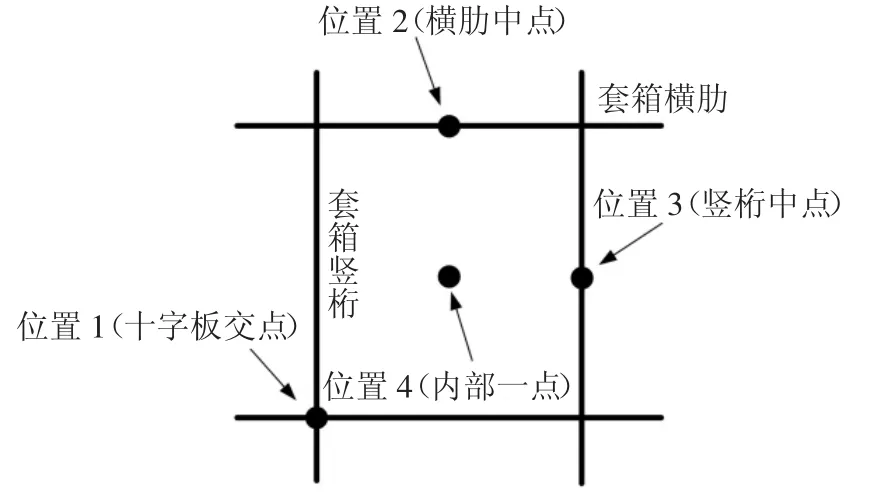
图9 四类撞击点位置示意Fig.9 Four types of impact point positions
一般来说,无论是带球艏船舶亦或是楔形艏船舶,其尖锐的船艏结构,在初始接触的时刻均可视为点荷载.另外,相比于排水量大于10 000 DWT 的船舶舷侧结构,钢套箱纵横舱壁间距较小,这意味着套箱竖向外板由于受到未变形的横肋、竖桁约束,变形区域较小,在较小的撞深下外板就会破裂并进入撕裂模式,采用公式(3)计算外板破裂前变形阻力在一定计算精度范围内是合理的简化.
基本假定中表明各构件以没有发生变形损伤的其他构件作为局部受力破坏的边界.由于受到未变形的纵、横肋约束,对于外板受力而言,不同的撞击点位置会带来不同的初始变形区域,如图10 中阴影区域所示4 个大小不一的矩形面积.在楔形船撞击下的外板破裂前阻力计算中,边界条件取矩形短边的一半,即公式(4)中L1和L2的取值会随着变形区域的不同发生变化.对于破裂位移时刻,后续公式(17)和(18)中l0值不同,也会使得外板破裂进入撕裂模式的临界撞深有所差别.这意味着初始变形区域越大,外板阻力越大,破裂时的临界撞深也越大,参与耗能更多.
同样,不同撞击位置下钢套箱内部构件参与受力的顺序也会不同.例如对于第一类位置,撞深零时刻套箱内部十字板即开始发生变形;对于第二、第三类,首先参与受力的则是单独一道横肋或竖桁;第四类撞击位置发生在内部一点时,直到船艏接触到矩形四个角点才会有交叉十字构件参与受力,这意味着与前三种撞击位置相比,内部构件参与耗能的位移时刻稍滞后,但在后续很短的撞深范围内,会有多个T 形、L 形构件同时或依次发生变形,参与耗能.各构件参与碰撞的情形在2.4 节展开讨论.
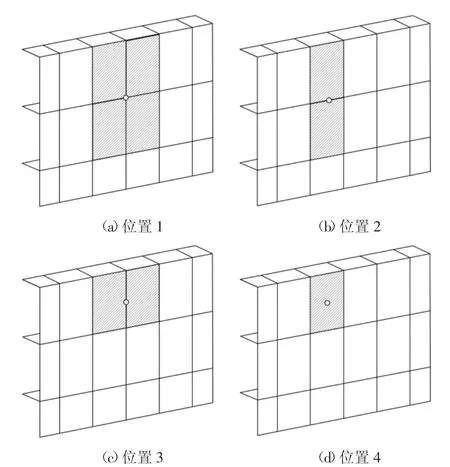
图10 不同撞击位置下的外板初始变形区域Fig.10 Initial deformation area of outer plate at different impact positions
根据上述分析,通过后续精细化有限元技术模拟得到如图11 所示撞击力-撞深曲线,其中横坐标撞深范围为0~0.2 m.从图11 可看出,位置1 下的撞击力因外板变形区域较大和开始时内部十字板构件的参与,初始撞击力斜率最大;位置4 在撞击初始时刻套箱内部构件未参与受力,初始撞击力斜率最小.另外,由于钢套箱内部构件排布密、间距小的特点,撞击点处相邻的构件能很快参与受力,因此当撞深达到0.2 m 时,不同位置下钢套箱撞击力趋于一致,与船舶舷侧结构相比,后续撞击力差别相对较小.
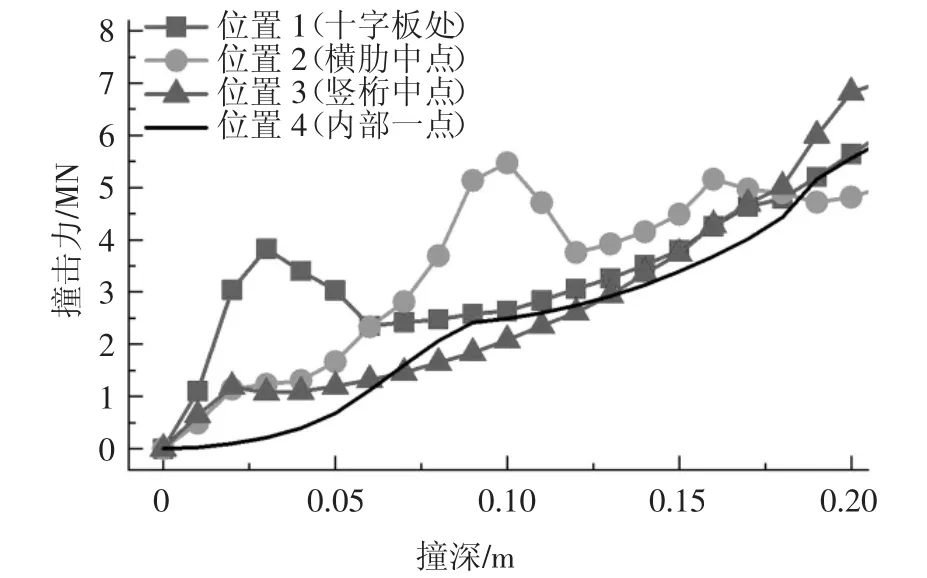
图11 四类位置下撞击力-撞深曲线示意Fig.11 Impact force versus crush depth curves for four types of impact locations
2.4 钢套箱内部构件参与碰撞情况
对于上述4 类钢套箱被撞位置,对其后续的构件碰撞情形讨论在思路上是一致的.因此,选取横肋、纵桁交界处为被撞位置,展开钢套箱内部各构件参与碰撞情况的分析.
以图12 为例,IJ 为钢套箱顶板,图中所示为5道竖桁、2 道横肋、1 道顶板所组成的纵横舱壁结构.在解析计算分析中,力学模型边界条件为距离撞击处最近且未参与碰撞的纵、横肋,即当撞击位置为点O 时,阻力计算过程中模型边界即为四边形ACEG.
对于带球鼻艏船舶来说,假设撞击点为O 点,一旦船艏与钢套箱接触,HD 与BF 所组成的X 形十字板开始变形,如图12(a)所示.当船艏的进一步行进导致HD 与BF 组成的X 形十字板构件压碎后,随着位移的持续增大,球鼻下一步将会接触到点H 和点D.此时,钢套箱内参与受力的构件为由HN、HA、HG构成的T 形构件和与之对称的由DK、DC、DE 构成的T 形纵、横梁组合结构,如图12(b)所示.
对于楔形艏船舶,假设楔形体最先接触到B 点,那么参与受力的为由BA、BC、BO 组成的T 形构件,如图12(c)所示.随着楔形船的进一步前进接触至点O,参与碰撞的为由HO、OD、OF 组成的T 形构件.当碰撞至点A 时,由于AB 在之前的碰撞中参与受力变形,丧失承载能力及边界约束,此时参与碰撞的为由AI、AH 组成的L 形构件,如图12(d)所示.值得一提的是,一般情况下两道竖桁的间距与两道横肋之间的距离有所不同,因此在计算T 形构件阻力时,带球艏船舶与楔形艏船舶撞击场景下公式(11)(12)(13)中参数c 的选取有所不同,需加以区分.
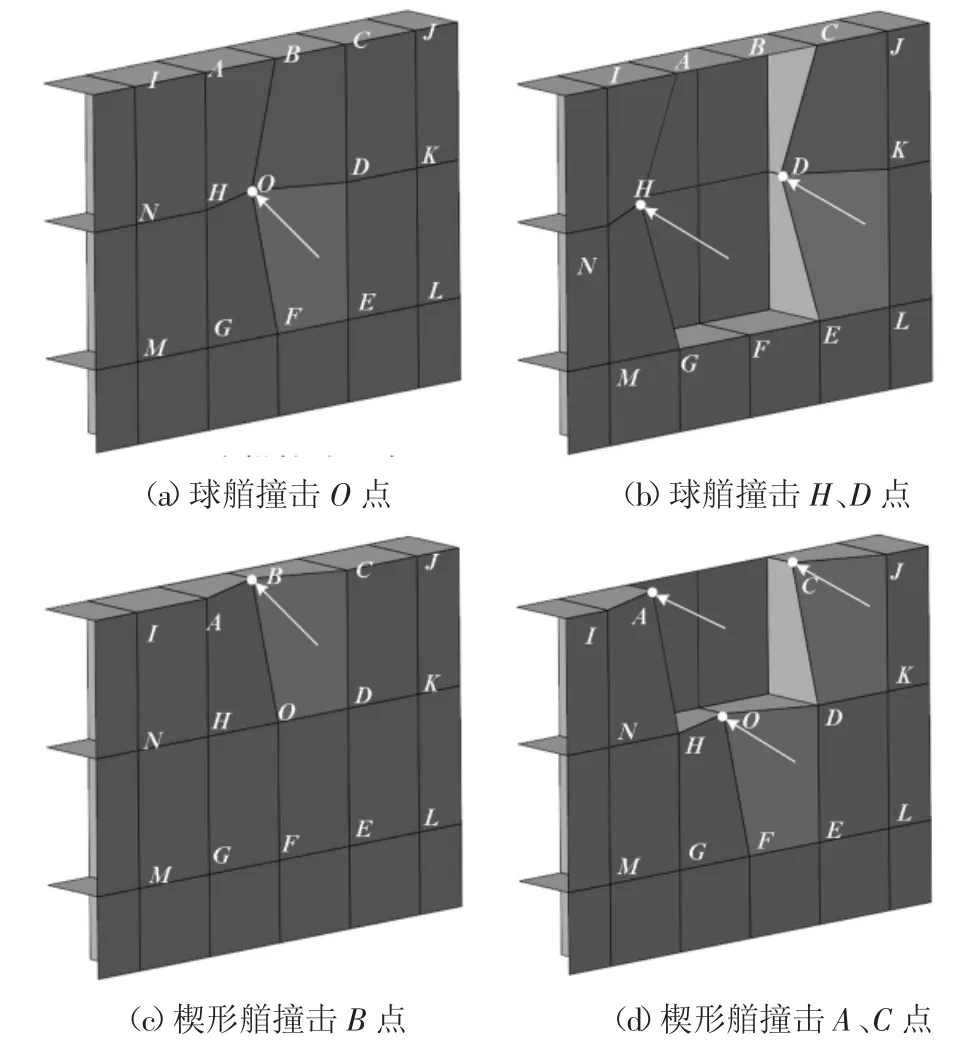
图12 构件参与碰撞情况示意Fig.12 Component participation for different collision scenarios
2.5 构件撕裂临界撞深的确立
对于钢套箱竖向外板,在破裂前后其阻力大为不同,破裂前主要以膜拉伸及弯曲能量耗散的方式抵抗撞击,而破裂后的外板阻力大大降低,视为撕裂变形.因此,找到外板撕裂的临界撞深是合理、准确预测钢套箱抗撞性的重要一步.一般情况下认为,外板变形增大至材料的断裂应变ε0时,视为外板撕裂.图2 为点荷载作用下外板变形示意,其中点画线总长度L0为变形前外板水平方向长度,实线总长度L为撞深Δ 时外板变形后的长度,板的拉伸应变如下:

当ε=ε0时外板破裂,由cos α 与撞深Δ 的几何关系可推出此时的临界撞深为:

在单轴拉伸试验中,低碳钢的断裂应变一般为0.2~0.35.考虑到尺寸效应和材料缺陷,文献[16]提及全尺寸船侧模型中的断裂应变取0.05~0.10.设计者可考虑实际情况,根据设计标准或其他研究中的建议值自行选取,本文取ε0=0.10.
对于肋板、十字板等受力后先折叠再压碎的构件,每道折叠深度为5H0或2H1,若假设一次折叠后板件进入撕裂破坏,则在参与构件较多的情形下,尤其是钢套箱内部结构阻力计算会明显不足.对于十字板构件,通过式(15)可确定十字板在第N0道折叠中构件破碎,整个构件折叠深度为D=(N0-1)×2H1.
2.6 加劲肋的简化计算方法
由于加劲肋不是主要受力构件,其分担阻力的能力有限但也不可忽视,因此采用等效厚度法[24]简化计算加劲肋的阻力,将加劲肋的横截面积均匀分布给外板,便可得到等效厚度如下:

式中:t 为外板自身厚度;A1为加劲肋横截面积;d 为相邻两道加劲肋的间距.
2.7 解析计算方法流程
综合上述研究内容,给出钢套箱抗撞性能研究的解析计算方法,汇总至图13.
3 计算模型介绍
通过选取一般典型构造,建立了简化船艏模型、简化钢套箱模型,以便于确定解析计算方法的普遍适用性.选取精细化的5 000 DWT 球艏船模型和椒江二桥主桥钢套箱模型,采用解析计算方法和数值模拟结果对比,验证适用于钢套箱的解析计算方法在实际工程中的准确性.本节将介绍各船艏和钢套箱尺寸设计、内外部构造及其相应有限元模型.

图13 钢套箱抗撞能力曲线的解析计算方法Fig.13 Flowchart of analytical method to calculate the anti-collision capacity curve of steel fender
3.1 不同外形船艏模型
由文献[11]提出的简化船模设计尺寸,分别建立船艏模型Ⅰ和Ⅱ.如图14 所示,假定球艏船的船艏高度Hdeck=8 m,上甲板楔形夹角的一半θ=17°,首柱倾角φ=63°,球鼻椭球部分RL=2.4 m、RV=1 m、RH=0.4 m.楔形船的船艏高度Hdeck=6.2 m,上甲板楔形夹角的一半θ=30°,首柱倾角φ=74°.
船艏Ⅰ和Ⅱ的有限元模型材料为Q235 钢,密度ρ=7 850 kg/m3,弹性模量E=2.06×105MPa,泊松比ν=0.3,假定船艏外壳为刚体,采用壳单元建立,厚度10 mm.
船艏Ⅲ选取Fan[25]等建立的精细化5 000 DWT球艏船模型,同时假定船艏外板为刚性体,不发生变形损伤,能量耗散均由防撞装置承担.限于篇幅,具体尺寸构造见文献[25].
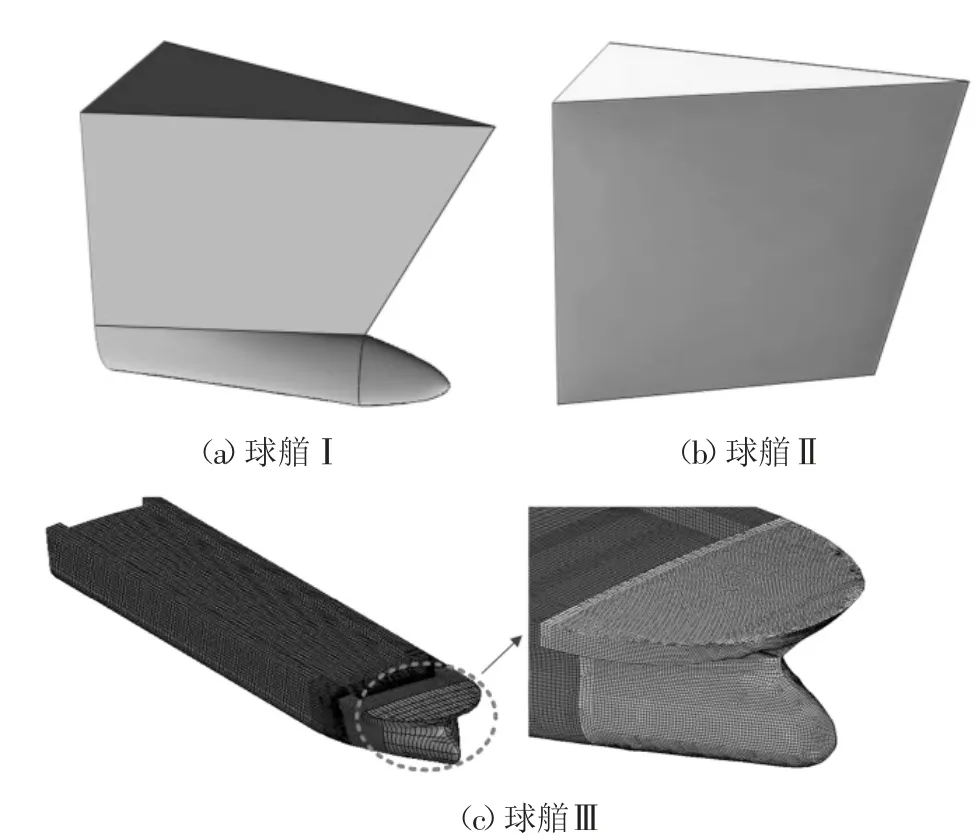
图14 船艏模型Fig.14 FE models of ship bows
3.2 桥梁防撞钢套箱模型
结合钢套箱的基本构造特点,在方柱墩四周建立了如图15 所示的钢套箱Ⅰ.钢套箱Ⅰ构造简易,受力明确,由竖桁、横肋、竖向内外板、顶底板构成.方柱墩墩高26 m,截面尺寸4 m×12 m;承台高6 m,截面尺寸10 m×18 m;钢套箱横肋间距为1.25 m,纵肋间距0.5 m,内、外板间距为2 m.钢套箱Ⅰ的有限元模型采用LS_DYNA 建立,材料为Q235 钢,本构关系为理想线性强化弹塑性力学模型,采用关键字MAT_PLASTIC_KINEMATIC 定义.
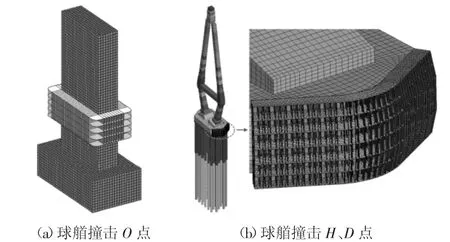
图15 钢套箱模型Fig.15 FE models of steel fenders
考虑到简化分析方法在实际工程中的适用性,钢套箱Ⅱ选取文献[9]建立的用于椒江二桥主塔防撞的精细化防撞钢套箱模型(见图15).钢套箱Ⅱ为固定式钢护舷,由Q235C 钢制成,通过牛腿等构件与主塔承台相连,承台与钢套箱内壁间设置了厚度为10 cm 的橡胶块.套箱主要构件为竖向外板、内板、顶板、底板、横肋、竖桁及加劲肋等,平面呈流线型,外板具有一定弧度,以便于紧贴桥墩;立面为三折线型,套箱宽度从顶板处2 m 逐渐扩大到中部2.5 m,到底部再缩减为2 m.内部横肋间距为1.75 m,竖桁间距为0.6 m 至0.8 m 不等,竖向加劲肋间距分为0.6 m 和1.4 m 两种.钢套箱钢板厚度均为10 mm.其他参数见文献[9].
4 方法验证与讨论
依据已建立好的船艏模型、桥梁防撞钢套箱模型,结合上述讨论采用解析计算方法展开抗撞性分析,并利用有限元模拟结果验证该方法的正确性.拟定如下4 个算例(见表1),各算例均为对中正撞.
算例一、算例二分析了钢套箱Ⅰ在不同外形船艏撞击下的撞击力-撞深曲线关系.算例三、算例四验证了简化分析方法对具有一定弧度的精细化钢套箱Ⅱ抗撞性分析的准确性,确保其在实际工程领域的应用.
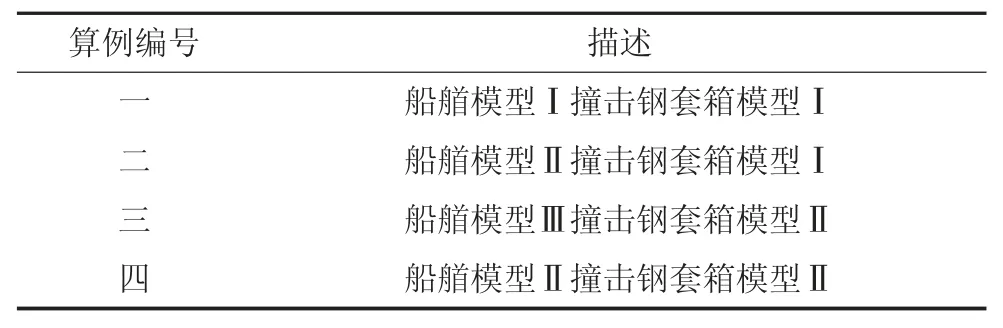
表1 算例汇总Tab.1 Summary of the cases
4.1 算例一
钢套箱模型Ⅰ在船艏模型Ⅰ撞击下,解析计算方法和数值模拟方法得到的力(能量)-撞深曲线如图16 所示.
图16(a)中AB 段为球艏船球鼻开始接触钢套箱,外板和首先接触到的十字板结构参与受力,撞击力在最初一段撞深内迅速升高.外板在B 点发生破裂,承载力大大降低,撞击力迅速降低至C 点.随着船艏的持续前进,球鼻以上楔形部位在D 点接触到套箱顶板,随即顶板和竖桁组成的T 形结构参与受力,撞击力持续增加到E 点.EF 段为竖向外板及T形结构破裂,阻力迅速降低.

图16 算例一结果Fig.16 Result of case 1
对比两种方法计算得到的曲线,可以看到解析计算方法在该工况下吻合较好.
4.2 算例二
钢套箱模型Ⅰ在船艏模型Ⅱ撞击下,解析计算方法和数值模拟方法得到的力(能量)-撞深曲线如图17 所示.图17(a)中AB 段为楔形艏开始接触钢套箱顶板、竖向外板顶部等,阻力持续增大.外板在B 点破裂,承载力降低.当楔形艏行进至C 点处时,竖向第二道十字板结构参与受力.十字板的折叠破碎使得撞击力从D 点开始下降.随着楔形艏撞击深度的进一步增加,钢套箱竖向中心线两端横向范围内各个构件也参与受力.E 点处为横向上的T 形构件参与受力,由于钢套箱的横向对称性,此时共有两道T 形构件进入压碎折叠.F 点为纵向内第三道横肋发生变形,在FG 段内,纵、横向内多个构件依次参与能量耗散,撞击力持续增大.
从图16 和图17 中可以看到,不同船艏对钢套箱阻力的影响较大,楔形艏撞击钢套箱的过程中,参与受力的构件数目多,损伤区域大,钢套箱的阻力随着撞深远远大于球鼻艏撞击下的阻力.对比两种方法,表明了解析计算方法对不同形状船艏撞击下的计算结果均有较高准确度.
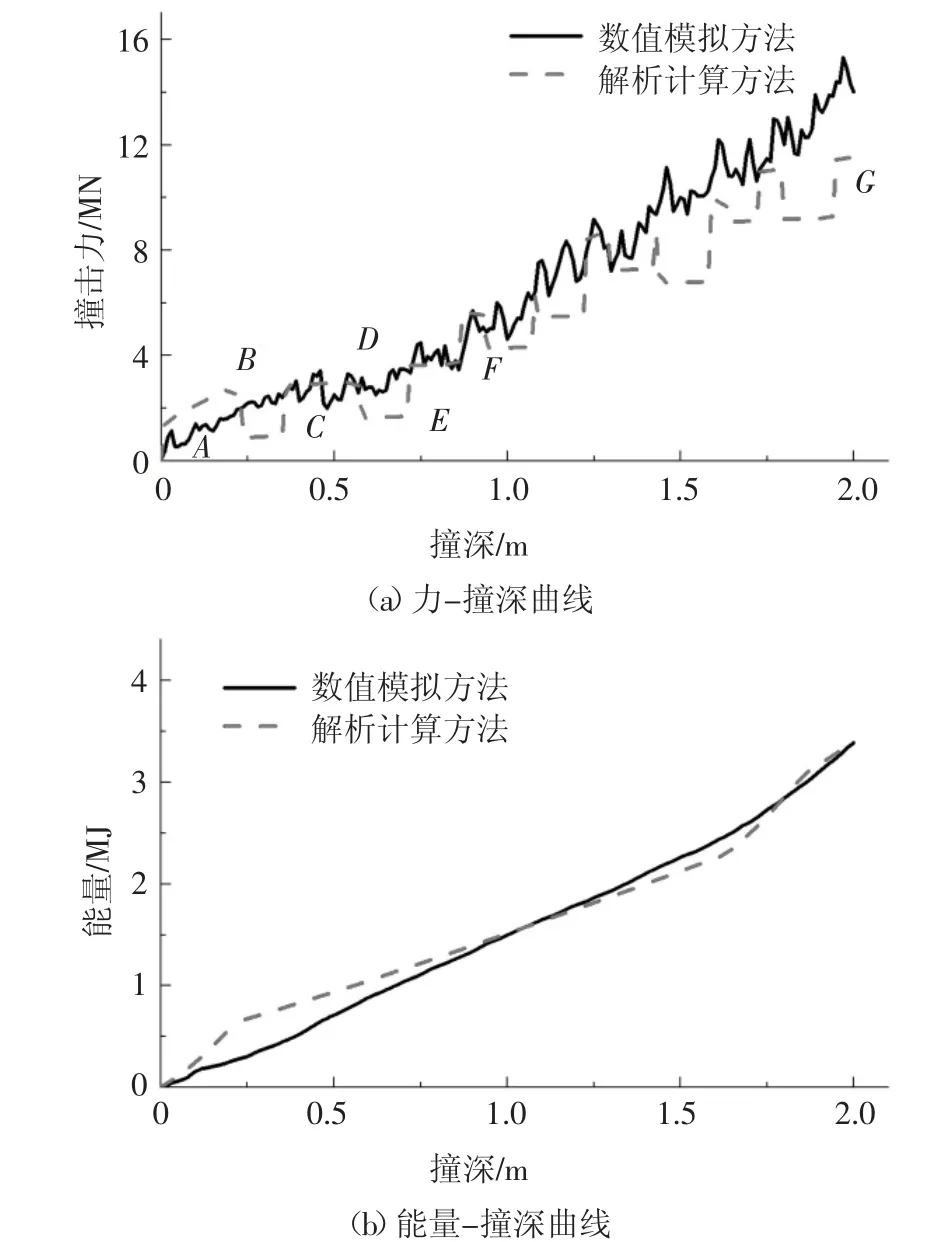
图17 算例二结果Fig.17 Result of case 2
由于实际事故中,船舶速度在撞击过程中会随着能量的耗散降低,其力的时程曲线中,撞击力也会最终归零(卸载为零).本文解析方法、数值模拟均假定船速恒定,为了讨论速度变化对结果的影响,以算例二为基础,开展了船艏在两种不同方式速度设定下的有限元计算,当船艏以3 m/s 的初速度行驶时,力-撞深曲线会在末端进入卸载阶段(由文献[26]可知,在该阶段储存的弹性势能释放,船舶速度方向与初始方向相反),如图18 所示.
对比恒定速度和3 m/s 初速度撞击下,卸载阶段前的力-撞深关系,从图18 中可以看出,两条曲线较好地吻合,撞击力并无较大差异,表明总体上该假设的影响是较为有限的.
另外,本文主要研究钢套箱的耐撞性,钢套箱作为一种吸能结构,主要是吸收船舶动能.根据船舶的质量和速度,可以得到动能的大小,然后依据解析计算方法得到的撞击力-撞深关系,预计撞深大小,得出给定撞深下的峰值力、耗能大小,从而为钢套箱的初步设计提供指导.

图18 两种不同方式的速度设定下撞击力-撞深关系对比Fig.18 Comparison of impact force-crush depth relationship under two different speed settings
4.3 算例三
钢套箱Ⅱ代表了实际工程中所应用的钢套箱,其造型更符合工程实际,外部呈流线型,内部构造也相对复杂,包括加劲肋的布置、竖桁的中空处理等,对钢套箱Ⅱ的计算与验证尤为重要.船艏Ⅲ撞击钢套箱Ⅱ下的解析计算方法和数值模拟方法得到的力(能量)-撞深曲线如图19 所示.整个撞击过程位移为2.4 m,从球鼻接触钢套箱外板开始直到即将接触至套箱内板.根据2.1 节中基本假定,由于在撞击发生后,钢套箱内板紧贴桥墩没有变形空间,因而不考虑内板耗能.图19(a)中B 点为外板破裂时刻位移.其临界撞深大于上节简化模型解析计算中的外板破裂位移,这是由于椒江二桥钢套箱纵横肋间距大于简化的典型钢套箱,在相同的断裂应变下,外板可以有更大的面外位移.D 点即为撞击点横向两道对称十字板参与受力的位移时刻,撞击力快速上升至E点.EF 段的提高主要由于十字板在折叠压碎过程中平均压碎力的贡献.
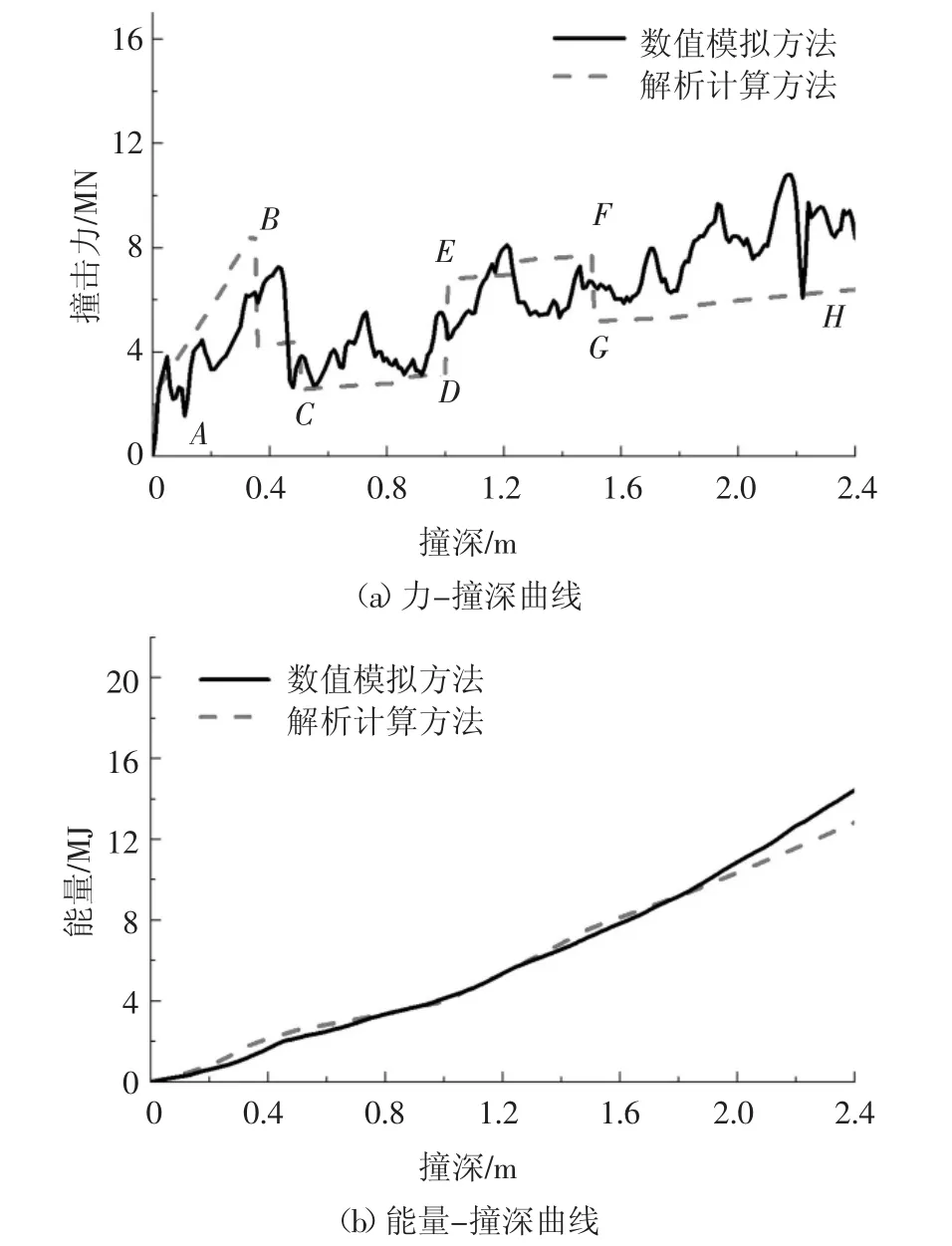
图19 算例三结果Fig.19 Result of case 3
4.4 算例四
由算例一和算例二对比看出球鼻艏和楔形艏撞击下的钢套箱阻力差别,因此算例四计算了楔形艏撞击下钢套箱Ⅱ的阻力,结果如图20 所示.解析计算出的力-位移曲线在发展趋势上与数值模拟结果高度吻合.由于楔形艏撞击下钢套箱内部参与受力的构件数量多,解析计算中忽略了构件间的相互作用,因此略低估了钢套箱的耗能性能,总体而言误差较小,且出于偏安全的考虑,计算结果可以接受.
5 结论
本文提出了适用于桥梁固定式钢套箱能力分析的解析计算方法,给出了详细的计算流程,得到了在给定撞深下力的变化趋势和套箱耗能能力.该方法简单、快速,能有效地分析得到钢套箱的抗撞能力曲线,采用精细有限元分析对计算结果进行了验证,得到主要结论如下:
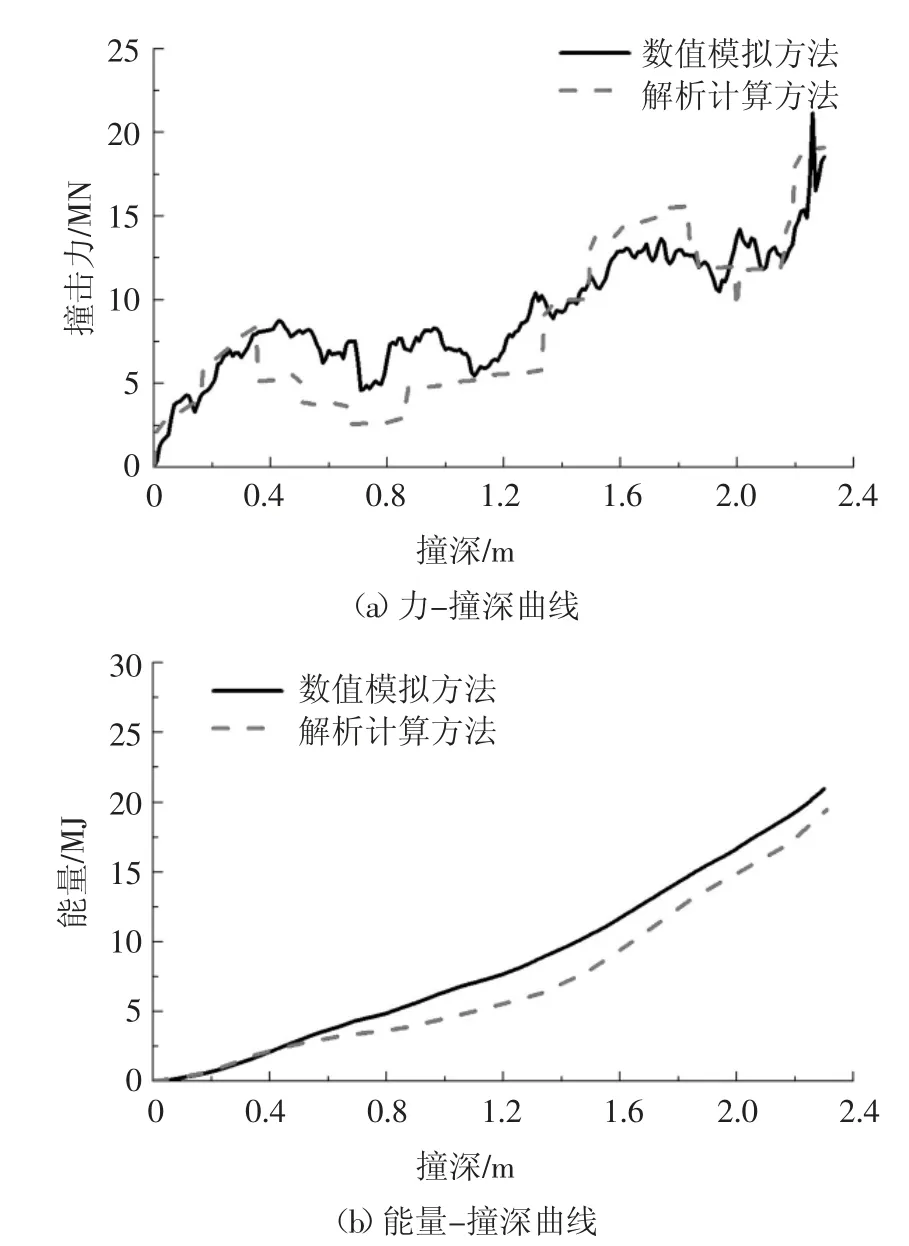
图20 算例四结果Fig.20 Result of case 4
1)采用提出的方法计算得到的撞击力-撞深曲线与数值模拟方法得到的结果较好地吻合,表明了该方法的有效性、适用性.将其运用于桥梁防撞钢套箱初步设计中,将有效提高设计效率.
2)对于带球艏和楔形艏两种类型艏部的船舶,其撞击下的钢套箱阻力存在显著差别.由于楔形艏船对钢套箱的破坏程度更高,结果往往大于带球艏船撞击下的阻力.
3)针对桥梁防撞钢套箱整体尺寸小、内部构件密的构造特点,对不同撞击位置下,初始撞深内板件的变形特征做了较为详细的分析与讨论,分析假定的变形特征与数值模拟结果较好地吻合.
4)解析计算了带有一定弧度的钢套箱碰撞阻力,并利用数值模拟方法对比结果,验证了钢套箱解析计算方法在该类钢套箱分析中的适用性.
本文重点建立了解析计算方法的基本思路,仅进行了有限情况的验证,后续应结合不同类型船舶、不同套箱(如浮式套箱、组合结构套箱)等进一步验证方法的有效性,同时,如何运用其进行设计,有待进一步深入研究.
