基于等参映射与改进折半法的公路车桥耦合分析系统

赵越，黄平明，刘修平，韩万水，毛旺涛

（长安大学 公路学院，陕西 西安 710064）

车桥间的耦合作用不仅会影响到桥梁结构的安全性和适用性，还会影响行车安全和舒适性.近年来，桥梁结构形式的多样化、汽车速度和载重的不断加大使得车桥之间的相互作用愈发复杂和不确定，车桥耦合振动问题受到了国内外学者的广泛关注[1-4].

车桥耦合振动的分析方法主要包括3 种：解析法、试验研究法和数值模拟法[5].解析法虽然是理论推导，比较严谨，但当桥梁几何特征和材料特性有限制条件时，在方程建立过程中不可避免地要对实际条件进行简化，而且有些复杂方程无法得到解析解，所以解析法在实际工程中运用有一定的局限性[6].试验法虽然能客观且综合地反映桥梁在车辆动载作用下的实际工作情况，但由于人力、物力消耗较大且操作难度高，实现起来并不经济.目前数值模拟凭借易实现、低成本等特点已成为车桥耦合振动的主要分析手段.早期的数值模拟法大多是基于Visual C++或Visual Fortran 的自主研发分析系统[7-8]，以自编的程序计算桥梁系统的响应.随着各种大型通用商业有限元分析软件的开发，其前处理模块中，桥梁上、下部结构和附属结构等均可选用不同的单元类型来模拟，在求解过程中也能兼顾结构的几何非线性和材料非线性，以此为基础的各种数值方法[9-13]成为模拟分析车桥耦合振动问题的行之有效的工具.

基于数值方法进行车桥耦合分析系统编制主要包括基于模态叠加法及基于全耦合理论两种[14].相比于后者，模态叠加法简单实用，但结构高阶模态的提取较难，分析结果的精度易受影响[15].基于全耦合方法的车桥耦合分析物理意义明确，分析精度相对较高，但由于车辆对桥梁结构每一时步的加载求解均需借助复杂的迭代过程，故分析效率相对较低，尤其是在分析高流量、高随机车流作用下大跨径桥梁的结构动力响应问题时，将面临较高的时间成本问题[16]，因此提高车桥耦合分析运算效率已成为当前国内外学者的一个研究方向[17].例如张楠等[18]提出了基于全过程迭代的车桥耦合动力分析方法，可通过人为干预促进计算收敛，相比传统的时间步迭代方法，总求解次数大幅减少.李岩等[19]提出了一种维度时变的随机车流与桥梁耦合振动分析方法，使得振动方程单步的求解维度降低，既保持了整体法计算稳定的特点，又有效提高了计算效率.Chen 等[20]则通过将随机车流等效为移动荷载列的方法，达到了降低计算成本的目的.总体来看，车桥耦合分析系统可以从桥梁模型、荷载模型以及计算方法上进行优化.

本文以优化确定车桥接触点的插值系数和加载位置为出发点，引入了四边形等参映射和改进折半查找法提高公路车桥耦合分析系统的计算效率.首先，采用MATLAB 语言建立公路桥梁典型车辆动力分析模型，基于ANSYS 建立桥梁有限元模型；其次，采用全过程迭代法分别求解得到桥梁和车辆的运动状态，通过程序间的接口调用施加车桥间作用力，期间引入四边形等参映射和改进折半查找法并控制时步输出结果以提高车桥耦合运算效率；最后通过经典数值算例和实桥应用对比验证所建立的分析系统的准确性和实用性.

1 基于等参映射与改进折半法的车桥耦合分析系统建立

1.1 车辆模型

汽车车辆一般由车体、车轮等构件以及连接这些构件的减震系统、悬挂系统组成，根据车桥耦合振动分析的需要对车辆模型进行简化，将车辆模拟为刚体的组合，刚体之间通过轴质量块、弹簧元件和阻尼元件相互连接，不同车型所对应的车辆动力分析模型不同.根据课题组前期研究成果，目前公路常见车辆按照车辆轴数、轮数、轴距、轴重等数据可划分为5 大类，17 个车型[21-23].采用MATLAB 语言，针对17 种车型分别建立相应的车辆动力分析模型.

在车辆动力分析模型建立过程中，车辆被划分为不同的刚体部件，如车体、车轮等.空间内单一刚体具有3 个方向的平动和3 个方向的转动自由度.在车辆匀速直线前进时，刚体部件沿着车辆前进方向的振动对桥梁的竖向及横向振动影响不大，因此各刚体沿车体运动方向的自由度可忽略，此时车体具有5 个自由度：竖向、横向、点头、侧滚和摇头，每个车轮具有横向和竖向2 个自由度，拖挂式车型不考虑横移和摇头这2 个自由度，每个车体具有浮沉、点头及侧滚3 个自由度，每个车轮只有竖移一个自由度.

图1 以三轴车（双后轴）为例，给出了相应的动力分析模型立面及侧面图.其中分别表示第i个轴的弹簧刚度和阻尼，i=1、2、3，j=vuL、yuL、vlL、ylL，表示第i 个轴的竖向和侧向对应的上层和下层位置，Zvr、Yvr、θvr、φvr、φvr分别表示车体的竖向、横向、点头、侧滚和摇头位移.Li表示第i 个轴距离车体质心处的长度,分别表示第i 个轴左、右轮的竖向位移，分别表示第i 个轴左、右轮位置处的路面粗糙度和桥面处的竖向位移.

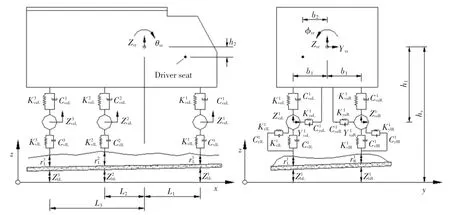
图1 三轴车动力分析模型Fig.1 Dynamic analysis model of three axle vehicle

1.2 车桥运动方程及求解策略

车桥耦合系统的动力方程可表示为：

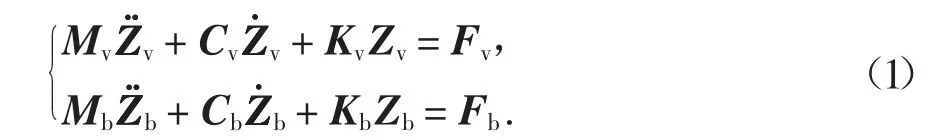
式中：Mv、Cv、Kv分别为车辆系统的总体质量矩阵、总体阻尼矩阵及总体刚度矩阵；Mb、Cb、Kb分别为桥梁系统的总体质量矩阵、总体阻尼矩阵及总体刚度矩阵；Zv、Zb分别为车辆、桥梁系统的位移向量；Fv、Fb分别为车辆、桥梁系统的荷载向量.

在车辆运行过程中，假设车轮始终与桥面接触，桥梁振动引起的桥梁竖向位移将引起车辆减震系统、悬挂系统的变形，且路面粗糙度也是车桥耦合体系的主要激励源之一，因此车桥系统之间的相互作用力既是车辆和桥梁系统运动状态Zv、Zb的函数，也是路面粗糙度Ra的函数，则车桥耦合系统的运动方程可进一步表示为：

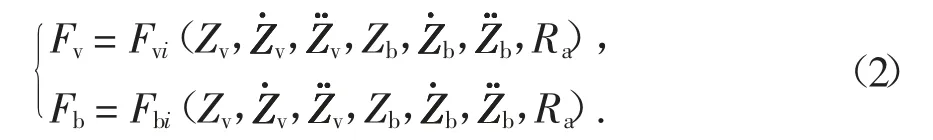
联立式（1）与（2），对车辆与桥梁两个子系统建立耦合关系.采用全过程迭代法分别求解桥梁子系统和车辆子系统，主要迭代过程通过MATLAB 编制相应运算程序予以实现，期间由基于ANSYS 的桥梁有限元模型及相应分析过程提供响应输出，具体流程如图2 所示，收敛准则定义为＜0.1.全过程迭代法每一步均为全时程计算，具有思路清晰明确、易于操作、计算准确、占用内存少等优点.

1.3 基于等参映射的接触点荷载分配

目前桥梁结构桥面模拟有限元模型多为梁格模型、实体或板壳单元模型，车轮荷载一般简化为集中力并分配至相邻4 个节点，如图3 所示.在二维平面内四边形荷载分担方式与位移插值函数一致.当车轮荷载作用于某一位置（x，y）时，相应的等参映射关系如图4 所示.

坐标映射关系为：

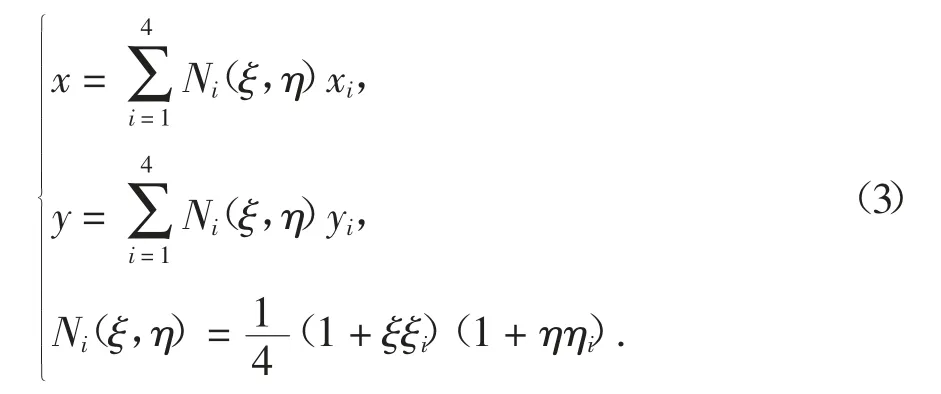
式中：x、y 是车轮荷载与桥面接触点坐标；xi、yi分别为四边形单元的第i 个节点的横、纵位置；ξ、η 为x、y映射到母单元的值；ξi、ηi分别为母单元的第i 个节点的横、纵位置，是已知量；N（iξ，η）为等参映射点（ξ，η）的函数[24]；函数值Ni为四边形单元的第i 个节点的荷载分配系数.

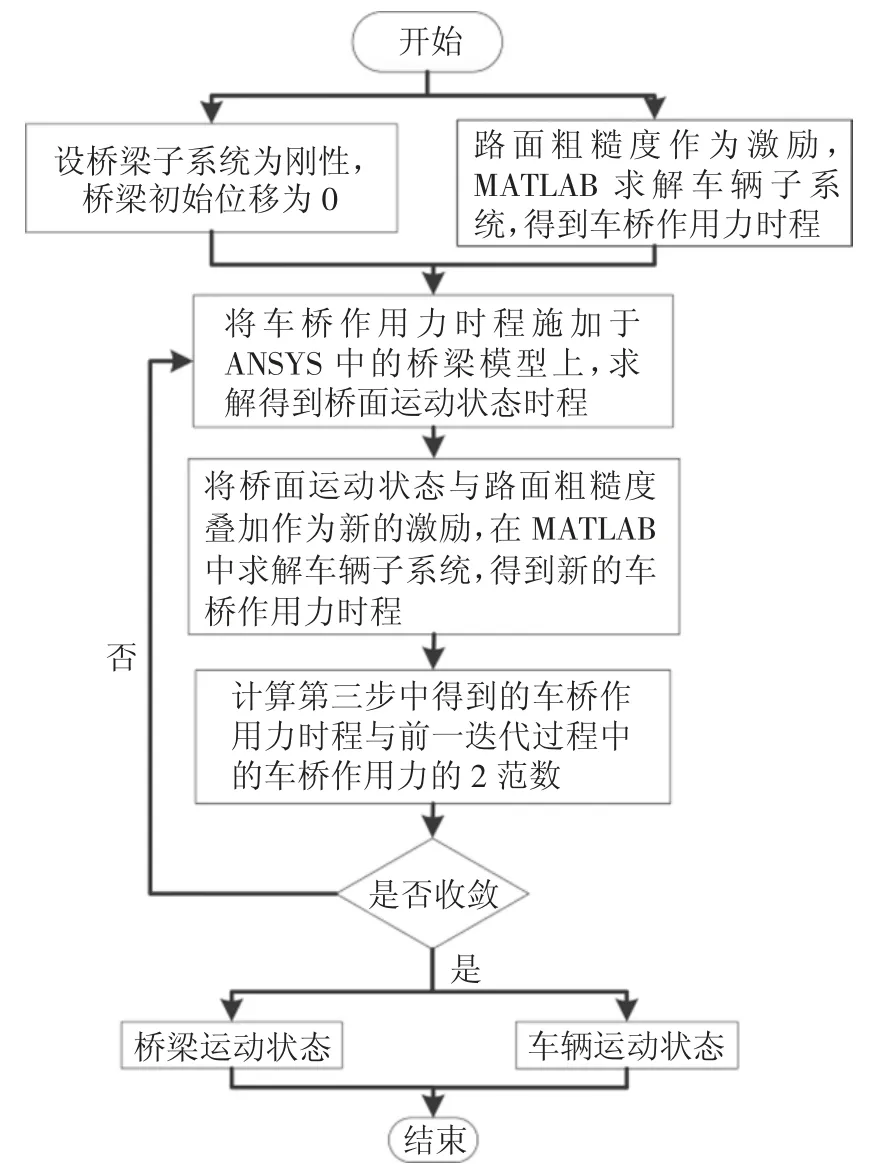
图2 全过程迭代法流程Fig.2 Inter-history iteration flow chart

图3 接触点荷载分配Fig.3 Distribution of contact point load

图4 等参映射Fig.4 Isoparametric mapping

双线性方程组（3）的未知量ξ 和η 可通过牛顿迭代法[25]求解，进而计算出分配系数Ni，实现车轮荷载的自动加载.迭代过程为：

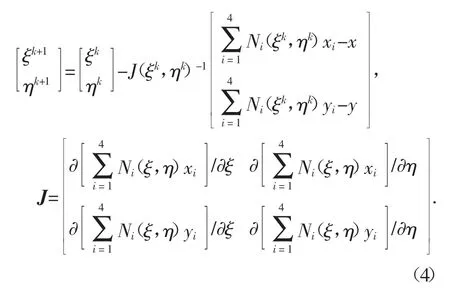
式中：J 为雅克比矩阵；ξk、ηk分别为第k 次迭代的计算值.当时，则停止迭代，迭代误差ε取值10-8.

1.4 基于改进折半法的快速加载

为实现车轮荷载的快速自动加载，需定位临近4个节点的位置信息，折半查找法作为一种在有序数组中查找某一特定元素的搜索算法，通过不断将查找范围减半提高搜索效率，本文将折半法查找确定值的思想扩展到查找车轮作用区间范围上.折半查找的前提条件是必须将搜索目标范围排成有序数列，虽然折半查找效率高，但排序本身又增加了一定工作量.桥梁结构模型的特点决定了同一计算过程中，主梁节点一经确定便不再改动，因此全部计算过程仅需一次排序，后续所有车轮作用范围的确定均可直接使用，从全局角度考虑可有效提高查找效率.

以车轮纵向加载点x 处的临近坐标定位为例，横向加载点y 处临近点查找与之类似，查找流程如图5 所示，具体步骤如下：

1）导入ANSYS 模型中待求车辆所在车道上全部单元的节点坐标，按照升序排列形成一维矩阵t.

2）初始化：计算一维矩阵的大小确定last，令front=1.

3）计算mid=round（（front+last）/2），round 表示四舍五入.

4）如果mid=last，那么查找结束，车轮x 处于一维矩阵t 的上限位置是mid，下限位置是mid-1.否则，判断车轮x 的值是否介于一维矩阵t 的front 和mid 位置之中，若是，则令last=mid，否则令front=mid.

5）继续步骤3），直到mid=last.

确定车轮荷载作用点的临近4 个节点后，通过牛顿迭代法求解方程（3），继而可得到每个节点处的插值系数，从而确定荷载分配值.为减少车桥耦合计算工作量和提高程序运行效率，仅将荷载作用点的位移和速度输出，利用已知的插值系数计算出车轮处的速度和位移，用于车桥作用力的求解中.

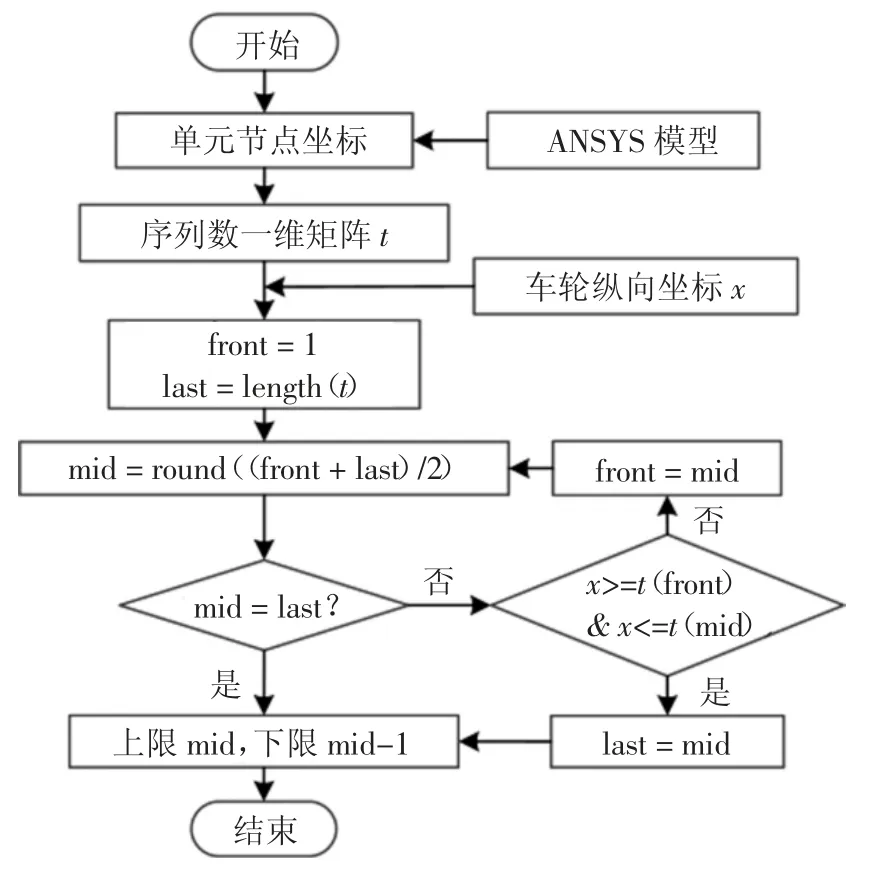
图5 改进折半查找法流程Fig.5 Improved half search algorithm flow

2 数值算例验证

为初步验证本文建立的车桥耦合分析系统的准确性，首先基于数值分析算例进行对比.由于复杂桥梁的数值分析结果较难得到，故以经典的单自由度弹簧-质量模型通过简支梁桥为例，将所建立系统分析结果与文献[26-27]分析结果进行比较.算例信息如图6 所示，简支梁全长25 m，桥梁有限元模型由100 个BEAM4 单元组成.截面惯性距2.9 m4，弹性模量2.87×109kN/m2，线密度2 303×103kg/m，泊松比0.2，车辆质量5.75 t，弹簧刚度1 595×103N/m，移动速度v=27.78 m/s，不考虑阻尼和路面不平整度.

图6 单自由度车辆通过简支梁桥模型Fig.6 Vehicle of single degree of freedom passing through simply supported beam

桥梁基频有限元计算值4.779 Hz，理论值4.78 Hz，二者非常接近.桥梁的跨中挠度时程曲线及车辆竖向位移时程曲线如图7 和图8 所示，车辆竖向加速度时程曲线如图9 所示，车桥接触力时程曲线如图10 所示.根据结果可知，采用本文方法计算的曲线与文献[26-27]中的曲线吻合良好.车辆竖向加速度时程曲线与车桥接触力时程曲线变化趋势相同，初步说明所建立分析系统的分析精度满足基本要求.

图7 桥梁跨中挠度时程曲线Fig.7 Deflection time history curve of bridge mid-span

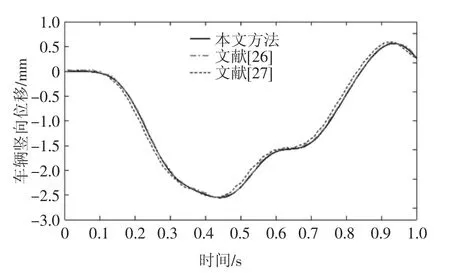
图8 车辆竖向位移时程曲线Fig.8 Vertical displacement time history curve of vehicle

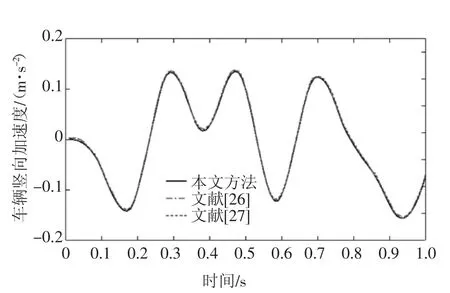
图9 车辆竖向加速度时程曲线Fig.9 Vertical acceleration time history curve of vehicle

图10 车桥接触力时程曲线Fig.10 Vehicle-bridge contact force time history curve

3 实桥验证与应用

3.1 桥梁信息

四渡河大桥是沪蓉国道主干线湖北宜昌至恩施高速公路的控制性工程，是一座主跨900 m 的钢桁梁悬索桥.主梁总宽度为26.0 m，桥面净宽为24.5 m，采用双向四车道布置，单向2.41%纵坡.加劲梁由主桁架、上下平联、横向桁架组成，主桁架采用华伦式钢桁加劲梁.为了减小主梁与主缆相对运动导致的吊杆弯曲应力，桥梁的跨中位置设置刚性中央扣以减弱单向纵坡带来的影响.桥梁信息如图11 所示.

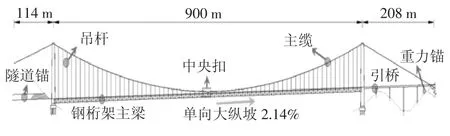
图11 四渡河大桥侧面（单位：m）Fig.11 Side view of Siduhe bridge（unit：m）

基于梁格理论采用ANSYS 建立该桥梁有限元模型，模型建立过程中，将车道所处的桥面等效为4 根纵梁，纵梁、弦杆、腹杆等用BEAM4 单元模拟，主缆、吊索用LINK10 单元模拟.为保证模型的准确性，已根据模态实测数据对初始有限元模型进行了修正[28].根据已有研究成果，新建高速公路桥梁桥面不平整度基本为ISO 标准中的A 级路面[29-30].因此，根据相关标准参数生成如图12 所示的路面不平整度.

图12 路面不平整度Fig.12 Road surface roughness

3.2 基于实测数据的分析系统验证

进一步采用该桥梁对所建立的分析系统开展验证工作，首先设置车辆过桥测试工况，具体工况信息包括：1）两辆三轴卡车以20 km/h 车速匀速过桥；2）两辆三轴卡车以50 km/h 车速匀速过桥.测试工况中车辆行驶位置及动应变测点如图13 所示，动应变测点布设于中央扣处主桁上弦杆上.两辆三轴车所对应的车辆动力模型参数及质量参数如表1 所示[31].

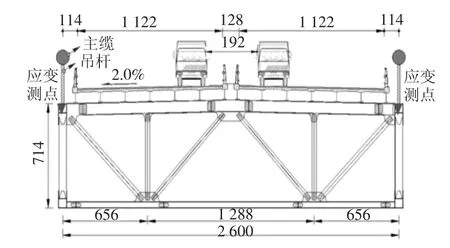
图13 行车试验示意图（单位：cm）Fig.13 Diagram of running test（unit：cm）

表1 车辆技术参数Tab.1 Vehicle technical parameters

采用基于等参映射与改进折半法所建立的车桥耦合分析系统对上述两个测试工况进行分析，并提取与测点位置相应单元的应变信息，实测结果与理论分析结果的对比如图14、图15 所示.由图14 和图15 可知，基于所建立车桥耦合分析系统所得到的分析结果能够与实测结果良好地吻合，20 km/h 和50 km/h 车速下跨中应变峰值误差分别为1.3%和0.31%，说明所建立的车桥耦合分析系统分析精度能够满足要求.应变峰值出现误差不同的主要原因在于行车试验有一定的随机性，车桥耦合分析计算中将试验车辆车速确定为一个定值，但实际车辆难以精确保持在预定车速，并且车辆在桥上的运行位置亦会产生轻微的变化，对结构的振动响应产生影响，因此导致出现应变峰值误差不同的情况.

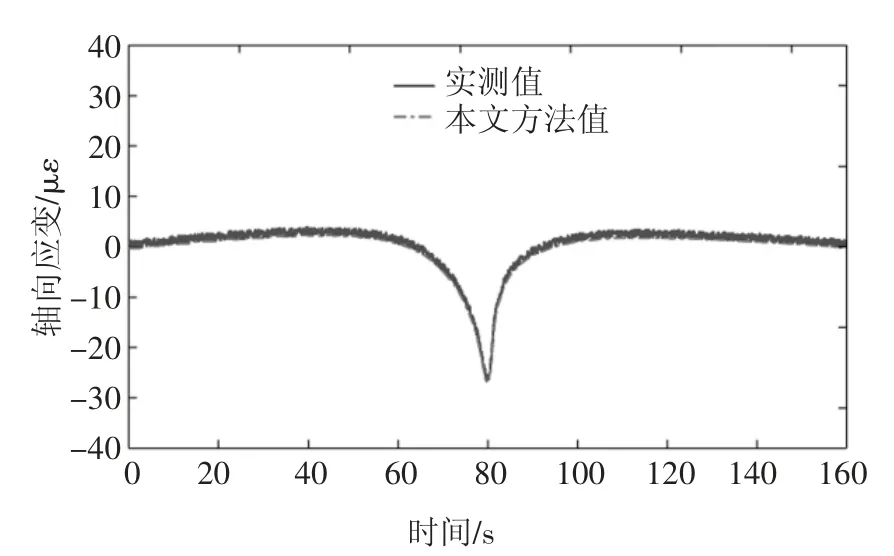
图14 20 km/h 车速下动应变曲线Fig.14 Dynamic strain under 20 km/h

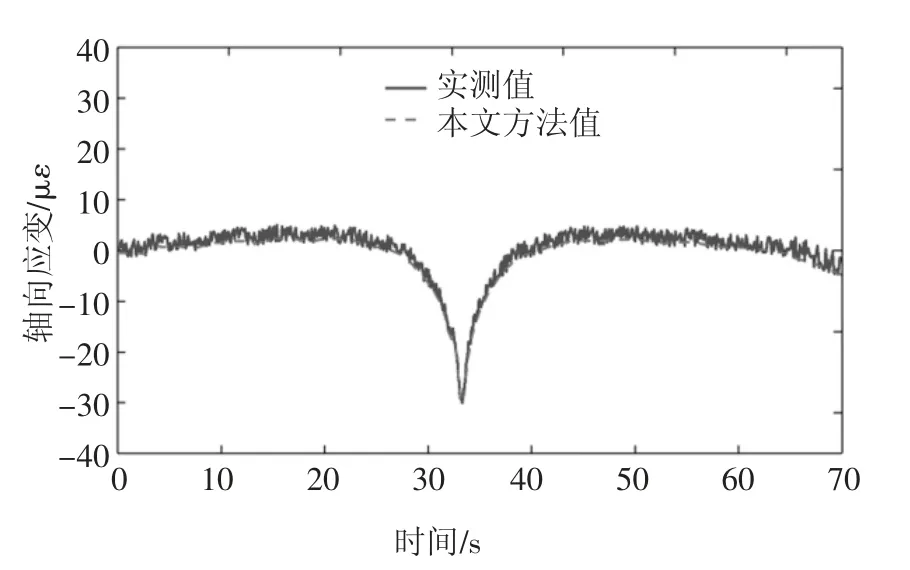
图15 50 km/h 车速下动应变曲线Fig.15 Dynamic strain under 50 km/h

3.3 计算效率分析

图16 给出了本文所建立分析系统在上述2 个测试工况下的迭代进程，可见，尽管2 种车速下所建立分析系统在初始阶段迭代收敛误差很大，但经过3 次迭代后迅速下降，能够在第6 次迭代后达到收敛状态.为进一步分析该分析系统在求解过程中对分析效率的提升情况，现针对算例采用基于时间步迭代的传统分析方法与本文分析方法进行对比，计算2 辆卡车以60 km/h 车速双车并行工况下结构的响应.由于本文所提出方法优势在于占用系统计算资源少，为体现本文方法相比传统方法提升效果，选取在相同计算机配置情况下2 种方法计算时长作为体现计算效率的指标.全部计算采用常规办公用计算机，主要配置为处理器6 核6 线程，主频2.8 GHz，内存8 GB.

首先对比两种方法所得到的桥梁跨中竖向加速度和位移响应，如图17 所示.可知基于时间步迭代的传统分析方法与本文方法所得结果基本相同.加速度及位移变化趋势基本一致，峰值相对误差分别为0.1%和0.22%.

图16 不同车速下迭代次数Fig.16 Number of iterations under different speeds

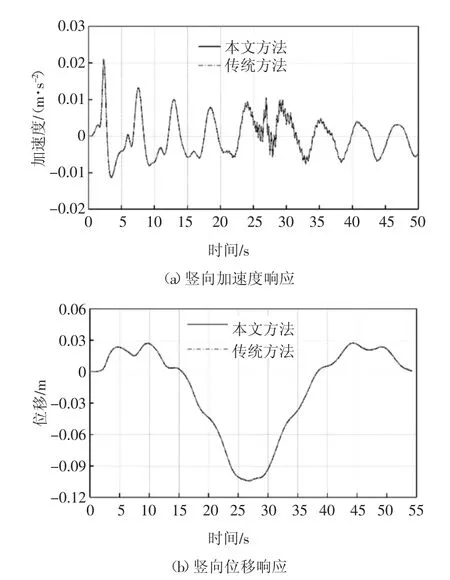
图17 跨中动力响应比较Fig.17 Comparison of mid-span dynamic responses

表2 给出了两种分析方法计算耗时信息.可见两种方法总时间步均为543，总迭代次数相仿，但本文方法通过结合全过程迭代，引入等参映射及改进折半法，实现了车轮作用点临近节点快速定位及自动加载，在保证计算精度的同时，较传统方法求解总耗时减少了42.5%.尽管对于当前目标结构，计算总耗时并不很长，但该分析方法对于进一步进行高强度随机车流下桥梁结构空间动力响应分析具有积极意义，可有效减少高流量及高随机车辆荷载作用时的计算耗时，有较高的计算效率.

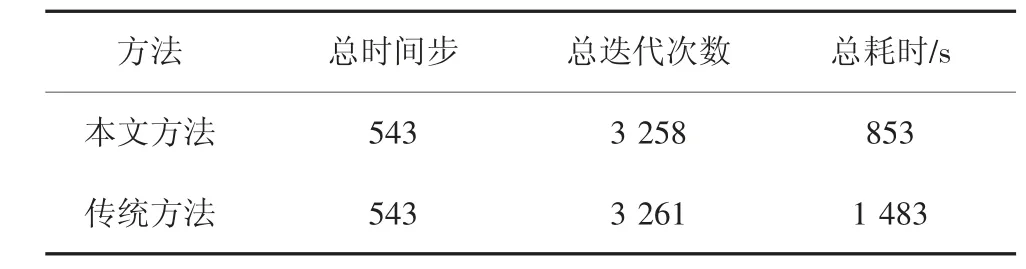
表2 计算效率对比Tab.2 Comparison of computational efficiency

4 结论

针对基于传统全耦合理论开展公路车桥耦合分析效率偏低的问题，在车桥耦合分析系统建立过程中引入等参映射进行荷载分配，利用改进折半法实现车轮荷载快速加载.借助弹簧-质量模型通过简支梁的数值算例对所建立分析系统的准确性进行了初步验证，根据特定测试工况下的实桥响应对所建立分析系统的准确性作了进一步验证，并对分析过程中的迭代进程、分析耗时等问题与传统分析方法进行了对比，得到以下结论：

1）数值算例验证结果显示，基于所建立的分析系统所得到的分析结果与经典数值分析结果基本一致，初步说明引入等参映射及改进折半法建立公路车桥耦合分析系统的可行性.

2）四渡河大桥2 个测试工况实测与仿真结果对比显示，20 km/h 和50 km/h 车速下跨中应变峰值误差分别为1.3%和0.31%.所建立车桥耦合分析系统收敛速度较快，且得到的分析结果能够与实测结果良好地吻合，进一步验证了所建立的公路车桥耦合分析系统的准确性.

3）依托工程实例将所提出的分析方法与传统分析方法进行比较，分析结果显示本文所提出方法相比传统方法计算结果基本保持一致，计算耗时明显减少，具有较高的计算效率，对后续高强度高随机车流下的公路车桥耦合分析具有很好的应用价值.