冷弯薄壁型钢拼合箱形截面短柱承载力叠加法

周天华，李艳春，吴函恒，桑刘睿，张蕾

（长安大学 建筑工程学院，陕西 西安 710061）

由C 形和U 形冷弯薄壁型钢（CFS）基本构件通过自攻螺钉连接而成的CFS 拼合箱形截面在冷弯薄壁型钢结构住宅体系中运用越来越广泛.该类复杂截面形式立柱作为CFS 结构住宅体系的主要承重构件，常被用于门窗洞口和墙体边角等需加强的地方.

国内外相关研究人员对该类截面构件的结构性能进行了研究.袁涛涛[1]和聂少锋等[2]对CFS 双肢拼合箱形轴压柱的破坏模式及承载力性能进行试验研究，结果表明，CFS 拼合箱形截面柱存在局部屈曲、整体失稳等屈曲模式，并通过对比单肢与拼合构件承载力，验证了1+1>2 的拼合效应.然而，拼合截面构件的结构性能易受连接方式的影响，故有学者对拼合截面构件在不同螺钉布置下的受力性能进行了试验和数值研究[3]，提出拼合截面构件的设计准则，提高了预测强度的准确性.赵阳等[4]通过有限元分析总结出不同螺钉间距对CFS 拼合箱形截面承载力性能的影响规律.Zhang 等[5-6]对由∑形截面组成的拼合箱形柱进行试验和有限元研究，并依据试验和有限元结果提出了适用于该截面的承载力计算方法.在研究新方法的基础上，Kherbouche 等[7]对冷弯薄壁型钢组合柱在均布荷载作用下的受力性能进行了数值研究，并提出了基于直接强度法（DSM）的新方法.

Young[8]对由两腹板加劲的槽形截面组成的箱形截面构件进行了研究，但这种截面板易发生畸变屈曲，降低了构件承载力.Dewolf 等[9]对由两个槽形截面组合而成的抱合箱形截面构件展开研究，结果表明较大的腹板宽厚比容易导致构件发生局部屈曲，从而降低了构件的承载力.由C 形截面拼合而成的拼合构件的承载力性能及计算方法也被展开研究[10-11]，但结果对比表明，这种计算方法偏于保守.因此，目前不论是中国规范GB 50018—2002[12]还是美国规范AISI[13]均没有一套计算由基本构件C 形和U形截面型钢经自攻螺钉拼合而成的CFS 拼合箱形截面构件极限承载力的公式.

鉴于此，本文对由1 根C 形截面和1 根U 形截面型钢组合而成的箱形截面构件承载力进行试验、有限元及理论研究.基于中国规范GB 50018—2002和美国规范中的有效宽度法（EWM）及直接强度法（DSM）计算结果的对比，本文提出了一套适用于拼合箱形截面短柱的承载力计算方法——承载力叠加法，以解决目前没有一套能够准确计算该拼合截面构件承载力设计方法的问题，并推进冷弯薄壁型钢在我国的应用.

1 试验概况

1.1 试件设计

试验主要研究了冷弯薄壁型钢（CFS）局部屈曲的箱形截面短柱，试件分为两个系列：120 系列：C122×52×17×1.2、U125×52×1.2；140 系列：C142×52×22×1.2、U145×52×1.2，构件基本尺寸如图1（a）和（b）所示.拼合截面形式如图2 所示.试件板材厚度均为1.2 mm，长度均取3 倍腹板高度.试件均使用ST4.8级平头自攻自钻螺钉连接而成.本文在设计螺钉纵距时，以C 形基本构件截面局部屈曲半波长（λ）c为基准.120 系列构件的纵向螺钉间距分别取45 mm、90 mm 和150 mm；140 系列构件的纵向螺钉间距分别取50 mm、100 mm 和150 mm.

图1 构件截面形式及尺寸Fig.1 Section form and dimension of components

图2 CFS 拼合箱形截面Fig.2 CFS built-up box section

1.2 材料性能

钢材等级为S280.按照《金属材料 拉伸试验第1 部分：室温试验方法》（GB/T 228.1—2010）[14]的有关规定确定试件的截面形状和尺寸.每组设计3个重复试件（T1.2-1、T1.2-2、T1.2-3）.T1.2 表示厚度为1.2 mm，数字1、2、3 指重复的试件编号.试件的实际测量力学性能见表1.

表1 钢材力学性能Tab.1 Mechanical properties of steel

1.3 试验装置及测点布置

1.3.1 试验装置

采用WAW31000W 电液伺服万能试验机（50 t）施加轴向荷载，通过DH3820 高速静态应变测试系统采集应变片和位移计的数据.边界条件为两端固结，利用万能试验机可移动夹头调整试件与加载装置之间的距离，并利用底部球铰圆盘自动找平以确保轴向加载.试验装置及实物如图3 所示.

图3 加载装置Fig.3 Loading device

1.3.2 测点布置

为更准确地捕捉试件的屈曲临界荷载，沿试件纵向跨中及距离跨中正负100 mm（100 mm 约等于C形基本截面的半波长）处布置了应变片.此外，位移计D1～D4 布置在跨中位置，D5 布置在底部端板上，如图4 所示.

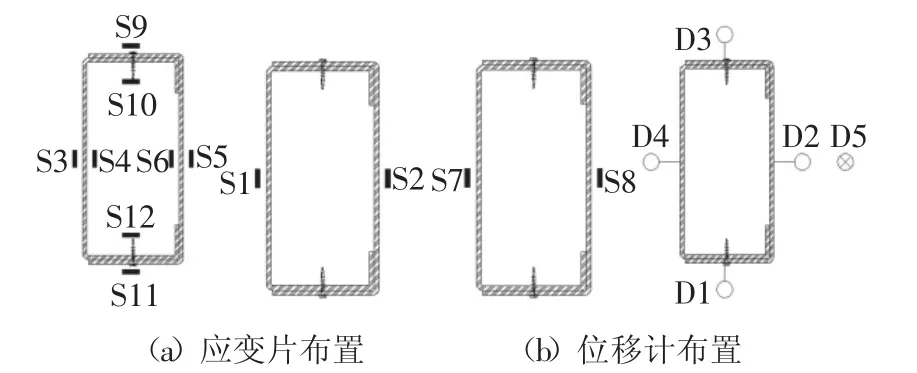
图4 测点布置Fig.4 Layout of measuring points

2 试验结果分析

2.1 试验现象

1）C3-120 截面

C3-120-45-A（试件编号规则如图5 所示）系列试件破坏特征：A1、A2 试件均在荷载加载至52 kN左右时，发生局部屈曲，A3 试件出现局部屈曲现象时，荷载为47.65 kN.三者均是C 形截面构件的腹板先发生内凹，U 形构件的翼缘在相应位置外张.继续加载，屈曲现象越来越明显，直至最终发生局部弯折破坏.具体见图6 和表2.

C3-120-90-A 系列试件破坏过程与C3-120-45-A 系列试件基本一致，A1、A2 和A3 试件发生局部屈曲时的荷载分别为56.21 kN、54.16 kN 和56.19 kN，最终也是局部受压屈曲破坏.具体见图7 和表2.

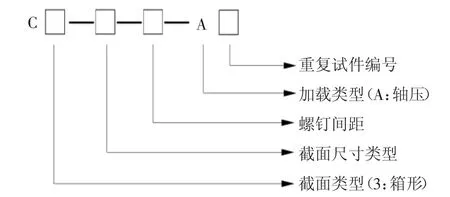
图5 试件编号规则Fig.5 Numbering rules of specimen

图6 C3-120-45-A 系列试件破坏形式Fig.6 Failure modes of C3-120-45-A specimens

图7 C3-120-90-A 系列试件破坏形式Fig.7 Failure modes of C3-120-90-A specimens

C3-120-150-A 系列中A1 试件当荷载加载至52.37 kN 时，试件开始发生局部屈曲，左右翼缘中部外张明显.达到极限荷载时，C 形构件腹板中部出现较为明显的内凹现象.A2 试件加载至54.54 kN 时，U 形构件左翼缘中部开始外张.A3 试件发生局部屈曲时荷载为50.71 kN，此时试件左右翼缘中部发生外张.由此可知，本组试件最终均发生局部弯折破坏，见图8 和表2.

2）C3-140 截面

C3-140-50-A 系列A1、A2、A3 试件发生局部屈曲时对应的荷载分别为39.44 kN、38.15 kN、32.32 kN.最终破坏特征均为局部屈曲弯折破坏，其中A1试件破坏位置靠近中部，A2 和A3 受焊接残余应力影响较大，最终破坏位置靠近端板处，见图9 和表2.

图8 C3-120-150-A 系列试件破坏形式Fig.8 Failure modes of C3-120-150-A specimens

图9 C3-140-50-A 系列试件破坏形式Fig.9 Failure modes of C3-140-50-A specimens

C3-140-100-A 系列中A1 试件当荷载加载至33.14 kN 时，试件开始发生局部屈曲，随着荷载的增大，左右翼缘下端外张现象明显.A2 试件在荷载加载至44.65 kN 时，U 形构件左翼缘的中部开始外张，试件屈曲.A3 试件发生局部屈曲时荷载为40.16 kN.试件最终破坏特征也是局部弯折破坏，见图10和表2.

图10 C3-140-100-A 系列试件破坏形式Fig.10 Failure modes of C3-140-100-A specimens

C3-140-150-A 系列试件破坏过程和C3-140-100-A 系列试件基本一致，A1、A2 和A3 试件发生局部屈曲时的荷载分别为43.33 kN、46.25 kN 和47.47 kN，最终破坏也是局部受压屈曲破坏.具体破坏位置及破坏形式见图11 和表2.

图11 C3-140-150-A 系列试件破坏形式Fig.11 Failure modes of C3-140-150-A specimens

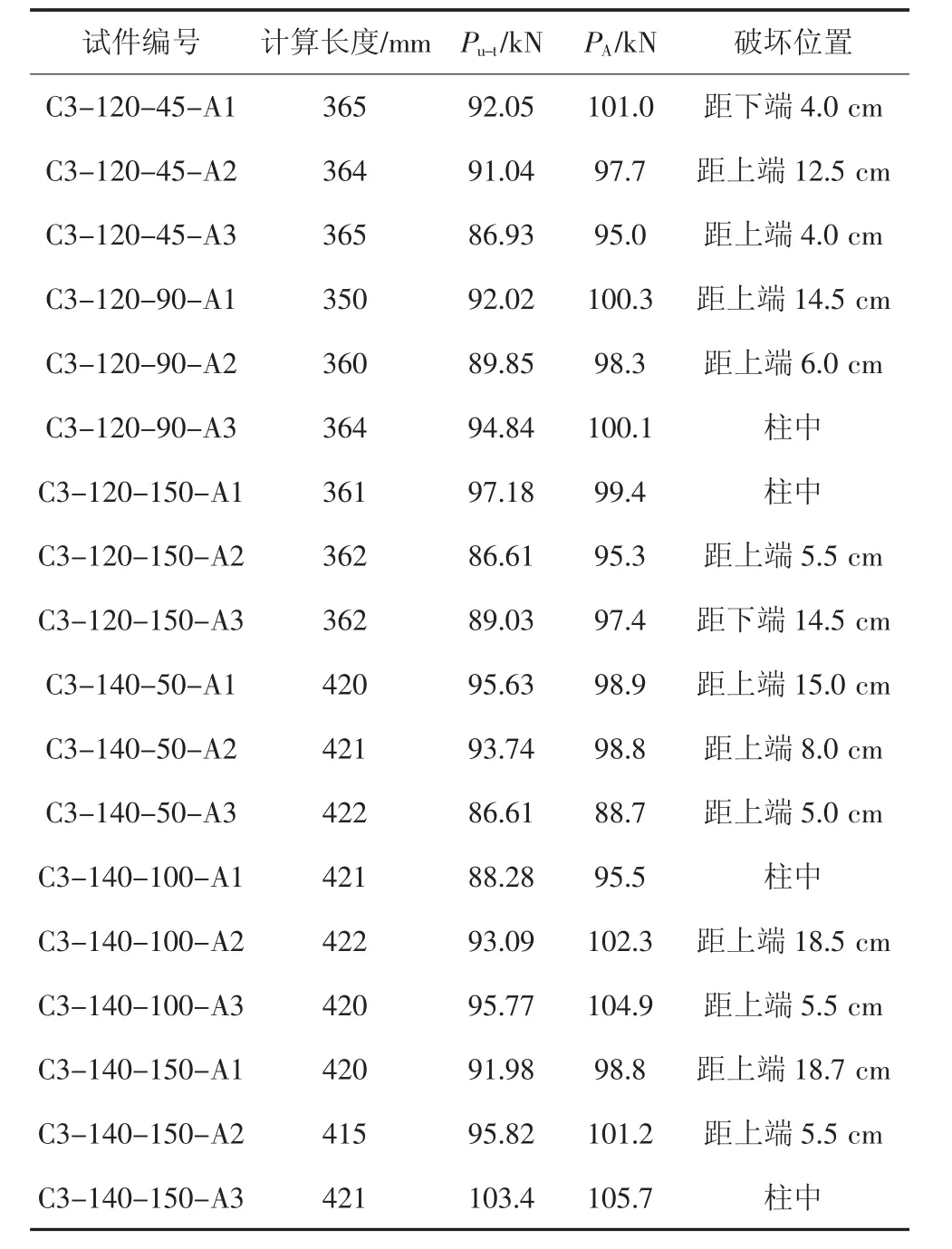
表2 试验试件的承载力Tab.2 Bearing capacity of the test specimens

2.2 荷载-轴向位移曲线

试件的轴向位移是通过布置在上端板的位移计测量的，具体如图12 所示.由图12 可得出，各组试件在加载初期，荷载-轴向位移曲线保持线性增长，说明各试件刚度基本不变；接近极限荷载时，试件的曲线不再呈线性增长，刚度略下降；但达到极限荷载以后，曲线呈非线性下降，且荷载快速降低，位移快速增大，直至试件发生塑性破坏.除个别试件外，同组各个试件的刚度几乎一致.

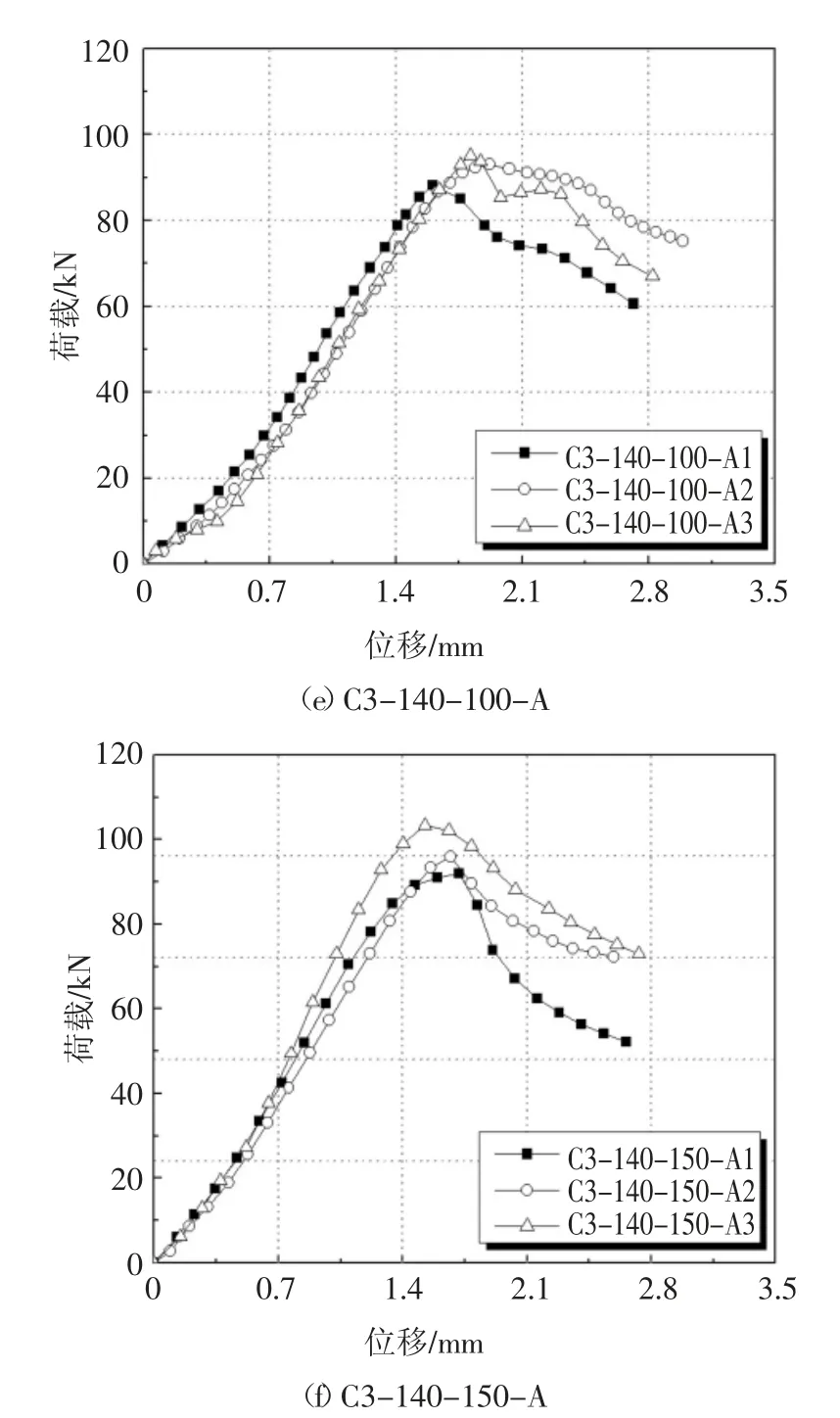
图12 荷载-轴向位移曲线Fig.12 Load-axial displacement curve

3 有限元分析

3.1 有限元模型的建立

采用ABAQUS[15]软件建立有限元模型，试件的上下端板均采用解析刚体单元，柱子采用S4R 壳体单元，螺钉采用C3D8R 实体单元.柱网格划分尺寸为5 mm×5 mm，螺钉为1 mm×1 mm，有限元模型如图13 所示.有限元模型采用理想弹塑性模型，屈服强度fy为289.24MPa，泊松比ν 为0.3，弹性模量为1.899×105MPa.

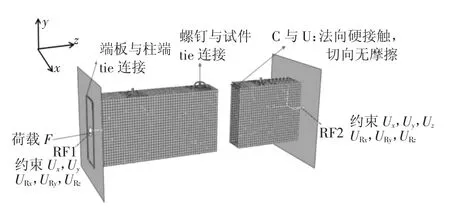
图13 有限元模型Fig.13 Finite element model

柱端与端板直接tie 在一起以模拟现实焊接情况.另外，选择螺栓为主面，两个基本构件与螺栓接触部分为从面将其tie 在一起.边界条件保持与试验一致，均为两端固结，通过约束上端板中心参考点RF1 的Ux、Uy方向的2 个平动自由度与3 个转动自由度（URx、URy、UR）z以及下端板中心参考点RF2 的6个自由度（Ux、Uy、Uz、URx、URy、UR）z以实现固结，在参考点RF1 上施加轴向位移载荷，如图13 所示.

3.2 有限元模型正确性验证

为验证有限元模型的正确性，本文采用试验试件的实际测量尺寸建立模型，通过有限元分析结果与试验结果对比，验证有限元模型的正确性和合理性.建立模型时，本文充分考虑了试件的加工及焊接误差，通过特征值分析在屈曲变形较大的模态下引入初始缺陷.以下以C3-120-90-A 试件为例，将其有限元模型与试验比较，如图14 所示.

由图14 可知：C3-120-90-A1 和C3-120-90-A3 破坏位置均在腹板和翼缘中间，而C3-120-90-A2 的破坏位置靠近试件上端，分析其主要原因是试件加工及焊接误差导致.但综合考虑，各个试件有限元分析的破坏位置和试验吻合较好，符合要求.分析表2 可得：试件有限元极限承载力普遍比试验值高出2%～10%，且在允许误差范围内，结果表明本文建立的有限元模型是准确可靠的.

3.3 有限元变参数分析

图14 C3-120-90-A 系列试件有限元和试验对比Fig.14 Comparison of the finite element and test of the C3-120-90-A series specimens

腹板高厚比不仅对局部屈曲轴压拼合柱临界荷载有很大的影响，也是影响其极限承载力的重要因素.为研究其影响规律，本文设计4 种长度的试件：270 mm、360 mm、450 mm 和600 mm.每种长度的试件有3 种翼缘宽度尺寸.另外，在此基础上本文设计4 种截面厚度：0.8 mm、1.0 mm、1.2 mm 和1.5 mm，腹板高厚比变化范围为60～250，共48 个试件.有限元结果见表3，且由表3 可得以下结论：

1）腹板高度为90 mm 的系列柱，当腹板高厚比从60 增至112.5 时，3 种翼缘宽度拼合柱的极限承载力降低63.1%～65.6%；对于腹板高度为120 mm 的系列柱，当腹板高厚比从80 增至150 时，3 种翼缘宽度拼合柱的极限承载力约降低64.1%～66.2%；对于腹板高度为150 mm 的系列柱，当腹板高厚比由100 增至187.5 时，3 种翼缘宽度拼合柱的极限承载力约降低63%～65.4%；对于腹板高度为200 mm 的系列柱，当腹板高厚比由133.3 增至250 时，3 种翼缘宽度拼合柱的极限承载力约降低63.4%～66.4%.

2）4 个系列12 个试件，每组试件的极限承载力随着腹板高厚比增加显著降低.除个别试件外，腹板高厚比每增大25%，极限承载力降低幅度均为30%.因此腹板高厚比是影响拼合柱极限承载力的重要因素.

4 承载力叠加法的提出

为研究CFS 局部屈曲拼合箱形截面短柱的承载力计算方法，本文提出一种不同于中国规范GB 50018—2002[12]、美国规范AISI[13]有效宽度法（EWM）和直接强度法（DSM）的计算方法——承载力叠加法.具体计算方法：以DSM 中的局部屈曲承载力计算公式计算出拼合箱形截面短柱基本组成构件单肢C 形构件的极限承载力Pu1，再以文献[16]修正后的局部屈曲承载力公式计算单肢U 形构件的极限承载力Pu2，然后将Pu1和Pu2进行叠加再乘以组合系数α 得到以直接强度法计算的拼合箱形截面柱的叠加承载力.而组合系数α 是通过有限元参数分析结果PA和Pu1与Pu2之和Pua回归分析得到的，通过线性回归最后提出拼合箱形截面柱极限承载力的计算公式模型为：Pu=α（Pu1+Pu2）+a，如图15 所示.

4.1 单肢构件承载力计算

1）单肢C 形截面计算公式：

表3 不同高厚比的极限承载力结果Tab.3 Ultimate bearing capacity results of different ratios of height-to-thickness

图15 理论值与有限元值回归曲线Fig.15 The regression curve between theoretical value and finite element value

式中：λ1=指C 形构件的局部屈曲临界荷载，fcr1为C 形构件的局部屈曲临界应力，fcr1借助有线条软件CUFSM[17]计算获得.

2）单肢U 形截面计算公式：

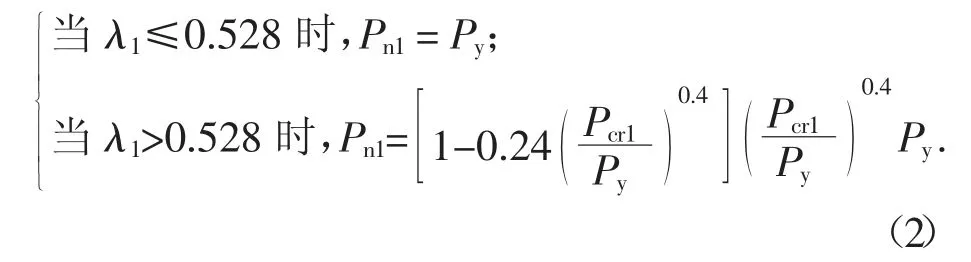
式中：Pcr1=Agfcr1，Pcr是U 形构件的局部屈曲临界荷载，fcr1是U 形构件的局部屈曲临界应力，Pcr借助广义梁GBTUL[18]软件获得.

4.2 CFS 拼合箱形截面短柱承载力叠加法

将本文有限元分析设计的48 根试件综合分析，其横截面的h/t、b/t、h/b、b/d 等参数变化范围均较广.具体的回归方法是：在基本组成构件承载力计算公式（1）和（2）计算出单肢C 形和单肢U 形构件承载力Pu1和Pu2的基础上，通过将变参数试件的基本组成构件Pu1与Pu2之和Pua与有限元分析得出的拼合柱极限承载力进行对比回归，以Pua为横坐标，以有限元分析结果PA为纵坐标，回归得到CFS 拼合箱形截面短柱承载力的公式，如图15 所示，具体数据见表4.由图15 知，皮尔逊相关系数为0.995，Adj.RSquare 相关系数为0.990，说明CFS 拼合箱形截面柱基本组成构件理论计算叠加值与拼合箱形构件有限元分析值呈线性相关，回归直线与纵轴的截距为2.94，斜率为1.09，即组合系数α 为1.09.因此，由以上分析得出CFS 局部屈曲拼合箱形截面短柱承载力叠加法公式如式（3）所示.

表4 有限元值与理论计算值对比Tab.4 Comparison of finite element value and theoretical value kN

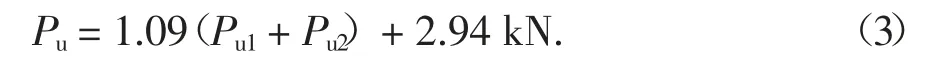
4.3 本文叠加法的验证

将试验数据代入公式（3）进行验证，见表5.观察表5可知，Pt/Nu，Pt/NUSA-e均值和标准差分别为1.33，1.28 和0.055，0.054，并且试验值比GB 50018—2002、EWM 计算结果均高25%以上；Pt/NUSA-d，Pt/Pu均值和标准差分别为0.96、1.04 和0.053、0.035，由此可知DSM 和本文方法与试验结果接近（见图16），但美国规范的DSM 计算结果离散性大且总体偏于不安全.因此，分析结果表明本文计算方法理论值与试验值吻合较好，计算结果精确度较高，规律性较强，且离散性较小，说明本文提出的计算方法是精确且可靠的.

表5 中美规范及提出方法的计算结果与试验结果对比Tab.5 Comparisons of calculation results and test results between Chinese and American codes and the proposed method kN

图16 不同计算方法对比Fig.16 Comparison of different calculation methods

5 结论与讨论

1）通过分析试验现象和试验数据，发现改变螺钉间距对拼合箱形截面短柱的极限承载力影响很小，在考虑初始缺陷的情况下，螺钉间距对拼合箱形截面短柱的极限承载力的影响在12%以内.

2）变腹板高厚比的试件均发生局部屈曲破坏，且其极限承载力随着截面腹板高厚比的增加显著降低.结果表明腹板高厚比是影响CFS 拼合箱形截面短柱极限承载力的重要因素.

3）中国规范GB 50018—2002 和美国规范EWM对于冷弯薄壁型钢拼合箱形截面柱的局部屈曲承载力计算理论偏保守，且随着高厚比的增大，计算结果变得越来越偏于保守.美国规范DSM 计算值普遍高于试验值，相差在10%以内，说明用美国规范直接强度法计算局部屈曲拼合箱形截面轴压柱试件的极限承载力是偏不安全的.而本文提出的叠加法计算值比美国规范DSM 更加精确合理.

4）本文基于直接强度法提出的承载力叠加法，解决了计算CFS 拼合箱形截面短柱的极限承载力的问题，可为该类截面的实际工程设计提供参考.

5）本文只研究了螺钉间距对CFS 拼合箱形截面短柱承载力及屈曲半波长的影响，且螺钉间距变化对该类局部屈曲试件的极限承载力影响很小.此外，针对发生畸变屈曲和整体失稳的试件，螺钉间距对CFS 拼合箱形截面柱的承载力及屈曲半波长的影响规律有待进一步研究.