古建筑彩绘梁整像素位移自适应搜索解算方法

2020-11-21刘纲李孟珠蒋伟张维庆

湖南大学学报（自然科学版） 2020年11期

刘纲，李孟珠，蒋伟，张维庆

（1.山地城镇建设与新技术教育部重点实验室（重庆大学），重庆 400045；2.重庆大学土木工程学院，重庆 400045）

中国古建筑具有悠久的历史传统，是当时科学技术水平和人民社会生活状况的真实见证，具有重要的历史、艺术和科学价值[1].在以木结构为主的古建筑中，受木材蠕变、腐蚀、虫蛀和长期荷载作用[2-3]，木质构件变形过大问题较为普遍[4]，木结构变形监测可用于判断变形发展趋势、提供结构受力计算所需变形数据，是古建筑木结构预防性保护的重要手段.

传统上古建筑变形测量以接触式方法为主，例如在结构构件上布置观测点或粘贴光纤传感器[4-5]，这些方法对古建筑构件有一定程度的破坏，不利于古建筑保护.虽然近年来无需在古建筑上布设测试点的免棱镜技术得到快速发展，但是其测试精度受较多因素限制，在部分条件下较难满足工程测试要求.近年来，非接触式变形测量方法得到快速发展，其中，基于数字图像相关（Digital image correlation，DIC）原理[6]的测试方法随着摄像技术、计算能力的提升得到了大力发展，已在航天、机械和土木工程领域得到实际应用.DIC 法最早可追溯到20 世纪80 年代，美国南卡罗莱纳大学Peters 等[7]针对材料表面均匀拉伸应变测量提出基于DIC 进行位移测量的思路；Sutton 等[8]针对全场平面内变形的整像素位移搜索，提出粗-细搜索法，从而提高整像素级图像匹配的计算速度.Gencturk 等[9]将DIC 法应用于预应力混凝土位移测量，结果表明该方法可准确测量预应力混凝土变形信息.奥村运明等[10]应用DIC 法进行古建筑墙体裂缝观测，结果显示该方法能满足工程上裂缝测量的要求.

DIC 法通过在被测结构表面喷涂具有一定特征的散斑图，然后利用结构位移前后散斑图的变化来识别结构变形[11]，而中国古建筑木结构的表面往往装饰有彩绘图案[12]，故利用彩绘图也可实现位移测量.但应指出的是，与特制散斑图相比，彩绘图灰度梯度分布不均且存在大块灰度近似区，故直接采用现有DIC 位移解算方法将无法保证位移测试精度.针对这一问题，在现有自适应十字模式搜索方法（Adaptive Rood Pattern Search，ARPS）的基础上，提出局部穷举-自适应十字模式搜索方法（Improve-APRS，IARPS），提高整像素位移搜索精度，从而增强古建筑彩绘图位移辨识精度，并提升位移辨识计算的稳定性和效率.通过实验验证所提方法的适用性，并与常用整像素位移解算方法进行对比，为古建筑木结构非接触式位移测量提供新的解算方法.

1 基于DIC 原理的位移测试

1.1 位移测试原理

基于DIC 原理的位移测试技术在被测构件上喷涂特制散斑图，借用数字摄影技术将散斑图在相机感光组件上成像，然后通过匹配变形前后数字图像像素的变化，从而获得被测物体表面各点的位移信息，该方法的位移辨识原理如图1 所示.

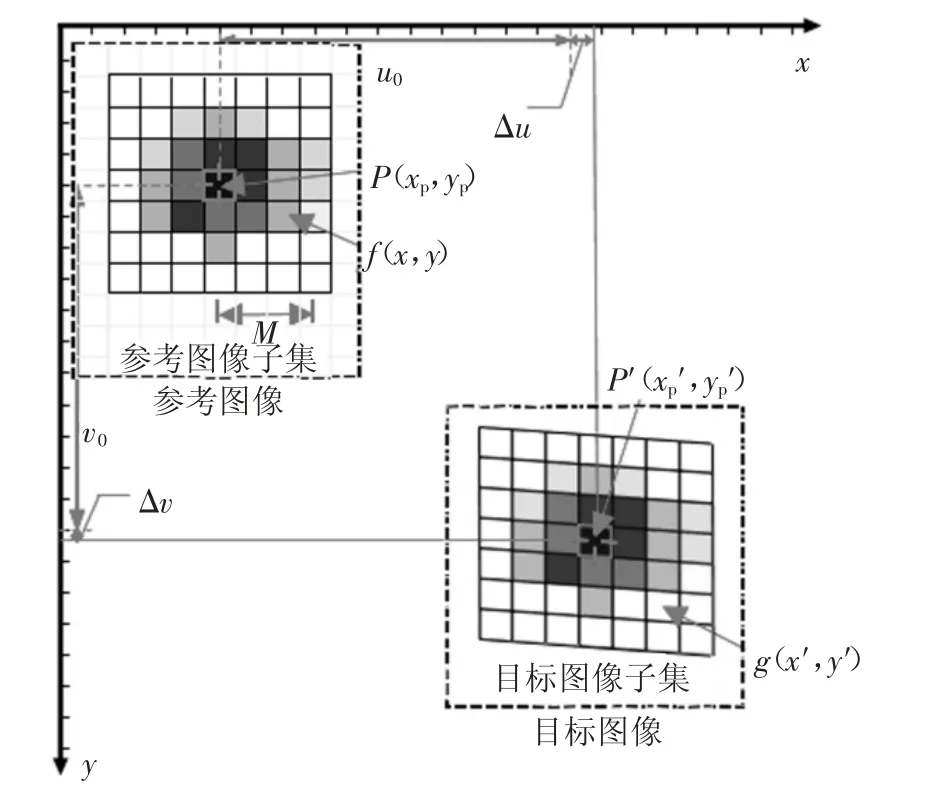
图1 二维DIC 位移辨识原理Fig.1 Displacement identification principle of two-dimensional DIC

在图1 中，一个小方格代表数字图像上的一个像素，变形前的图像称为参考图像，变形后的图像称为目标图像.针对参考图像、目标图像建立统一的坐标系x-y，参考图像中（x，y）处像素点的灰度值为（fx，y）；目标图像中（x′，y′）处的像素点灰度值为g（x′，y′）.设参考图像中P 点坐标为（xp，yp），目标图像中与P 点对应的P′点坐标为（x′p，y′p），DIC 方法计算P′点到P 的距离可分为以下几个步骤：

1）在参考图像中，选取整数M，然后选择一个计算点P（xp，yp），以该点为中心选取（2M+1）×（2M+1）像素大小的区域为计算子集，其中2M+1 称为子集半径.

2）在目标图像中，任选一点并作为搜索点，以该点为中心，框选（2M+1）×（2M+1）的计算子集，再计算相关系数CZNSSD：

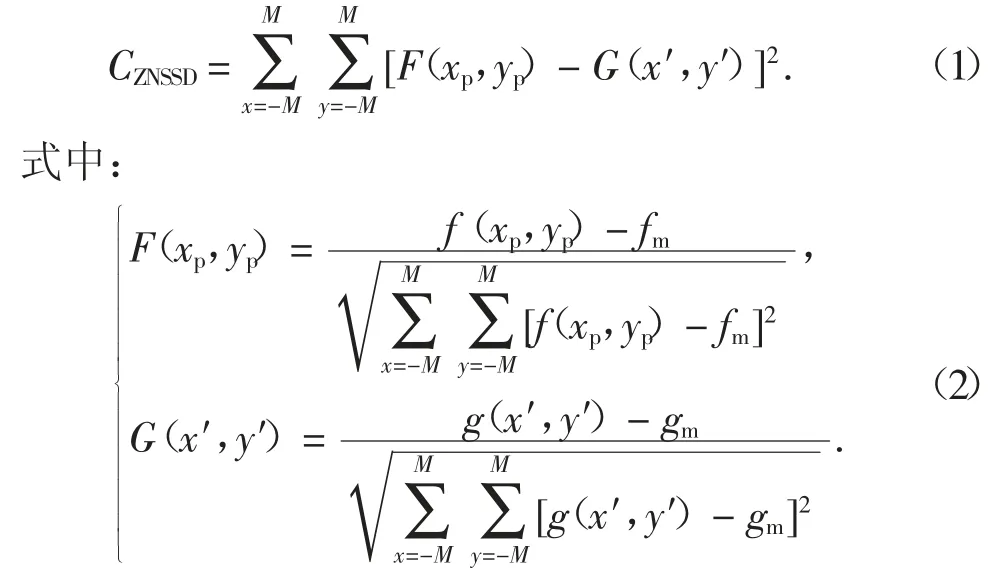
式中：fm表示参考图像子集的灰度平均值；gm表示目标图像子集的灰度平均值.然后，通过一定的搜索方法计算多个点的相关系数，并将相关系数最值点对应的搜索点作为P′点的匹配点.此时，可确定P 点整像素x 向位移up、y 向位移vp.

3）根据求得的匹配点的坐标，在（xp+up，yp+vp）像素点相邻1 个像素范围内通过一定方法进行亚像素位移搜索，得到P 点分别在x、y 向亚像素位移Δup、Δvp.

4）根据求得的整、亚像素位移，最终解算得到P点x 向位移u、y 向位移v 分别为：

从以上步骤可知，DIC 法先执行整像素位移搜索，并将搜索结果作为亚像素搜索的初始值，故整像素搜索算法不但决定整像素搜索精度，也将影响亚像素搜索精度.因此，整像素搜索算法对位移辨识精度的影响较大.

需指出的是，第一次在目标图像中任选一点时，若该点距图像边缘的距离小于2M+1，则无法以该点为中心组成计算子集，称为边缘问题.为避免这一问题，可在初次选择计算点时进行预判：若计算点不存在边缘问题，则进行以上步骤的搜索；若不满足，则重新选取计算点，直至找到不存在边缘问题的计算点.

1.2 整像素粗-细搜索算法

目前，DIC 中最常用的整像素位移搜索算法有粗-细搜索法（Coarse-Fine Search，CFS）[13]、三步搜索法[14]及菱形搜索法[15]等，其中CFS 算法的精度和计算效率相对较高，其位移搜索的基本思路为：将整个目标图像视为搜索区域，首先采用较大的计算步长计算相关系数，以相关系数极小值对应的搜索点为本轮搜索的匹配点；然后以此匹配点为中心，缩小搜索区域及计算步长选取搜索点进行下一轮搜索；最后，当计算步长缩小为1 像素时，可得P′点的匹配点，进而计算得到该点的整像素位移.

1.3 搜索算法精度评价指标

设参考图像和目标图像的像素均为I×K，则两幅图像的均方误差MES 定义为：

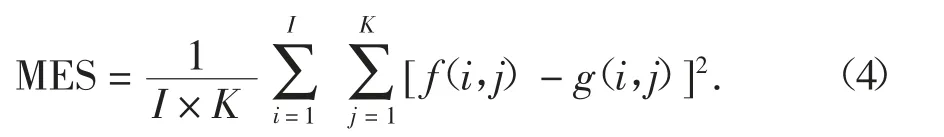
两幅图像的峰值信噪比（Peak-Signal-to-Noise-Ratio，PSNR）定义为：

式中：MAXI表示图像灰度的最大值，对于采样点用8 进制表示的灰度图像取255.峰值信噪比可评价两幅图像子集的近似性，近似程度越高，PSNR 系数越高，即搜索算法的精度越高.

2 修正的自适应十字模式整像素搜索法

2.1 自适应十字模式整像素搜索法

CFS 算法假定每一轮最佳匹配点处的相关函数值CZNSSD单调减小，即由相关系数组成的二维曲面是单峰的.通常情况下，由散斑图得到的二维曲面可能存在几个局部极值现象，如图2（a）所示.此时，只要计算步长选择合适，CFS 仍可搜索到正确结果.但对于彩绘图像，由于其灰度分布不均，所得相关函数曲面往往存在多峰现象，在CFS 搜索过程中的单调性不复存在，如图2（b）所示.此时，初始计算步长对CFS 算法精度甚至正误影响很大，而初始计算步长通常由人工主观选取，具有很大的随机性.

为克服计算步长选取的随机性，Nie 等[16]提出了自适应十字模式搜索法（Adaptive Rood Pattern Search，ARPS）.其基本思路是，假设物体的变形是连续的，在进行整像素位移搜索时，采用相邻已知位移像素点的位移作为搜索初值，其具体搜索步骤为：

图2 单峰与多峰曲面示意图Fig.2 Schematic figure of unimodal and multimodal surfaces

1）对参考图像中的某计算点P，设其在x-y 坐标系中的坐标为（u1，v1）；记P 相邻像素点已知整像素位移为（u，v），记R=max（|u|，|v|），R=（u，v）.在目标图像中，以坐标（u1，v1）所在的像素点为中心点O，若是第一个计算点，则在该点沿x-y 轴向相距2 像素的上下左右各选1 个点，形成十字形搜索模式；若不是第一个计算点，则在该点沿x-y 轴向相距R 像素的上下左右各选1 个点，形成十字形搜索模式，同时选取R 为一个搜索点，共计5 个搜索点，如图3（a）中黑色小圆点所示.

2）按式（1）计算图3（a）中5 个搜索点的相关系数，选取相关系数最小值所在点为初始匹配点.以初始匹配点为中心，选取该点及上下左右4 个相邻像素点形成单位十字搜索模式，并将这5 个点作为新的搜索点，如图3（b）所示.

3）按式（1）计算单位十字搜索模式中5 个搜索点的相关系数，若最佳匹配位置为单位十字搜索模式的中心点，则结束搜索，该点即为计算点P 的最佳匹配点P′（u2，v2）；否则，将单位十字中心移至新的相关系数最小点，重复进行单位十字模式搜索，直至相关系数最小点为十字搜索模式的中心为止，此时十字模式的中心点即为计算点的最佳匹配点P′.

4）根据求得的最佳匹配点P′的坐标（u2，v2），可解算P 点的整像素位移（u2-u1，v2-v1）.

当计算参考图像中的第一点时，其相邻点位移为未知，故在第1）步中仅采用十字形搜索模式的4个点进行搜索，其余步骤与以后各计算点的步骤相同.

2.2 基于局部穷举的自适应十字模式搜索法

ARPS 法根据相邻像素已知位移自适应调整步长，有利于解决相关系数曲面存在多个极值的问题，但对第一个位移搜索点的位移初值采取零位移假设（仅采用4 个搜索点进行计算），可能带来一定的误差.为解决该问题，可先预估第一个位移搜索点的位移最大值，并将其作为初始搜索半径，进行局部穷举搜索，从而为后续各搜索点的位移计算提供准确的初值.局部穷举搜索具体步骤为：

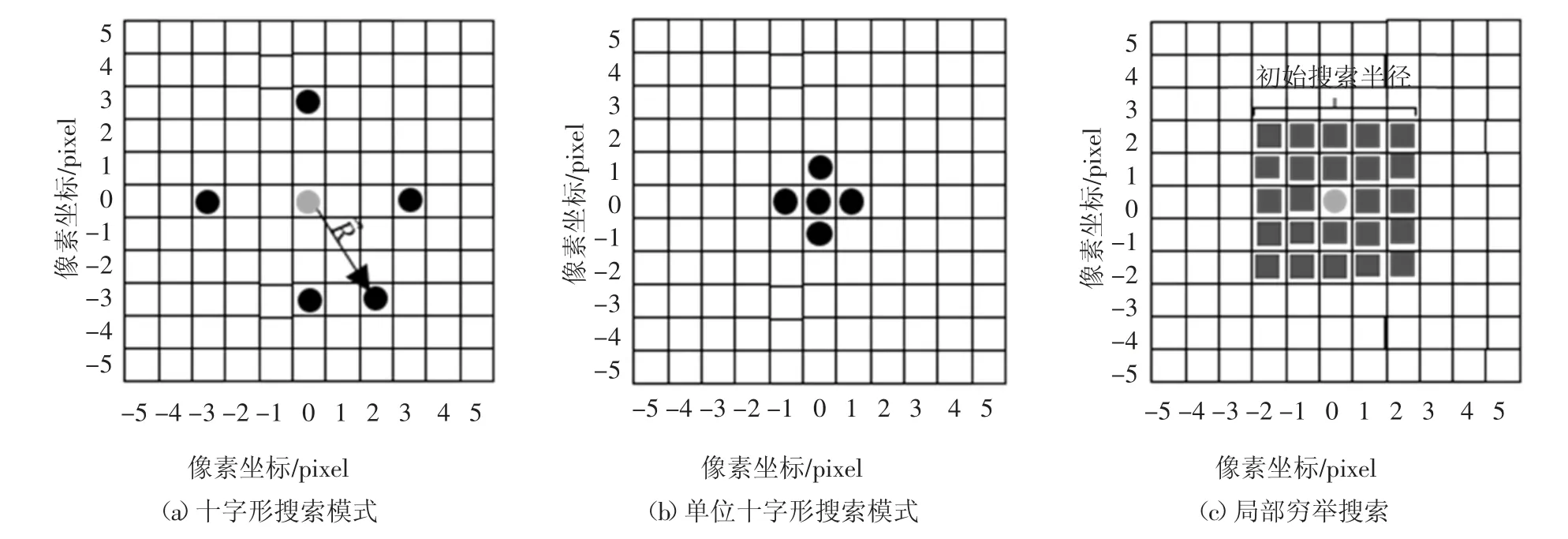
图3 整像素搜索法示意图Fig.3 Schematic figure of integer pixel search

1）对于参考图形中的某搜索点P，已知其在x-y坐标系中的坐标为（u1，v1）；在目标图像中，以坐标（u1，v1）所在的点为中心点，选择一个初始搜索半径，如图3（c）所示，在该方形区域内对每个点进行局部穷举搜索.

2）针对方形区域内的每一个点，计算所有点的相关系数.

3）选取所有搜索点中相关系数最小点为第一个初始计算点的最佳匹配点，然后按照ARPS 法的第2）～4）步计算该点位移.

4）按照ARPS 方法的第1）～4）步计算剩余各计算点的位移.

采用穷举搜索可确保搜索到精确的位移初始向量，避免陷入图2（b）所示的错误局部最优解，将增加局部穷举搜索后的ARPS 法称为修正的自适应十字模式搜索法（Improved-ARPS，IARPS）.

3 实验验证

3.1 实验设置

分别通过模拟散斑图发生刚体位移、实验室木梁彩绘图变形实验对比IARPS 算法与CFS、ARPS 算法的区别.

3.1.1 散斑图位移模拟

采用Zhou 等[17]提出的散斑图生成算法得到256×256 像素的散斑图作为参考图像，其中高斯光斑数目为1 000 个，高斯光斑大小为4 像素，高斯光斑的中心光强为0.7.将参考图像在y 向移动6 个像素作为目标图像，即目标图像各整像素点的位移向量均为（0，6）.为模拟测试噪声，在目标图像中加入均值为0，标准差为2 的高斯白噪声.为节约篇幅，将参考图像、目标图像分左右两幅给出，如图4 所示.

图4 模拟散斑图像Fig.4 Simulated speckle image

在散斑图中，仅计算图4 中虚线所在像素点发生的位移，该虚线由90 个像素点组成，其像素坐标自上而下定义为1～90 pixel.

3.1.2 彩绘图实验

在实验室中采用长宽高分别为2 000 mm×40 mm×25 mm 的木梁进行实验，将规则花纹粘贴于梁中部侧面.采用重物分两次在跨中加载，使梁产生挠度，分别记为工况1 和工况2，并在跨中安装千分表对辨识位移的精度进行验证，具体的加载装置如图5所示.实验中采用的图像采集系统为VIC-2D，相机型号为GZL-CL-41C6M-C，其分辨率为2 048×2 048像素.将相机放置在彩绘梁正前方约2 m 处，并使其光轴对准梁的形心且与彩绘图案面垂直，将相机与计算机相连并用测试系统的软件进行图像采集.

3.2 实验结果分析

考虑到穷举搜索法（Exhaustive Search，ES）将计算搜索指定范围内所有可能的像素点，其计算精度在所有的搜索算法中最好，故采用该算法作为基准验证其他整像素解算方法的精度.

图5 实验加载装置Fig.5 Experimental loading device

为方便与千分表测试结果对比，取千分表正上方虚线所对应像素进行位移辨识，共包括90 个像素点，从上向下依次定义为1～90 pixel.一个像素对应的实际长度为25 mm/90=0.278 mm.计算子集中M取为15，则一个子集包含31×31 像素.

CFS 及IARPS 法计算的PSNR 结果如图6 所示.由图6（a）可知，对于散斑图的整像素位移解算，CFS、IARPS 法均可达到与ES 法相同的精度，这主要是因为散斑图的灰度分布较均匀，其相关函数组成的二维曲面是单峰的，相关系数往往单调减小，故所有方法均可达到一样的精度；但对于ARPS 算法而言，在像素坐标1 处的精度较低，这是由于假定的初始假设位移为（0，0），不能精确解算第一个搜素点的位移.从图6（b）可看出，在不同像素坐标处，CFS 法对彩绘图位移的解算精度会出现降低现象，例如从像素坐标13 到20；APRS 法在像素坐标1 处的精度也较低，而IARPS 法对所有像素坐标的解算精度均与ES 法相同，这主要是因为IARPS 法可精确计算第一个搜索点的整像素位移，且继承了ARPS 高效的自适应性，因此，可有效克服传统算法局部计算不精确的缺陷，比APRS、CFS 更适合灰度不均匀彩绘梁位移测量.

图6 不同整像素识别算法的PSNRFig.6 PSNR of different integer pixel recognition algorithms

采用算法对相关函数的调用次数作为计算效率的评价指标，调用次数越多，计算效率越低.4 种方法的计算效率比较如图7 所示，由于ES 方法是对于全局搜索的，而且ES 方法只起对比作用，因此为使图像美观，ES 方法也选择跟其他算法一样的8 像素的搜索半径.

从图7 可知，穷举法在每个像素点处均需289次相关函数运算；CFS 法在不同的搜索点处大约需43 次相关函数运算；而IARPS 法除在第一个像素点处需局部穷举计算，需298 次相关函数运算之外（除局部的穷举搜索外还进行了自适应的搜索，因此搜索次数大于ES 法搜索次数），其余各像素点则需9次相关函数运算.针对90 个整像素点的位移解算，IARPS 法较CFS 法的计算效率提高71.6%，因此IARPS 法总体上具有较高的计算效率.

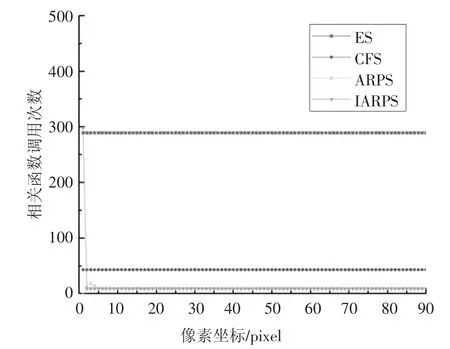
图7 计算效率对比Fig.7 Comparison about calculation efficiency

在整像素搜索的基础上，采用常用梯度亚像素搜索法进行亚像素位移辨识，得到的位移识别结果与千分表的测试结果见表1.当仅采用整像素的识别结果时，相对误差高达6.05%，这主要是由于1 个像素对应的位移精度仅为0.278 mm，而整像素搜索结果误差必然大于该精度，故误差较大.采用亚像素搜索后，相对误差可降低到0.064%，小于千分之一.因此，所提IARPS 算法与常规的亚像素识别算法结合后可用于古建筑构件的非接触式位移测试.

表1 位移识别结果对比Tab.1 Comparison of displacement recognition results mm

3.3 参数分析

3.3.1 初始搜索半径大小

对于彩绘图实验，采用90 个像素点PSNR 系数之和——SUM-PSNR 来衡量不同初始搜索半径下不同算法的解算精度，结果如图8 所示.

由图8 可知，CFS 法的初始搜索半径要达到6像素以上才能有较高的SUM-PSNR 系数，即初始搜索半径大于像素点实际位移时才能较精确地识别整像素位移.取不同搜索半径时，ARPS 法的识别精度较IARPS 低，这主要是因为初始计算点假设选取的缘故，IARPS 法的搜索半径仅为4 像素时就能达到与ES 相同的精度，这是由于IARPS 法中尽管第一步局部穷举方法识别结果存在少许误差，但是之后的自适应搜索部分依然可以进行快速纠正，并保证计算结果的精确性.

图8 初始搜索半径对识别结果的影响Fig.8 Effect of initial search radius on the recognition results

3.3.2 图像噪声分析

采用初始搜索半径为8 像素，给模拟散斑图、彩绘图分别添加均值为0，标准差为1～10 的高斯白噪声，以测试图像噪声对整像素位移识别的影响，结果如图9 所示.

由图9 可看出，不管是散斑图还是彩绘图，随着噪声标准差的逐渐增大，SUM-PSNR 系数逐渐降低，表明噪声将降低目标图像与参考图像之间的相关性.对散斑图而言，在噪声影响下，CFS、IARPS 法的识别精度与ES 法相当，这主要是因为散斑图灰度分布较均匀，CFS 法可获得较好的解算精度，但ARPS的精度略低，这是由于该方法在计算第一个搜索点位移时有较大误差所致；对彩绘图而言，仅IARPS 法与ES 法的识别精度相当，且CFS 法的精度比ARPS法更差，这主要是因为相同噪声水平下，灰度分布不均匀导致相关系数曲面出现多峰情况，导致CFS 精度大幅下降所致.