固体折射率的激光散斑测量实验

许惠敏，黄若楠，雷豪洁，丁焕林，何俊达，罗劲明

(嘉应学院 物理与电子工程学院，广东 梅州 514015)

物质的折射率是表征物质光学性质的重要物理参数，广泛应用于光学、材料、化工、食品、医疗等各种领域，因此物质折射率的测量与高校科研、工业生产和生活等息息相关，是现代科学领域的一个热门研究话题。

激光散斑，是激光自散射体的表面反射或通过一个透明散射体时，在散射表面或附近经散射光干涉形成的一种无规则分布的亮暗斑纹，简称散斑。散斑按照光场的传播方式，可以把散斑分成远场散斑(与夫琅和费衍射对应)、近场散斑(与菲涅耳衍射对应)和像面散斑三种类型。目前，散斑已经广泛地应用在表面粗糙度研究、光学图像处理和成像质量评价等方面，其中最有应用前景的就是散斑计量，如散斑照相、散斑光弹、散斑干涉、散斑数字滤波和散斑图像处理等技术[1-5]，而透明固体折射率的测量则是其应用之一[6-8]。本文分别采用现有方法和改进方法测量了固体玻璃的折射率，并进行了实验对比研究。

1 基本原理与方法

1.1 基本原理

利用激光散斑法测量透明固体介质的折射率[9]，主要是通过测量散斑在放入具有一定倾斜角的透明固体(平行平板)前后，因折射效应而产生的微小面内偏移量，进而通过理论公式计算出透明固体折射率。

如图1所示，当一束光照射到一倾斜的透明固体时，将产生折射。其中

(1)

以及

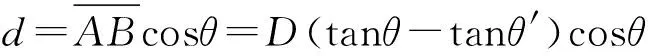
(2)

式中，θ为入射角(等于透明固体的倾斜角)，θ′为折射角，D为透明固体的厚度，d为散斑面内偏移量。

图1 透明固体的光学折射特性

由折射定律

n0sinθ=nsinθ′

(3)

其中，空气的折射率n0=1，n为透明固体的折射率。

联合(1)(2)(3)式，可得

(4)

公式(4)表明，如果已知透明固体的厚度D、倾斜角度θ,只有测量出面内偏移量d，即可获得固体的折射率n。

散斑面内偏移量的测量d，一般是通过在同一个记录平面采集变化前后的两幅散斑图，然后寻找在这两个相同但位置稍微错开的散斑图中的“散斑对”，即在绝大多数变化前散斑图上的散斑点都能在变化后散斑图上找到对应的散斑点，使得散斑点成对存在，而散斑对的距离和方向反映了物体变化前后的偏移大小以及方向。传统全息通常利用逐点分析法[9]测量散斑面内偏移量，即利用细激光束照明散斑图，使照明区域中的“散斑对”发生杨氏双孔干涉，通过对观察距离和干涉条纹间距的测量，可计算出“散斑对”的距离(面内偏移量)；而数字全息通常利用数字图像相关法[10]测量散斑面内偏移量，即对位移前的散斑图像选取一定大小的基元散斑图，与位移后的散斑图像进行相关计算(寻找相应的“散斑对”)，则在相关系数最大的位置将会输出一个相关亮点，对这个相关亮点的位置坐标进行识别，即可测量出散斑面内偏移量。

然而，需要解决的关键问题是，散斑在放入透明固体前后产生的轴向偏移量对“散斑对”的影响。如图1所示，考虑未放固体前在空气中传播会聚的某一散斑点S，在放入待测透明固体后，由几何光学可知与之对应的散斑点S1不仅在记录平面有面内偏移，而且在光轴方向也产生轴向偏移，这一轴向偏移使“散斑对”不在一个平面上，导致记录平面采集到的两幅散斑图并不完全相同，从中难以找到相应的“散斑对”，因而产生测量误差。

1.2 基本方法

1.2.1 方法一(现有方法)

先采集一幅未放待测透明固体时激光通过空气的散斑图，再将待测透明固体放入光路系统中，并偏转一定的角度，在同一记录平面上再采集一幅激光通过固体的散斑图，通过这两幅散斑图获得散斑面内偏移量，进而理论计算出其折射率。

1.2.2 方法二(改进方法)

先采集一幅待测透明固体垂直光轴放置时激光通过固体的散斑图，然后将固体偏转一定的角度，在同一记录平面上再采集一幅倾斜放置后激光通过固体的散斑图，然后获得激光通过透明固体前后的散斑面内偏移量，并根据公式计算出其折射率。

2 结果与分析

本文搭建了近场散斑法、远场散斑法和像面散斑法三种测量光路，分别采用了方法一和方法二，利用氦氖激光器(λ为632.8 nm)测量了厚度为3 mm的透明固体(玻璃)折射率(折射率约为1.5)。

2.1 近场散斑法测量固体折射率

近场散斑法测量光路如图2所示，氦氖激光器发出的激光经扩束准直后，获得的平行光照射到毛玻璃形成散斑，散斑图像通过透明固体玻璃后被记录平面接收。

图2 近场散斑法的测量光路示意图

首先采用传统全息进行实验，实验设定随机倾角θ为0.083 rad，通过天津I型全息干板记录两张散斑图，经显影、定影和漂白后，采用逐点分析法观察到的干涉条纹如图3(a)所示。结果表明，利用方法一无法观察到任何干涉条纹，而方法二则可以观察到清晰的干涉条纹。通过对方法二的干涉条纹进行测量分析，得到的微小偏移量d为0.08 mm，将相关参数值代入公式(4)进行计算可以获得玻璃折射率n为1.48。

为了进行对比，同样利用这一近场散斑测量光路，采用数字全息进行实验，其数字图像相关结果如图3(b)所示。其中，方法一的散斑相关图有一个较亮的斑点，但出现明显的弥散点分布，这些弥散点对散斑面内偏移量的测量形成干扰，使其玻璃折射率n的测量值为1.58；而方法二则是一个明显的相关亮点，没有任何弥散点的干扰，因而其测量精度较高，其玻璃折射率n的测量值为1.50，与参考值非常接近。

(a)传统全息

2.2 远场散斑法测量固体折射率

远场散斑法测量光路如图4所示，毛玻璃放在变换透镜的前焦平面，而记录平面则放在透镜的后焦平面，氦氖激光器发出的激光经扩束准直后，获得的平行光照射到毛玻璃形成散斑，散斑图像通过透镜和透明玻璃后被记录平面接收。

图4 远场散斑法的测量光路示意图

传统全息实验设定随机倾角θ为0.1 rad，根据以上流程，首先通过天津I型全息干板记录两张散斑图，经处理后采用逐点分析法观察干涉条纹，结果如图5(a)所示。从图中可以看到，利用方法一同样无法看到任何干涉条纹，但方法二却可以看到清晰的干涉条纹。通过逐点分析法得到的微小偏移量为d为0.105 mm，然后代入公式计算得到玻璃折射率n为1.55。

(a)传统全息

数字全息实验获得的数字图像相关结果如图5(b)所示。其中，方法一的散斑相关图除了一个亮斑之外同样存在弥散点分布，测量得到的玻璃折射率n为1.31，误差较大；而方法二只有一个相关亮点，并未观察到任何弥散点，测量得到的玻璃折射率n为1.52，误差较小。

2.3 像面散斑法测量固体折射率

像面散斑法测量光路如图6所示，毛玻璃放在成像透镜前的两倍焦距物平面，而记录平面则放在透镜后的两倍焦距像平面，氦氖激光器发出的激光经扩束准直后，获得的平行光照射到毛玻璃形成散斑，散斑图像通过成像透镜和透明玻璃后被记录平面接收。

图6 像面散斑法的测量光路示意图

传统全息实验设定随机倾角θ为0.093 rad，经过相同的记录和处理过程，采用逐点分析法观察到的干涉条纹如图7(a)所示。结果同样表明，方法一获得的全息干板无法看到任何干涉条纹，而方法二的全息干板仍可以看到非常清晰的干涉条纹。经过测量计算，得到的微小偏移量d为0.095 mm，最终获得玻璃折射率n为1.52。

(a)传统全息

图7(b)是采用数字全息实验的数字图像相关结果。其中，方法一的散斑相关输出图仍然呈现明显的弥散斑分布，其玻璃折射率的测量值n为1.38，与参考值相差较大；而方法二还是一个自相关亮点，其测量得到的玻璃折射率n为1.50，与参考值接近。

表1 玻璃折射率的实验测量值

上述测量得到的玻璃折射率值示于表1。由此可见，对于方法一，轴向偏移量的影响使得前后曝光的两幅散斑图中难以找到相应的“散斑对”，故无论是用逐点分析法还是数字图像相关法，均无法准确获取散斑面内偏移量，使折射率的测量产生较大误差；而对于方法二，由几何光学可知，在倾斜角较小时垂直光轴放置和倾斜放置的透明玻璃产生的轴向偏移量几乎相互抵消，这使得记录平面两次采集到的散斑图仍然能找到相应的“散斑对”，从而能够获取准确的散斑面内偏移量。相比方法一，方法二极大地减小了轴向偏移量对测量结果的误差，但不会影响面内偏移量的测量结果，从而提高了测量精度，使计算结果更为精确。

3 结 语

根据透明固体的光学折射特性，对散斑法测量透明固体折射率遇到的关键问题进行剖析，并搭建了近场散斑、远场散斑和像面散斑三种光学测量系统，分别记录了经固体折射前后的两幅散斑图，并获得散斑面内微小偏移量，再根据理论公式计算出透明固体的折射率。本文采用了两种方法(现有方法和改进方法)，对厚度为3mm的固体玻璃折射率分别进行了传统全息和数字全息的实验对比研究，结果均表明改进方法具有误差小、精度高的优点。