例析正负相间数列的求和问题

山东省威海市第二中学 (264200) 燕 润

若数列的通项公式中含有(-1)n，则是一个正负相间的数列，关于它的求和问题需要对自然数n分为奇数或偶数等情况来讨论解决．但何时进行分类，还需根据题目的特点择机而行.下面从几类典型题目的评析入手，介绍其求解方案，希望能给读者朋友带来点收获．

一、求有限项的和

虽然是有限项，但不易采用逐一求出每一项的值后再求和，也不是简单的进行正负项处理能够解决的，大多情况下，都是需要通过特值验算找出特点，发现规律，抓住这些特点解题．

例1 已知函数f(n)=(-1)n+1n2(n∈N*)，且an=f(n)+f(n+1)，则a1+a2+a3+…+a100等于.

解析：由题意得a1+a2+a3+…+a100=12-22-22+32+32-42-42+52+…+992-1002-1002+1012=-(1+2)+(3+2)+…-(99+100)+(101+100)=-(1+2+…+99+100)+(2+3+…+100+101)=-1+101=100.

评注：通过对前100项和的分析发现每相邻两项都是平方差，通过应用公式化简再分类后发现是两组有规律的数分别求和，这就找到了解题的关键．由于是求特殊项的和，还需对特别的项如首项、末项的情况进行重点关注．

例2 数列{an}满足an+1+(-1)nan=2n-1，则{an}的前60项和为.

评注：由于本题的内在规律非常隐蔽，通过对三个连续的四项进行求值验算，终于发现其中隐含着一个等差数列，这样只需运用等差数列的求和公式解题就行了．

二、求前2n项和

由已知条件或递推公式求出通项公式是解决此类问题的前提．在求出数列的通项公式后，需要把握好前后两项和的特点，再找出规律解决问题．

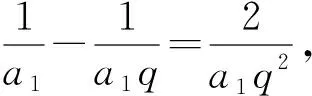
评注：首先根据已知条件求出了数列的通项公式，抓住题目中有2n项的特点，充分利用了(-1)n的特殊性，通过相邻两项的重新分组，找到了一个新数列的求和问题，这样完成解题就顺理成章．

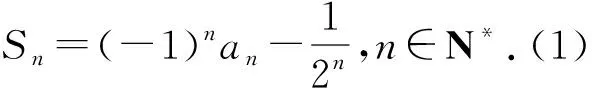
(2)根据{an}的关系式及递推式可求得a1=

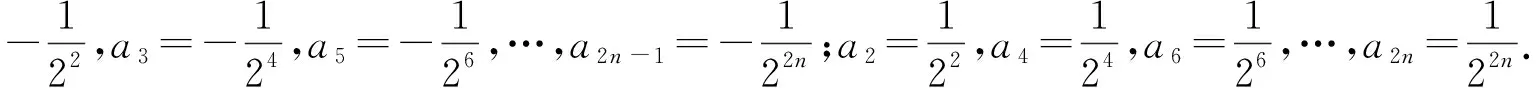
评注：本题也是求一个数列的前2n项和问题，但无法直接求出数列的通项公式，而通过求出-a2n-1+a2n关于n的表达式，然后再寻找其中规律成功地达到解题目的.找到相邻两项的关系式就是抓住了数列的前2n项求和问题的特点．

三、求前n项和

此类问题相比较求前2n项求和要复杂一些，其解法也可能与之不同.常规的方法是先对n为偶数时进行求和运算，然后再寻找n为奇数时它的前n-1项和与n为偶数时的关系得到表达式，再加上n项就是n为奇数时的表达式，最后再列出综合表达式．还可以是通过对n为偶数时及n为奇数时分别就其特点求出表达式．

例5 已知数列{an}的通项公式为an=(-1)n-1·(4n-3)，求它的前n项和Sn．

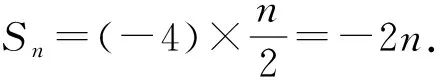
评注：由于题中所给的数列是一个正负相间的数列，每两项的符号规律是一致的，所以通过对几组两个相邻两项的和进行验证，就能发现规律，迅速解题．在此求和时是对自然数n分偶数、奇数讨论，分别列式求和，然后再合并呈现出前n项和Sn的表达式．

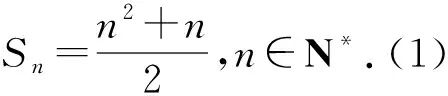
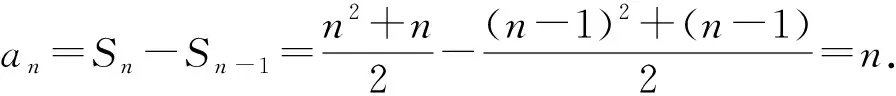
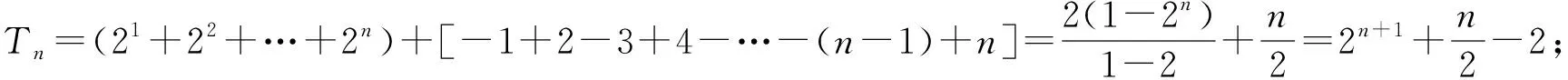
评注：此题采取的求解方法是先求出n为偶数时和的表达式，而当n为奇数时，则前n-1项和可仿照前面n为偶数时的求和，然后再加上最后的第n项就得到n为奇数时的表达式了．这个解题方法也是常用，而处理好n-1时与n时的关系是解题关键．