例析利用切线放缩法巧解函数不等式问题

广东省汕头市澄海华侨中学 (516007) 潘敬贞山东省滨州市邹平县黄山中学 (256200) 韩景岗广东省汕头市澄海中学 (515800) 陈焕涛

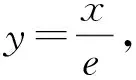
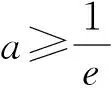
评注：本题的第(2)问利用切线放缩法进行放缩，问题的解答过程简洁，思路清晰、自然.但在函数y=ex-1的x=1处取切点，然后得切线方程y=x，从而可得不等式ex-1≥x成为本题利用切线放缩法解决问题的关键.

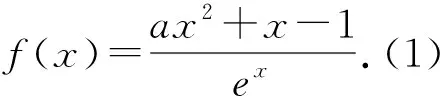
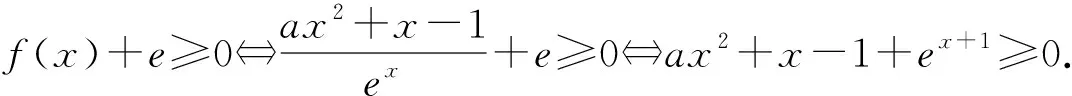
评注：本题的第(2)问的求解其关键是在函数y=ex+1的x=-1处取切点，然后得切线方程y=x+2，从而得不等式ex+1≥x+2，后面问题的解决就相对比较顺利.

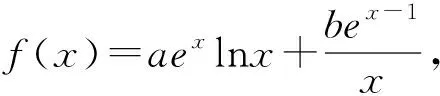
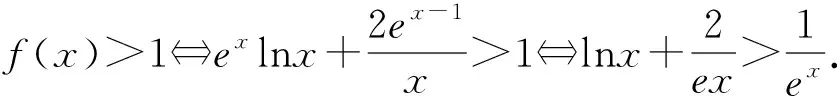
评注：当题目同时出现ex与lnx时，我们可以根据题意对ex或lnx进行切线放缩，本题的第(2)问就如此，既可以对ex进行切线放缩也可以对lnx进行切线放缩，都可以顺利解决问题.

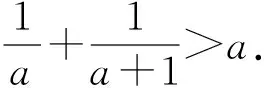
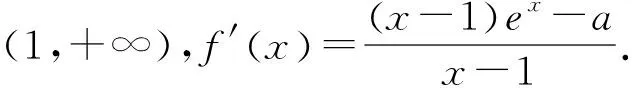
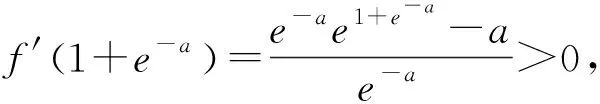
评注：本题的求解过程较为复杂，难度较大，但切线放缩法在简化解答过程，化解思维痛点等起到了很重要的作用.

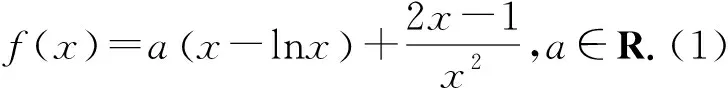
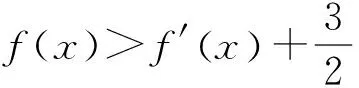
评注：本题的第(2)问利用切线放缩法可得到一个新的常规函数，然后再对其求最小值即可解决问题，但需要注意两次等号不能同时取到才保证了最后的等号取不到.

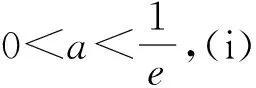
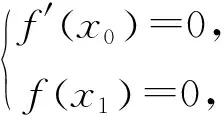
虽然说切线放缩法并不是万能，但是在解有关函数不等式问题时，当题目中的函数解析式含有ex或lnx的四则运算时，就可以考虑利用切线放缩法对问题进行处理、求解.利用切线放缩法解有关函数不等式问题可以有效突破解题智慧点，化解思维痛点，简化解题过程，提高解题效率.在利用切线放缩法对问题进行求解的过程中，其最关键是根据题意寻找到合适的切点，从而得出合适的切线，然后利用切线放缩法有效的将问题转化为较为常规、简单的问题进行解答，最后巧妙的将问题解决.因此，在日常学习过程中，要引导学生勤于思考，多动手实践，提升数学思维水平，积累数学活动经验等，对促进学生数学能力的提升，发展数学核心素养水平大有裨益.