用基本不等式求最值的破题五措施
2020-11-20甘肃省武威第十八中学733000高述文
甘肃省武威第十八中学 (733000) 高述文
在运用基本不等式求最值时,要注意使用“一正、二定、三相等”条件,而在寻找定值时,有时条件不够明显,常需要采用拆项、添项、变形、化简、换元等的技巧,这样化隐为显,使问题快速解决,本文通过举例分析、介绍几种常见的变换技巧,供参考.
1.适当拼凑:考察所给的表达式,看如何能通过进行适当的变形使之达到正确使用基本不等式的条件,完成解题目标.
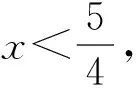
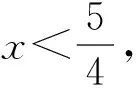
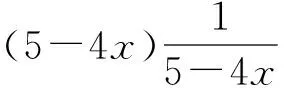
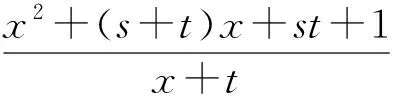
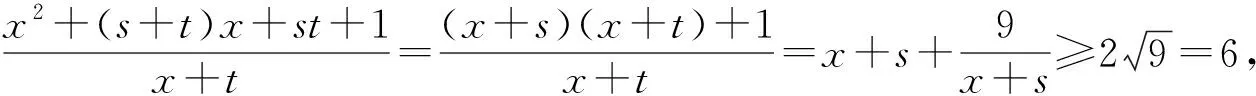
评注:本题容易出现误判,即没有抓住x+s>0进行正确的配凑,而是把x+t当着变元,使解题造成混乱得出错解或使解题无法进行下去.
2.配方配项:在题设中如果在分式的分子或分母中含有类似于二式三项式的,可通过及时配成关于父母(或分子)的二式三项式,这样后面的解题方法就能够显露出来了.
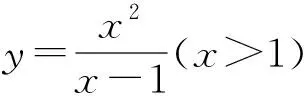

评注:在理解题意的基础上,通过对分子配方(关于分母的平方),构造出能使积为定值式子,这是找准了解题的切入点.
例4 若实数a、b满足ab-4a-b+1=0(a>1),求(a+1)(b+2)的最小值.
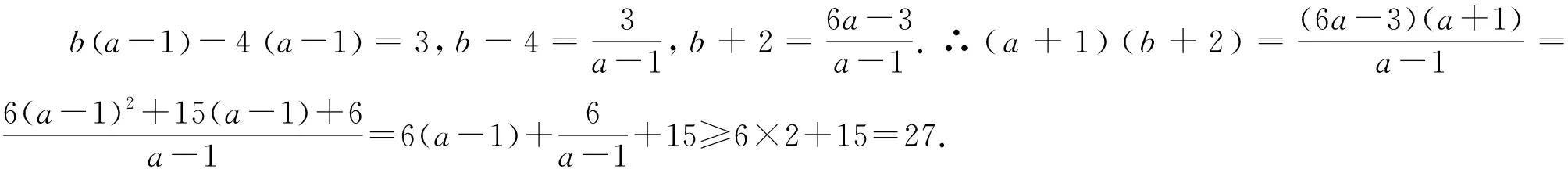
评注:本题中没有直接告诉相关的分式,通过挖掘已知条件,对条件等式和欲求的式子进行重新整理,再合理配方,构造出可用均值不等式求解式子,化解了问题的难点.
3.及时相除:在一些分式求最值问题中,通过对分式的分子、分母同时除一个适当的式子,可以发现能使用基本不等式解题的契机.
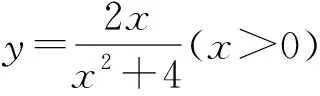

评注:通过分子、分母同除以x,使分子为常数(必须是),同时也能使此时分母的积为定值,这样就达到了使用基本不等式解题的条件了.
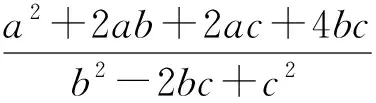
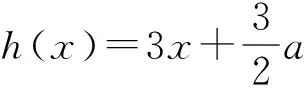
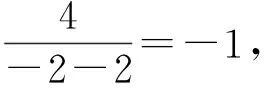
评注:通过对题目的深入研究,挖掘了其中隐含的关系,即一个乘积式的符合确定,再整体思考、整体变形配凑,使问题终于得到解决,这是科学有序的思维品质的体现.
4.连续放缩:在一些相对复杂的式子中,经过一次放缩可能达不到目的,可以再一次进行放缩变换,直到符合要求,这里必须注意连续放缩所需的相等条件是一致的.
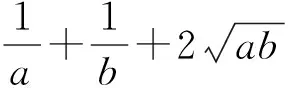
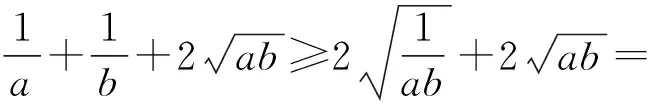
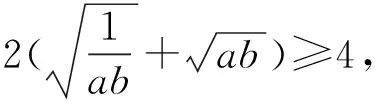
评注:本题虽然用了基本不等式放缩两次,但由于等号成立的条件是一样的且缩小的方向一致,故而并不影响最小值的确定,如果等号成立的条件不一样或方向不一致,则得出的结果肯定是错误的,必须引起重视.
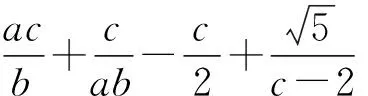
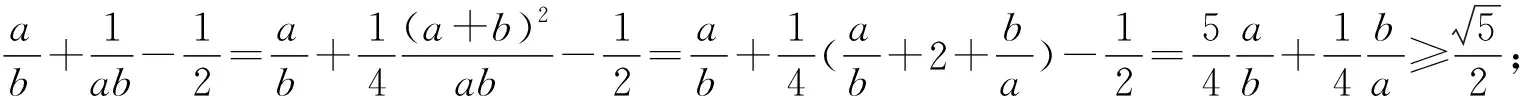
评注:本题中的字母较多,条件也不少,如何适当使用是解题关键,而本解法中分两次运用基本不等式求解,方法独到,简便合理.
5.灵活换元:抓住题设中的某些特殊结构进行类比联想,再通过换元对原式进行改造,可发现破题的机会,完成解题任务.
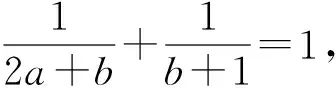
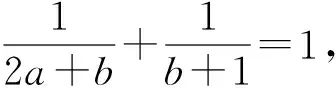
评注:若在题设中含有两个正项和为1(或某个特定的值),可以选用三角换元,这样就可以利用三角函数的知识进行变形求解,达到解题目的.
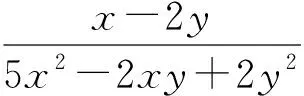

评注:本题通过对所给的式子进行变形,然后对其中的特定结构进行换元处理,用新变量替换原来的变量,揭露了隐含的关系,为顺利解题创造了条件.
上面讲述了使用基本不等式求最值的五个破题措施,常见而实用,如果我们在教学中能够让学生掌握并领会了这些解题方法,那么学生在应试时遇到这些题目可能就信心满满了.
