源自例题 现于真题 探究“新题”*

福建省龙岩市高级中学 (364000) 谢盛富

教材中的例习题凝聚着专家和编者们的智慧结晶，它们具有典型性、代表性和示范性，隐藏了解题思路、方法、背景和结论等.因此，对教材的开发与利用显得极其重要，通过拓展延伸，能丰富教师的知识体系，培养学生的探究能力、创新能力，提高数学素养.笔者以文[1]第92页例2(Ⅰ)为例，进行“二次开发”出一系列变式探究.

例题已知O为原点，直线y=x-2与抛物线y2=2x相交于点A，B.(Ⅰ)求证：OA⊥OB；(Ⅱ)求|AB|的长.

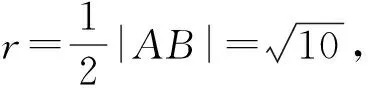
思考1：本小题简单、通俗易懂，似乎没有特别之处，然想想，本题可逆吗？换言之，能由“OA⊥OB”得到“直线方程为y=x-2”吗？直线唯一吗？

探究1 已知O为原点，一直线l与抛物线y2=2x相交于点A，B.探究：若OA⊥OB，试求直线l的方程.

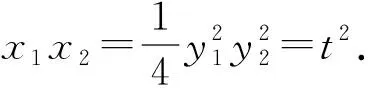
结论1O为原点，直线l与抛物线y2=2px(p>0)相交于A，B两点.若OA⊥OB，则直线l恒过定点(2p,0).反之亦成立.

思考2：直角顶点一定在原点O处吗？抛物线上有无其它点C满足“CA⊥CB”？

探究2 直线y=x-2与抛物线y2=2x相交于点A，B.试探究：在抛物线上是否存在一点C(异于原点O)，满足CA⊥CB？请说明理由.

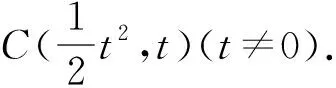
结论2 直线l与抛物线y2=2px(p>0)相交于A，B两点，点C在抛物线上，则满足CA⊥CB的点C有4个.

思考3：直角顶点能在抛物线外的某点M吗？即仍然有MA⊥MB吗？

探究3 过抛物线y2=2x外一点M作两条互相垂直的直线，且均与抛物线C相切，切点分别为A，B，求证点M必在某条定直线上，并求此定直线方程.

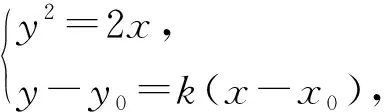
一些问题直指关键。北京市人大内务司法委员会主任委员陈永提问,目前医养衔接还存在部门各自为政现象,如何加强统筹有效推进医养结合?北京市卫生健康委主任雷海潮则坦诚回应：北京市级层面已建立市老龄委员会,成员单位已达到55家,为更好履行老龄委员会办公室的有关职责,我们还建议设立相应的内设机构。

思考4：探究3中的直线AB过某一定点吗？2019年全国新课标Ⅲ卷理21、文21恰好考查了，背景是阿基米德三角形，这正是反映了高考题来源于教材例习题.事实上，教材例习题、往年高考题和一些优秀数学名题都可能成为某年的高考题，回归课本，研磨真题，一题多变，多题归一，值得师生们重视.

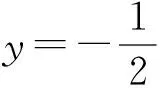
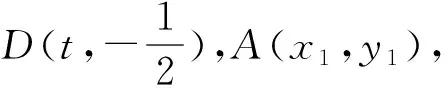
结论3 过抛物线外一点M作抛物线的两条切线，若两条切线互相垂直，则点M必在准线上.反之也成立.

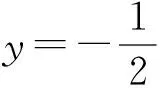
探究5 已知抛物线x2=2y，过直线y=-1上的动点D作抛物线的两条切线，切点分别是A，B.

(Ⅰ)证明：直线AB过定点；(Ⅱ)记两条切线DA，DB的斜率分别为k1，k2，求证：k1k2为定值.

解析：设点D(t,-1)，仿探究4的证明可得直线AB的方程为tx-y+1=0，直线AB过定点(0,1)，k1k2=-2(定值).

结论4 已知抛物线x2=2py(p>0)，过直线y=m(m<0)上一点M作抛物线C的两条切线，则切点弦所在直线必过定点(0,-m)，且两切线的斜率之积为定值2pm.

思考6：探究1的条件“垂直”改成角度为定值，直线l是否还会恒过定点？

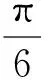
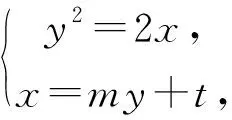
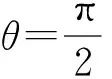
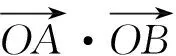
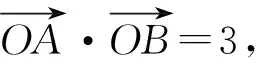
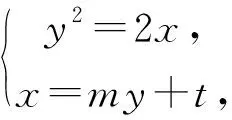
为什么会出现t=3和t=-1两种情况呢？它们各代表什么含义？结合图形分析可知，当t=3时，直线l与抛物线的交点在x轴两侧；当t=-1时，直线l与抛物线的交点在x轴同侧.因此，要使直线l恒过定点，必须在题中增加条件“A，B在x轴两侧”或“A，B在x轴同侧”，此时直线l对应恒过定点(3,0)和(-1,0).

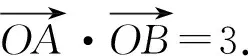
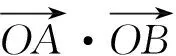
可见，紧扣教材，立足学情，充分发挥例习题的功能，抓住时机有针对性的启发，让学生尽可能提出不同的想法，激活他们参与变式探究的乐趣，体验数学的魅力而不是冰冷，提升思维的广度和深度，提高学习数学的积极性和主动性，抓住问题变化的核心，经历问题的层层递进，深度探究，能全面提高学生在各方面的综合能力，解决问题应做到更好、更简、更巧，达到提升数学核心素养的目的.