共轴反转型生物反应器内流场数值模拟与性能分析

2020-11-18杨光王沫然

化工学报 2020年11期

杨光，王沫然

（清华大学工程力学系，北京100084）

引言

塑料作为人们生活中最常用材料已经深入人们生活的方方面面，但是，塑料制品的不易回收利用及难以自然降解带来了严重的白色污染问题[1-4]。开发和使用生物降解塑料是一种行之有效的解决方案。然而，目前生物降解塑料价格过高，如何降低生物降解塑料的生产成本成为了解决白色污染的关键。在生物降解塑料的生产过程中，需要在反应器中通入生物发酵所需氧气并排出二氧化碳，同时保持生物发酵所需的最佳温度。传统的生物反应器往往存在氧传质能力不足、能耗过大等问题，这些问题不仅造成能源浪费、产物成本过高，同时也会影响发酵过程中的细菌代谢，降低发酵产量，造成了生物降解塑料成本居高不下。因此，对生物反应器进行传热传质的优化，成为降低生物降解塑料成本的关键。

传统通气式机械搅拌反应器具有一个或多个桨叶，如图1 所示，利用桨叶旋转形成涡流，对气流进行打散、分散及混合。前人对反应器的优化设计主要围绕多个不同类型桨叶的不同组合形式及尺寸和间距等进行研究[5-13]，而对运转条件的分析较少，即便有所涉及也是针对桨叶同向旋转条件，而对桨叶旋转反向情况的研究未见报道。简单力学分析可知，桨叶反转能够在两桨叶之间形成强烈的剪切流动，可强化湍流传质，进而降低生物反应器的能耗，但具体效果尚需验证。

图1 典型机械搅拌式反应器设计Fig.1 Typical design of stirred tank reactor

常规实验手段进行流场分析价格昂贵，受限于实验条件，不易进行工业放大。数值模拟能够有效进行流场定量分析，且不受实际物理时空限制。因此，数值仿真已经成为生物反应器研究中降低实验成本[13-14]、优化反应器设计[13,15-19]、进行工业反应器放大[12,20-21]的重要手段。然而，由于反应器中存在气液两相和搅拌等复杂流动行为，当前对通气式搅拌器内气液两相流动模拟仍存在较大挑战，特别是两相流体的相间作用力模型，其准确性对模拟结果有较大影响。Deen[22]指出曳力模型的选择对双流体模型的模拟精度有较大影响，并在模拟中采用了Ishii 和Zuber 模型[23], 两相湍流模型使用Sato 和Sekoguchi模型[24]。Liew 等[25]比较了不同曳力模型在鼓泡塔中的两相流动模拟，结果显示不同曳力模型结果相差不大，两相湍流模型采用了Simonin 和Viollet 模型[26]。Lou 等[27]比较了五种不同曳力模型对气泡羽流模拟的影响，结果显示Kolev模型[28]明显优于其他模型，考虑湍流扩散力与否也有较大影响。可以看出，不同学者对两相相互作用模型的选取不完全相同。对两相反应器的模拟优化，文献中通常缺乏详细说明其计算所采用的模型及相关参数[17,29-31]，缺少模型及参数验证，影响了优化结果的可信性。

针对以上问题，为了能可靠地对生物反应器进行模拟优化，本文首先对气液模拟数值模型进行多角度验证，然后对本文提出的双桨叶共轴反转反应器内不同运行参数下的流场进行了模拟分析，从而对反应器的工程应用提出优化建议。

1 数学模型

本文采用双流体模型——欧拉-欧拉模型描述下的两相流动，采用动网格方法求解旋转机械。双流体模型将连续相和离散相都近似为连续流体，对连续相和离散相采用各自的动量方程和能量方程描述，并在两相间考虑质量、动量及能量的相互交换。双流体模型忽略了离散相的离散特质，对离散相采取均化处理[32]。

在双流体模型中，仅引入控制域方程是不够的，准确描述还需要补充恰当的动量和能量交换模型，例如曳力模型、升力模型、湍流分散力模型及气泡诱导湍流模型等。这些模型的选取对模拟准确度有较大影响。前人对不同模型进行过分析比较[16,27,32-35]，本文将给出所用模型的细节及选取依据。

1.1 控制方程

在双流体模型中，离散相和连续相各自满足连续方程和动量方程，若先考虑最佳温度下的流动及传质行为，忽略温度影响，则先忽略能量方程。由于本文不直接考虑化学反应，连续方程中可忽略源项和组分输运项，则连续方程可简写为：

其中，下角标l、g分别表示液相和气相。ρi表示第i 相密度，ui表示第i 相速度。而φi表示第i 相的体积分数，即∑φi= 1。动量方程可写为：

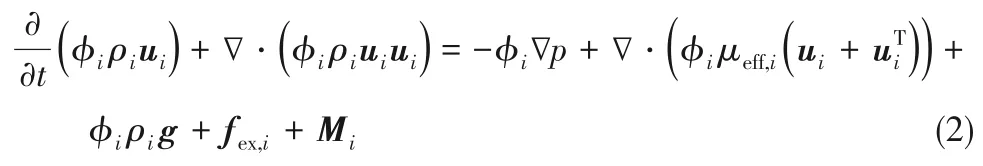
其中，p 表示两相共同的压力场，φiρig 表示该相所受的重力，fex,i表示该相所受到外力，如非惯性系中受到的离心力及科里奥利力等。Mi表示两相之间由于相对运动和湍流等因素造成的动量交换，μeff,i表示由湍流等引起的等效黏度，即μeff,i= μi+ μt,i，其中μi表示该相的动力黏度，μt,i表示湍流黏性系数，由湍流模型决定，本文采用标准k -ε模型模拟。

1.2 相间作用力

相间作用力是影响双流体模型预测准确性的最重要因素。根据前人研究，虚拟体积力主要描述气泡加速时的等效力，这一作用对结果准确性影响较小。因此本文主要考虑了文献中常见的其他几种相间作用力，包括曳力、升力和湍流分散力[22,27,35]等，即：

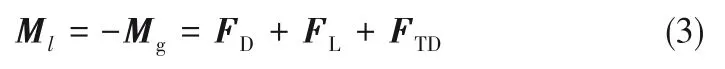
曳力表征了气泡运动过程中的阻力，一般可以写为：

其中，db为气泡直径，CD为曳力系数。本文采用Kolev 模型确定曳力系数[28]，在Ansys 中称为通用曳力模型(universal drag law)，该模型广泛适用于各种气泡流，包括非球形气泡等气泡变形情况下的气泡曳力计算。

同时，气泡在液体中运动时，还会受到连续相速度梯度影响产生的Saffman 力和气泡在连续相旋转运动时受到的Magnus力。在双流体模型中，一般用升力来统一描述：

其中，CL为升力系数。本文使用文献中通行的变系数Tomiyama 模型，该模型可较好地描述不同变形区的气泡行为[16,35-36]。

湍流分散力FTD表示由湍流脉动造成气泡运动使气泡分散的力。本文采用RANS 模型，对速度进行时间平均，曳力项可以表示为：

1.3 两相湍流模型

连续相采用标准k-ε 模型，并加入源项来描述气泡对连续相湍动能以及湍动能耗散率的影响。标准k-ε 模型是一个典型的双方程模型，该模型通过湍动能及湍动能耗散率方程对湍流黏性系数进行封闭，是工程中常用的经典湍流模型。

连续相(液相)的湍动能方程：

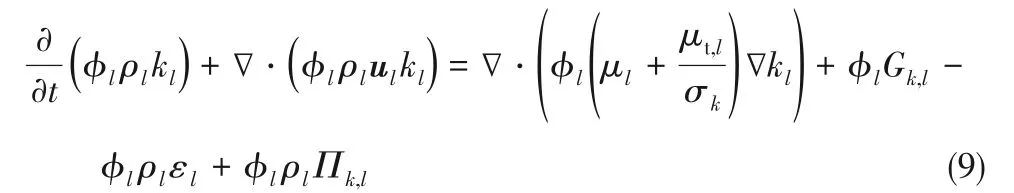
湍动能耗散率方程：

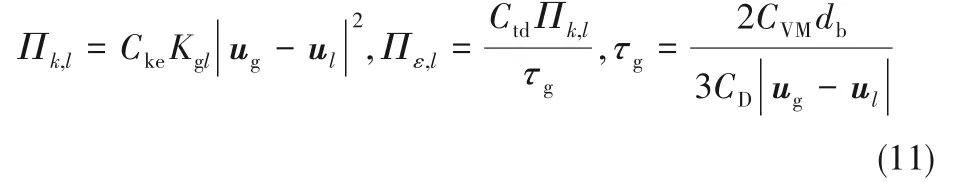
而离散相的湍流运动黏度与连续相一致。其中模型参数取值见表1。

表1 湍流模型参数数值Table 1 Coefficient value of turbulent model

2 数值方法验证

2.1 两相模型验证

前面提到两相模型对两相流场模拟结果影响显著，因此需要对选取的两相模型进行严格验证，以保证结果正确性。本文分别模拟了气泡羽流与鼓泡塔两相流的流场，并与实验数据做了对比验证。

气泡羽流模拟的几何参数参考了Castillejos 和Brimacombe 实验[39]的设置，边界条件如图2 所示,气泡大小依据实验中测量结果设置为2.65 mm。模拟所用网格数2万～10万，并验证了模拟结果的网格无关性。数值仿真在软件平台Ansys Fluent 18.2 上完成,模拟结果如图3和图4所示。

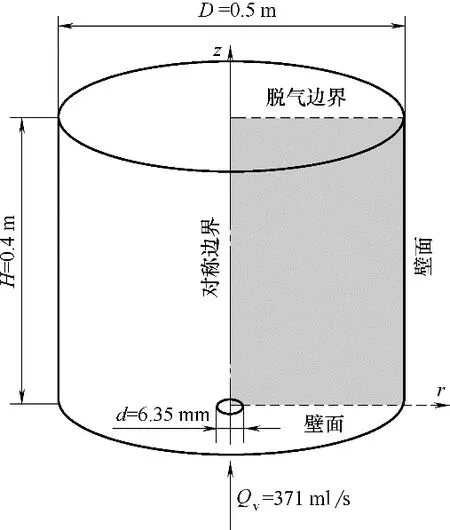
图2 求解问题几何与轴对称近似下边界条件设置Fig.2 Size and structure of bubble plume problem and boundary condition of axisymmetric situation

图3显示了气体体积分数的云图，如图所示，大量气体集中在对称轴附近，少量气体靠近壁面区域，这与文献中的结果是一致的。图4 定量比较了文献中常用的Schiller-Naumann 模型[22,27,35,40]和本文采用的Kolev 模型对气体体积分数和气体速度分布的影响，两者主要的差异在气体体积分数的预测上。普遍认为Schiller-Naumann 模型可以描述单一气泡的曳力模型，当气体体积分数较大时或在气泡聚集的区域误差较大，因此本文采用了更为准确的Kolev模型。

图3 气泡羽流气体体积分布情况Fig.3 Gas volume fraction distribution of bubble plume

进一步，本文比较了气体体积分数沿径向的分布。图5 对比了无量纲气体体积分数沿径向的变化，无量纲化的体积分数计算如下：

其中φN和rN表示无量纲化的值。只沿径向进行了无量纲化，即此时φ 只是r 的函数。rφ2表示φ(r)最大值一半所处的位置。

文献一般认为无量纲气体体积分数近似服从高斯分布[41-42]，即图中Iguchi等(1995)[42]所示。

Castillejos 和Brimacombe 认为分布指数应该为2.4而不是2，即图中Castillejos和Brimacombe(1987)[39]所示。

结果表明，两条曲线差异不大，且本文模拟结果与实验结果基本一致。在位置较低(5 cm)处结果偏差较为明显，原因可能是由于入口附近流动变化较为剧烈，当前模型难以准确捕捉。

为了验证轴对称假设的可靠性,本文还进行了对应的三维模拟。结果如图6 所示，可以看到二维轴对称模拟与三维模拟结果一致，表明二维轴对称简化模拟结果可靠。

图4 两种曳力模型对比：气体体积分数（a）及气体速度（b）沿中心分布Fig.4 Comparison of two drag model:gas volume fraction(a)and gas velocity(b)

图5 气体体积分数沿径向的分布Fig.5 Gas volume fraction along radial direction

图6 二维轴对称模拟与三维模拟对比：气体体积分数（a）及气体速度（b）沿中心分布Fig.6 Comparison of 2D axial-symmetric result and 3D result:gas volume fraction(a)and gas velocity(b)

尽管气泡羽流能够一定程度上反映两相气泡的相互作用，但在气泡羽流问题中气相主体远离壁面，依然不足以反映真实反应器几何结构对两相流的影响。为此，本文进一步选取了鼓泡塔两相流问题验证模型的正确性。选取的几何尺寸与边界条件如图7所示。

长方体鼓泡塔高0.45 m，底面0.15 m×0.15 m。底面中心开有0.03 m×0.03 m 的通气口，通气速度为0.1225 m/s。初始时鼓泡塔装满水。底部入口设为给定速度边界，连续相（水）速度设为0，体积分数设为0；离散相（气）速度根据真实通气速度确定，设为均匀通气，体积分数为1。壁面均为静止壁面，采用标准壁函数。顶部为脱气边界，即对连续相为滑移边界，对离散相为气体消失边界。气泡大小参照文献[35]设为4 mm。气体体积分数云图与液体速度矢量图如图8 所示。结果表明气体上升时非直线上升，所形成的云图也并非对称，气体分布在反应器中有一定扭转。从速度矢量图来看，可以明显看到右下和左上的两个涡的结构，这与前人的模拟结果[22,35]是一致的。

图7 鼓泡塔几何尺寸与边界条件示意图Fig.7 Geometry and boundary condition of bubble column

图9显示了选取截面上的气相与液相的平均速度分布，并与实验数据做了对比。由于这一流动一直处于非稳定状态，一般采用时间平均的方法计算平均速度，定义为：

图8 中心截面处51.5 s时气体体积分数云图（a）和液体速度矢量图（b）Fig.8 Gas volume fraction(a)and liquid velocity vector map(b)of center section at 51.5 s

2.2 两相搅拌模型验证

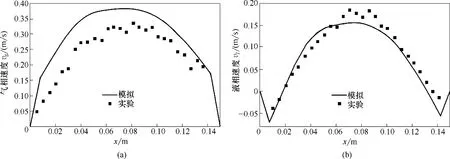
图9 高度z/H=0.63，y=0.075 m截面上气相（a）与液相（b）速度沿x方向变化Fig.9 Velocity of gas(a)and liquid(b)along x axis at height z/H=0.63 and depth y=0.075 m

图10 两相搅拌体系验证算例几何结构Fig.10 Structure of two-phase stirred tank benchmark

由于新设计中涉及到桨叶搅拌，因此还需对仿真所用的两相搅拌模型进行验证。为了与实验结果对比，两相搅拌体系计算几何参考了实验数据，如图10 所示，反应器直径T=0.222 m，四周均匀分布有4个竖挡板，板宽B=T/10，桨叶为Rushton桨，直径D=T/3，位于反应器中央，即C=T/2，叶片高度l=D/4，宽度w=D/4。气体分布器设置于桨叶下方，半径d=0.16T，距底部高度h=T/16。所有设置与文献[22]中模拟设置一致。由于Deen[22]的实验部分是反应器圆弧形底面(dished bottom)，因此这一设置比实验气体分布器高度略低（实验部分气体分布器高度为T/10）。通气量为7.2×10-5m3/s，即入口气体速度约0.07 m/s，转速为360 r/min，气泡直径为4 mm。采用滑移网格方法模拟，计算至稳态后，采用时间加权的方式，与实验结果进行了对比。

气体体积分数云图如图11所示，在桨叶的后部有气体体积分数很高的区域。这是由于在当前的运行状态下，反应器处在气泛状态，大量气体聚集在桨叶背面的低压区内，形成气穴[22,43]。

为了进一步进行定量对比，选取了0°、10°、20°、30°、40°、50°六个平面上的速度进行空间加权平均：

图11 两相旋转机械内气体体积分数云图Fig.11 Gas volume fraction of two-phase stirred tank reactor

在此基础上再进行时间平均，定义同式(15)。图12 比较了r/T=0.185 处液相速度分布情况（反应器正中央位于z=0，r=0 处）。结果表明，本文模拟的液相速度与实验结果吻合良好。当网格数为21 万时，在高度坐标2附近出现了一处明显的不连续点，这可能是由于在时间平均和空间平均过程中引入了数值误差，增加网格数后不连续点消失。与Deen[22]的模拟结果相比，由于Deen 所使用的两相模型过于简单，导致其对液相轴向速度在z=3 附近出现了明显的偏离，而本文所使用的模型可以改善预测精度，与实验数据符合。

图13 显示了两相流中气相的平均径向速度和轴向速度结果，并与实验结果作了对比，径向速度与实验吻合较好，而轴向速度预测存在较大误差。即便如此，轴向速度预测可以基本定性地反映速度的变化趋势，能够预测出实际过程中出现的两个速度峰和速度谷，且本文结果在定量上优于Deen[22]模拟结果。误差产生原因主要是两相模型导致的。在搅拌式反应器中，气体存在更为复杂的破碎聚并以及变形的行为[44]。因此，单一气泡尺寸的双流体模型在这一问题的预测上会产生较大误差，可以在今后工作中继续探索更精确的两相模型。

图12 液相径向速度(a)与轴向速度(b)Fig.12 Radial velocity(a)and axial velocity(b)of liquid phase

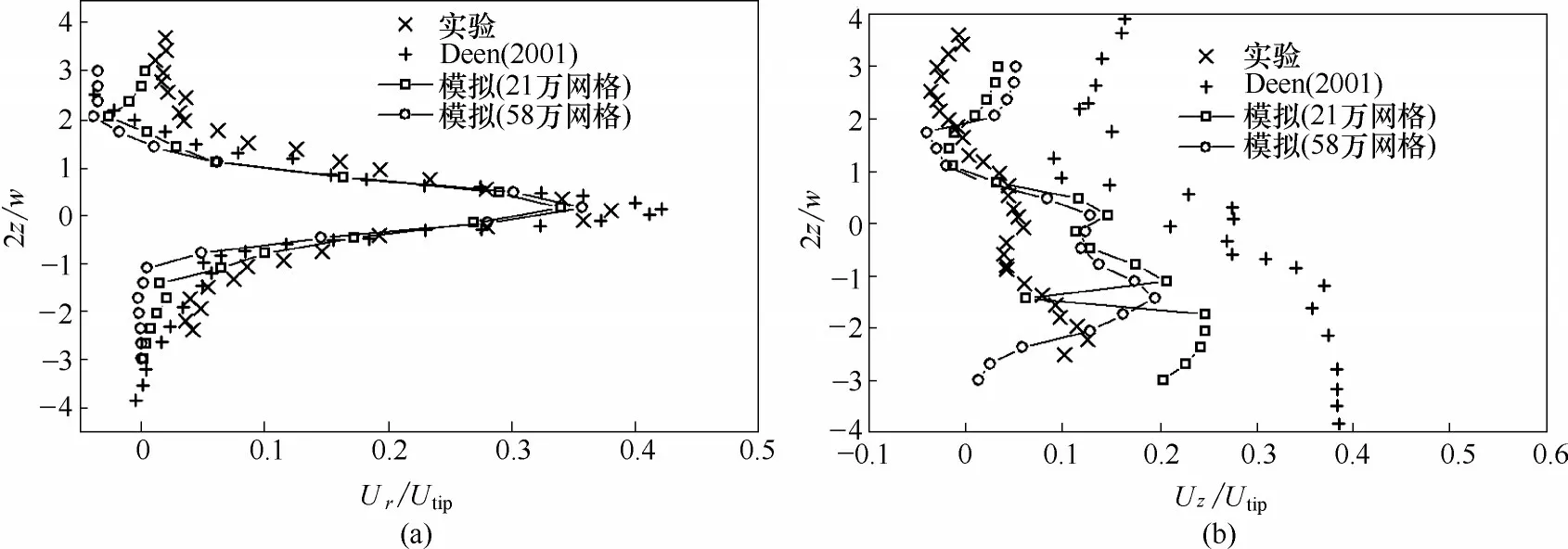
图13 气相径向速度(a)与轴向速度(b)Fig.13 Radial velocity(a)and axial velocity(b)of gas phase

3 共轴反转反应器流场分析

共轴反转原本是航空领域中的一种经典布局，它是通过将两个螺旋桨布置在同一根轴上，一个螺旋桨顺时针转动，另一个螺旋桨逆时针转动，以减小乃至消除由于桨叶旋转而作用在航空器上的力矩。并且，良好设计的共轴反转系统能够减弱叶尖脱落的涡结构，能够提升推进效率6%～16%[45]。但是在反应器领域，一般两个桨叶间距都大于桨叶直径，使得两个桨叶的流动不会相互干扰。因此，对于多桨叶组合的设计都是同向转动的，没有共轴反转的设计及研究。本文将通过数值仿真对共轴反转反应器在完全分散状况下的运行性能进行研究，并与相同构造的同转反应器进行对比，以比较两种反应器设计的优劣。

3.1 模型建立与网格划分

如图14所示，本文提出的共轴反转反应器与传统的多桨叶反应器主体结构一致。主要参数为：C=D=T/3，S=1.2D，H=1.2T，B=T/10。有四块挡板，桨叶是Rushton 桨。值得注意的是，两个桨叶的间距虽然大于一般文献的推荐值1[43]，但也有研究指出，对于Rushton 桨而言，这个值一般推荐为2[46]。运行条件为不通气或通气量为8.8×10-5m3/s，转速为200 r/min。根据Taghavi 等[14]推荐的经验关联式，在这一转速和通气条件下，反应器处在完全分散的状态。这种状态下两相流动由桨叶主导，因此容易观察到由于桨叶的操作方式不同带来的反应器性能差异。

图14 两桨叶反应器几何结构Fig.14 Structure of dual turbine stirred tank benchmark

3.2 单相情况

图15 显示了共轴反转反应器和共轴同转反应器的流场存在显著差异。共轴同转反应器中下面桨叶产生的涡上半部分与上面桨叶产生的涡下半部分发生了融合，因此，反应器中间部分的流线表现出了严重的杂乱无章。由于两个涡发生了融合，也意味着这种情况下轴向的混合会有一定的提升。而共轴反转反应器的两个桨则显著地显示出了两个独立的涡结构。上下两个桨叶所形成的流动较为独立。

很多文献[43,47]都指出,机械搅拌反应器内的等效传质系数KLa∝P0.3～0.8，即功率越大传质能力越强，功率是反映反应器传质能力的重要指标。从功率消耗情况来看（图16），共轴反转反应器在相同操作模式下消耗更大的功率，而共轴同转反应器的功率较小，功率小于两个单一桨叶功率的和。其原因就在于共轴同转反应器在两个桨叶较为靠近时，两个桨叶流动产生的涡流发生了融合，因此，消耗功率较低，这对传质是不利的。为了改变这一情况，增大了能量输入，文献[43,46]中对两个桨叶的距离有明确要求。而共轴反转反应器在相同的几何构型下实现了这一点，即在桨叶间距离不增加的情况下，通过反转来避免两个桨叶形成的流动发生涡融合的现象。因此其输入能量更多，功率更大，具有更强的传质能力。

图15 单相时反应器流线图：转动方向相反（a）和转动方向相同（b）Fig.15 Streamline of single phase reactor:contrarotating(a)and corotating(b)

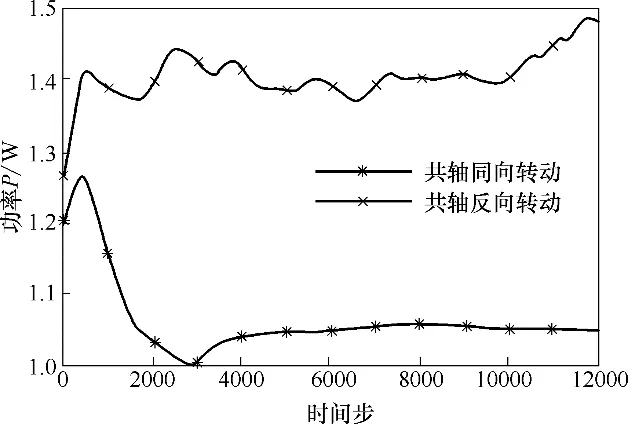
图16 单相情况功率随时间步变化情况Fig.16 Power consumption of single phase at different time step

3.3 两相情况

对于底部通气的两相流情况，图17展示了对称轴截面上的速度分布及云图，可以看到，在气体作用下，液相出现了更为强烈的对流。结果表明，虽然气液两相情况下共轴反转也发生了涡融合的现象，但涡的位置较同转情况更为分散，这有利于能量的输入和耗散。

由于两个反应器功率不同，比较整体气含率和整体传质系数没有意义。因此，这里计算了两个反应器的RPD（相对功率准数）值，即：同转时，RPD=0.810；反转时，RPD=0.818。RPD 值均在0.8 以上，桨叶功率下降较小，而且反转时功率下降较低。根据气体体积分数云图显示,虽然中心气体分布密集,但中心的气体体积分数均在0.4以下,且桨叶附近也未形成严重的气穴。因此，两种工况均在完全分散状态。同时，本文还比较了图17中所示的气体体积分数云图中三个平面的气体体积分数标准差来衡量气体分布情况，同转时为0.2，反转时为0.17。因此，同转情况下气体发生了较为明显的中央附近聚集现象，而反转时气体分布更为均匀，即此时RPD值也更大。从气体体积平均气含率来看，反转（0.00896）的情况也大于同转（0.00762）。

与单相时相同，由于涡融合的出现，两个桨叶有最小距离限制。因此，如果在多桨叶反应器设计中引入数量过多的桨叶将会造成反应器高径比过大，从而导致通气功率需求增大。而如果桨叶过于分散则又会导致桨叶使用组合的意义丧失，且限制了体积平均功率的提升。利用共轴反转的操作则使得较为密集的桨叶构型成为可能，能够有效地提高体积平均功率，使得流场的能量密度更大，湍流脉动更强，促进传热传质。