甲烷爆炸对建筑物内外压力场分布的影响

李玉星，尹渊博，王雅真，刘翠伟

（1 中国石油大学（华东）山东省油气储运安全省级重点实验室，山东青岛266580； 2 中国石化青岛安全工程研究院，山东青岛266580； 3 中国石油大学（华东）储运与建筑工程学院，山东青岛266580）

引 言

近年来，管道泄漏爆燃事故频繁发生，造成大量人员伤亡和财产损失。当泄漏的甲烷气体浓度处于爆炸极限内，便存在爆炸的危险，因此需要首先明确甲烷气体的爆炸极限。Vanderstraeten 等[1-5]研究发现，甲烷气体在20℃，100 kPa 下的爆炸下限为4.6%±0.3%，上限15.8%±0.4%，但这一范围在不同温度压力条件下会发生变化。Cui 等[6]测量了甲烷-空气混合物在低初始温度(113 K 以下)和高压力下的爆炸特性，燃烧持续时间和火焰发展持续时间均随初始压力的增大而增大，随初始温度的升高而减小。Huang 等[7]研究表明甲烷在高压下的燃烧下限略有降低，超过3 MPa 后燃烧上限显著提高。Zheng 等[8]研究了存在浓度梯度(既非均匀混合)的甲烷-空气混合物的燃烧，其结果表明，组分浓度梯度会使燃烧速度降低。

甲烷空气预混气体一旦发生爆炸，会产生极其严重的危害，为了能更好的减小危害程度，必须对其可能产生的后果进行分析。目前对于气体爆炸超压后果的计算通常使用TNT 当量模型[9]和TNO 多能模型[10]，前者是将蒸气云爆炸的能量当量转换为TNT炸药的质量，但TNT是理想爆源，导致该方法误差较大。后者是将不同燃烧速率下的无量纲爆炸超压与无量纲距离绘制成曲线图查图使用，使用时受人为的主观影响很强，结果可信度并不高。Dobashi 等[11]对此进行了改进，得到了适用于气体爆炸压力场的计算公式。为更好的揭示气体爆炸规律，部分学者对爆炸压力场及超压冲击波的传播做了深入研究：Bao等[12]通过设置不同体积和浓度的预混甲烷/空气气云爆炸实验研究了开敞空间内甲烷爆炸的相关特性。Gostintsev 等[13]基于自相似火焰传播理论，提出了具有自发火焰不稳定性的火焰传播半经验公式。Kim[14]提出无约束气体爆炸具有自相似传播特征，并在研究中对Gostintsev 等[13]提出的公式做出了修正。Strehlow 等[15]利用火焰传播的恒定速度和加速度来分析由球形火焰产生的爆炸波。Li 等[16]分析了城市井盖甲烷气体爆炸超压变化规律。Huang 等[17]实验研究发现最大爆炸超压与最大燃烧速度呈对数函数关系。

上述学者的研究工作大多是面向无约束条件下的爆炸工况，但实际生产过程中面对的往往是存在障碍物的情况。当存在障碍物时，由于在传播过程中气体受到阻塞，火焰在通过障碍物时其锋面扭曲褶皱形成湍流旋涡，部分学者针对障碍物存在条件下的爆炸进行了研究。Ciccarelli 等[18]研究发现，障碍物存在情况下冲击波会限制最终的燃烧速度。Harrison等[19]通过实验证明，爆炸火焰的传播速度和超压随障碍物间距的增大出现先增加后减小的趋势。Wang等[20]和Hall等[21]得出相似结论。不同形状的障碍物(如圆柱形、三角形、立方体、菱形和平板形等)，都可以加速火焰的传播[22]，Ibrahim 等[23]分析了不同形状的障碍物对爆炸结果的影响，其实验结果表明，板形障碍物所产生的超压最高，而圆柱形障碍物对超压的影响最低。Xu 等[24]通过实验同样得出类似的结论。

目前对于无约束条件下甲烷空气混合气体的燃烧过程以及爆炸超压的研究已成体系，对于约束条件下，气体预混爆炸在障碍物周围产生压力场的研究也取得了一定的进展，但目前尚未有对于气体爆炸在障碍物内部产生压力场的研究，因此本文在经实验数据修正的无约束预混爆炸模型的基础上，建立三维约束预混气体爆炸模型，分析了障碍物高度和宽度对障碍物外部压力场分布的影响，与之前相关文献作比较验证该模型与求解方法的正确性，在此基础上研究了气体预混爆炸在障碍物内部产生压力场的分布规律，给出了实际爆炸发生时相对安全的位置。

1 理论分析

1.1 伤害判定准则

目前较为常用的爆炸伤害判断标准主要有超压准则、冲量准则以及二者结合使用的方法。超压准则认为，只有当爆炸冲击波超压大于或等于某一临界值时，才会对目标造成一定的伤害。否则，爆炸冲击波不会对目标造成伤害。冲量准则认为，只有当作用于目标的爆炸波冲量达到某一临界值时才会引起伤害[25]。实践表明，不同的爆炸源有不同的爆炸波形，同样冲量值产生的破坏作用也可能会显著不同[26]。文章选用超压准则作为衡量标准展开，表1 和表2 展示了超压波对人体的伤害和对建筑物的破坏。

表1 冲击波超压对人体的伤害作用Table 1 Damage effect of shock wave overpressure on human body

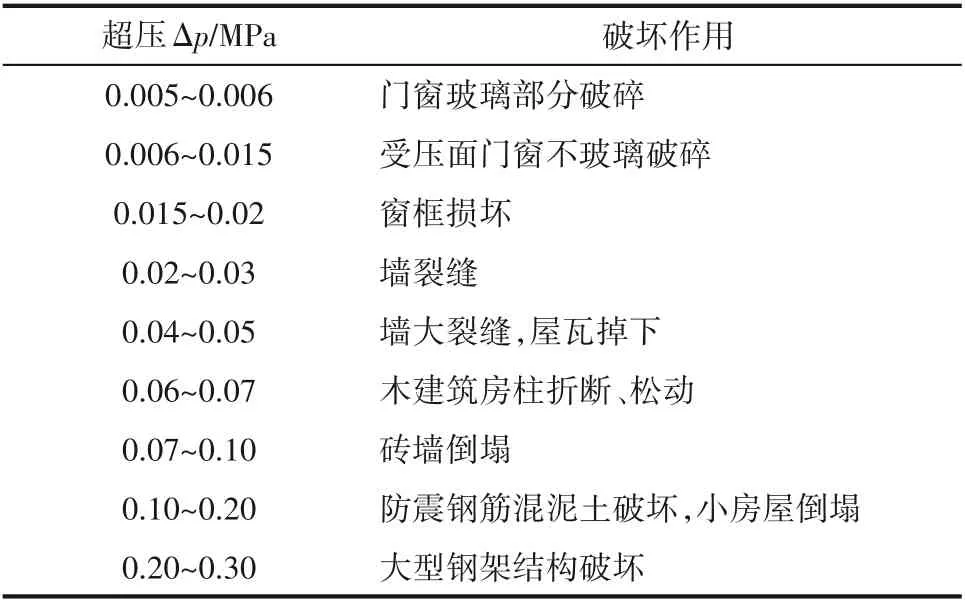
表2 冲击波超压对建筑物的破坏作用Table 2 Damage effect of shock wave overpressure on buildings

1.2 方程及模型选择

模型所利用到的基本空置方程有组分守恒方程、连续性方程、动量守恒方程以及能量守恒方程；经过对不同湍流模型，最终发现使用SAS 湍流模型得出的结果更符合实际，SAS 模型能够自动调整解析更小尺度的涡；燃烧模型分别用到了层流有限速率模型和涡-耗散-概念(EDC)模型。无约束爆炸过程中，气流的运动不受阻碍，其湍流程度较低，层流有限速率燃烧模型既可以满足计算精度又可以节约计算资源，但这一模型无法描述约束爆炸状况。涡-耗散-概念(EDC)模型在湍流的流动结构中纳入详细的化学反应机理。它假设化学反应均发生在小涡当中，称为精细涡。反应时间由小涡生存时间和化学反应本身所需要的时间来共同控制。其可以更好地描述湍流程度较高地燃烧过程。

在Fluent 中，假设小涡中的化学反应发生在相同条件下，初始条件取为单元中当前的组分和温度。组分守恒方程中的化学反应源项由式(1)得出。

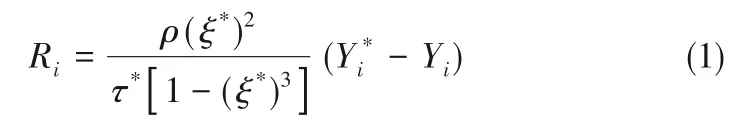
式中，Ri为化学反应源项；ε*为小涡的尺度；ρ 为密度，kg/m3;Y*为经过一段时间的反应后，小尺度组分的质量分数；τ*为反应经过的时间尺度；Y 为同样的物质在反应之前的浓度;上角标*表示小尺度；下角标i表示第i种物质。

2 仿真模型建立与实验验证

首先建立无约束超压冲击波传播模型，并使用实验数据进行修正，得到一种可行的超压传播仿真模型，然后通过分析有无约束对爆炸超压冲击波传播过程的影响，对无约束爆炸模型进行修正并应用于约束条件下的爆炸过程，分析障碍物周围及障碍物内部在预混气体爆炸时压力场的分布。

2.1 无约束爆炸仿真计算

2.1.1 无约束爆炸仿真模型建立 足够的网格密度是保证Fluent 计算精度的关键，但是受计算机计算能力和所需计算时间的限制，无法对网格进行无限加密。因此需要对不同网格密度进行计算分析，找到合理的网格密度，以确保计算效率[27]。本研究共设置三个不同网格密度，分别编为1#、2#、3#，具体的网格信息如表3所示，三种网格的质量均在0.6以上，能够较好的满足Fluent的计算要求。

对边长为2 m 的近地面甲烷/空气预混爆炸进行数值模拟，使用中心点火方式，检测距点火点水平位置为2 m处的超压，得到的结果如图1所示。

表3 网格信息Table3 Grid information

图1 网格敏感性分析结果Fig.1 Sensitivity analysis of grid

由图1 可见，2#与3#的计算结果，对于正超压峰值和负超压峰值相对误差均小于5%，因此2#的网格密度比较适宜，能够在保证计算结果可靠性的基础上节约计算资源和计算时间，故本次研究采用2#的网格密度。

使用甲烷单步反应方程式，其具体形式如下：

该化学模型的指前因子取值为1.35×1020，活化能为1.225×108J/kmol[28]。

建立一边长为2 m 的甲烷/空气预混立方体爆炸模型，预混气体浓度为化学计量浓度9.5%(体积)，中心点火。计算监测点为地面上距爆心水平距离为2 m 的位置。考虑到无约束爆炸的对称性以及节约计算资源，首先建立无约束爆炸二维仿真模型，并对中心点火区域另行加密，网格如图2所示。

图2 无约束爆炸模型网格示意图Fig.2 Schematic diagram of unconstrained explosion model grid

考虑计算精度及计算机资源占用，时间步长取1×10-5s。在无约束爆炸中，由于没有障碍物引起火焰锋面的褶皱，故而燃烧反应的湍流程度较低，因此层流燃烧模型更适合无约束爆炸工况[29-30]。边界条件使用符合实际的压力出口，采用PISO 算法，二阶迎风格式。

为选择适合的湍流模型，分别对k-ε湍流模型、k-ε 湍流模型以及SAS 湍流模型进行模拟分析，使用不同湍流模型进行计算。表4总结了不同湍流模型的峰值超压及峰值超压到达时间。对比后续2.2节中实验数据，可知SAS 湍流模型的计算结果更为接近实验数据，因此选择SAS 湍流模型来进行后续数值模拟。

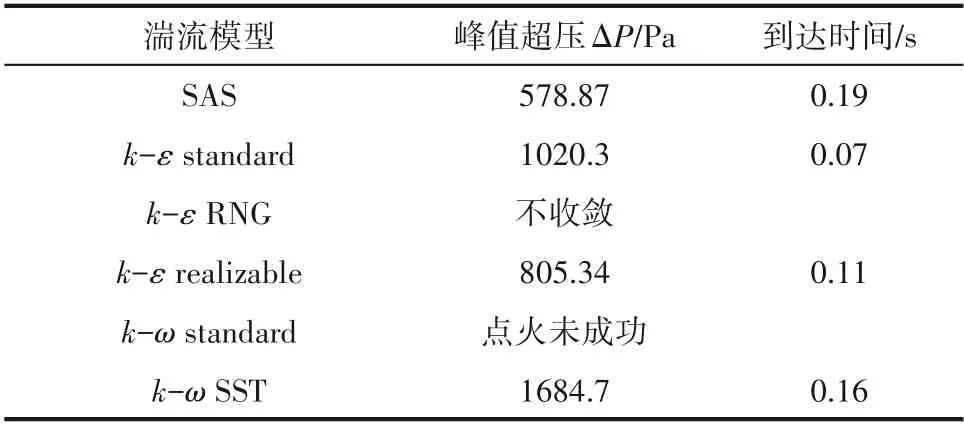
表4 不同湍流模型峰值超压与到达时间对比Table 4 Comparison of peak overpressure and arrival time of different turbulence models

采用Patch(定义某一局部条件)高温区的方式进行点火，模型点火温度选择为能够点着的最低温度1500 K，使用式(2)计算以1500 K 高温点火的点火能量，当点火区域半径为0.004 m 时，点火能量为100 mJ。

式中，Q 是点火能量，mJ；c 是比热容，kJ/(kg·mol)；m是被点火区域气体质量，kg；T是温度，℃。

保持点火温度1500 K 不变，改变点火体积来改变点火能量，数值计算研究了球体点火区域半径分别为0.004、0.006、0.008 和0.01 m 时点火能量对爆炸超压的影响，结果列于表5中。由结果可知，在弱点火能情况下，点火能量的少许改变对爆炸超压的影响并不大，因此后续模拟采用0.004 m 的点火球体半径。

表5 点火能量对爆炸超压的影响Table 5 Effect of ignition energy on explosion overpressure

2.1.2 无约束爆炸峰值超压模拟计算 针对无约束条件下，不同体积的化学计量浓度下甲烷/空气预混气云，采用上述方法进行模拟。共设置3 个不同体积的立方形预混气体爆炸工况，具体参数如表6所示。在爆炸中心线上，距爆炸中心点1、2、2.5、3和4 m处设置五个压力监测点。

表6 不同体积立方形预混气体爆炸工况条件Table 6 Explosion conditions of different volume cubic premixed gases

2.2 无约束爆炸峰值超压实验验证

由于开展甲烷气体爆炸实验成本高，难度大，因此本文使用Bao 等[12]的实验数据进行验证。Bao等[12]建立体积为V=1,8,27 m3的立方体形甲烷/空气预混气体进行了中心点火的无约束爆炸实验，预混气体满足甲烷燃烧的化学计量浓度[甲烷浓度c=9.5%(体积)]，点火能量为100 mJ。实验使用聚乙烯薄膜对预混气体进行固定，甲烷的预混及稳定均在薄膜内进行。实验验证聚乙烯薄膜会在超压产生瞬间破裂，对爆炸超压的影响微乎其微，可以忽略不计。压力监测点设置在地面上与点火点水平距离分别为d=2,2.5,3 m 的位置。具体的实验装置如图3 所示。图4 为距离点火点水平距离分别为d=2,2.5,3 m 的地面处的超压随时间的变化。

选取模拟过程中，预混气体边长为2 m 的工况与实验数据进行对比，模拟工况及监测点位置与实验相同，其模型示意图如图5 所示，图6 绘制了预混气体边长为2 m 的工况在三个监测点处的超压随时间变化图。

将图6 与图4 中对应实验数据进行比较可见，Fluent 数值计算结果一直处于波动状态，但总体趋势与实验结果相同。对于爆炸正负峰值超压的到达时间，Fluent 模拟结果要略小于实验数据，但在实际生产中，零点几秒的时间可以忽略，不会产生影响。对于峰值数值差异较大的现象，提出如下假设：数值模拟中预混气云内所有的甲烷均发生了完全燃烧，而实际实验工况中并非所有可燃物均能够发生完全燃烧，部分可燃物发生不完全燃烧反应，反应放出的热量小于模拟计算值；同时由于爆炸风的吹散，使得压力波附近的可燃气云被压缩，甲烷浓度升高，而外围还未反应的气云向周围扩撒，部分气云与空气再次发生混合稀释，甲烷浓度不再是化学计量浓度，甚至超出爆炸极限范围，故而实际爆炸工况产生的超压强度要低于数值模拟结果。下面将证明此种假设的正确性。

图7 绘制了预混气云边长2 m 工况中0.15、0.2和0.22 s时对应的甲烷体积浓度云图。

图3 实验装置图Fig.3 Diagram of experimental equipment

图4 无约束甲烷/空气预混爆炸在不同混合物体积、不同检测距离的实验数据结果Fig.4 Experimental results for unconstrained methane/air premixed explosions in different mixture volumes and different detection distances

图5 无约束爆炸模型示意图Fig.5 Schematic diagram of unconstrained explosion

由图7 可见，甲烷的反应一直在预混范围内进行，未曾发生气云的吹散。研究同时监测了距离爆心水平距离为1.1、1.3、1.5 m 处三点的甲烷浓度，在反应过程中其甲烷浓度一直保持为零。以上分析印证了Fluent计算模拟值较大原因的两条假设。

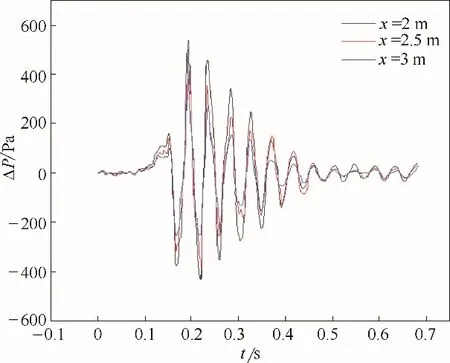
图6 边长2 m无约束预混立方气体爆炸Fluent数值模拟结果Fig.6 Fluent numerical simulation results of 2 m unconstrained premixed cubic gas explosion

为了直观地分析Fluent模拟计算值与实验值关系，表7列出了原始模拟计算值、实验值以及两者的比值关系。正负峰值超压的Fluent计算值与实验值的比值均在2.3～3.5之间，大部分比值都接近3，所以这里选择比值关系3 作为修正系数，即将Fluent 的原始模拟计算值乘以系数1/3 作为修正结果进行后续分析，且称修正后体积为当量体积。

图7 2 m工况对应甲烷体积浓度分布图Fig.7 Methane volume concentration distribution of case 2 m

表7 Fluent模型正负超压原始模拟计算值与实验值对比Table 7 The positive and negative overpressure original Fluent simulation results and experimental data

2.3 约束爆炸仿真模型建立

无约束条件下发生的预混爆炸，由于没有障碍物引起火焰锋面的褶皱，故而燃烧反应的湍流程度较低，而当气体爆炸影响区域内存在障碍物时，由于在传播过程中气体受到阻塞，火焰在通过障碍物时其锋面扭曲褶皱形成湍流旋涡，层流燃烧模型将不再适用。涡流耗散模型(EDC)能够在湍流反应流动中考虑详细的化学反应机理，计算精度高，可以用于描述由于障碍物存在产生的湍流旋涡。除此之外，障碍物存在不会改变预混爆炸的其他过程，因此，在无约束工况甲烷预混爆炸数值模型的基础上，将层流燃烧模型换为EDC 模型，即可用来完成甲烷预混气体约束爆炸模拟分析。

在上述研究的基础上，使用选定的计算方法，建立约束条件下甲烷/空气预混爆炸的三维仿真模型：立方预混气体体积8 m3，处于化学计量浓度，距地面高度1 m；监测区域为20 m×20 m×15 m 的长方体区域；障碍物长宽高为1 m×2 m×4 m，距爆心2 m，如图8 所示。监测点设置在障碍物的三个位置处：与爆心高度相同的正对爆炸面及背面，位于地面上的正对爆炸面及背面，以及顶部中心线处，具体分布如图9 所示。网格尺寸与无约束工况相同，选为空气区域0.2 m×0.2 m×0.2 m，可燃物区域0.02 m×0.02 m×0.02 m，点火区域加密0.005 m×0.005 m×0.005 m，在障碍物壁面附近同样进行了网格加密，其他设置不变，建立用于计算约束爆炸的仿真模型。

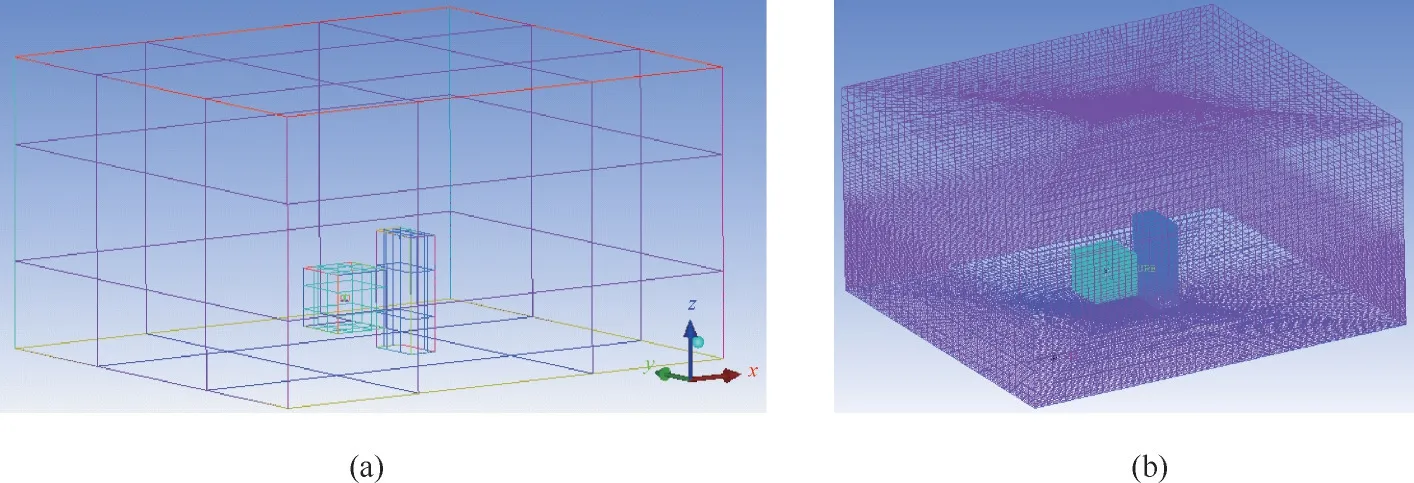
图8 障碍物的布置(a)与网格划分(b)Fig.8 Schematic diagram of obstacle arrangement(a)and meshing(b)

图9 监测点布置示意图Fig.9 Schematic diagram of monitoring point

3 障碍物存在工况下甲烷预混爆炸数值分析

主要从障碍物的高度、宽度两个方面考虑，以数值模拟的方法来研究气云爆炸在障碍物周围压力场的分布，并进一步探究了障碍物内部的压力场。

3.1 数值模拟工况设置

按照上述模型建立方法，通过改变障碍物几何特征，得到表8 所示几种仿真工况，分别研究了障碍物的高度和宽度对障碍物周围压力场分布的影响。

3.2 障碍物高度的影响结果分析

共设置5 个研究工况A-1～A-5，研究障碍物高度对爆炸后果的影响。障碍物的宽度均为2 m，厚度为1 m，障碍物正面到爆心的水平距离为2 m，障碍物的高度h 从2 m 增加到6 m，应用2.3 节建立的模型进行计算，并对结果进行1/3 修正。因A-3、B-2 条件设置相同，选A-3 作为参比工况。图10 展示了A-3(h=4 m)工况不同时刻通过爆心的XZ 平面压力场分布图。

由图10 可见，当预混气云附近存在障碍物时，压力场的分布不再是对称的。正超压场明显偏向于障碍物侧，负超压场则偏向于无障碍物侧，持续时间更长，但障碍物侧的负超压绝对值更大。障碍物的存在对正超压的传播起到了一定的阻挡作用，障碍物后的正超压值相对较低，但后部会受到负压的强烈冲击，这在无障碍物侧距离相等的位置是不存在的。爆炸产生的压力场一直处在正负超压的振荡之中，短时间内并不会回到零超压。

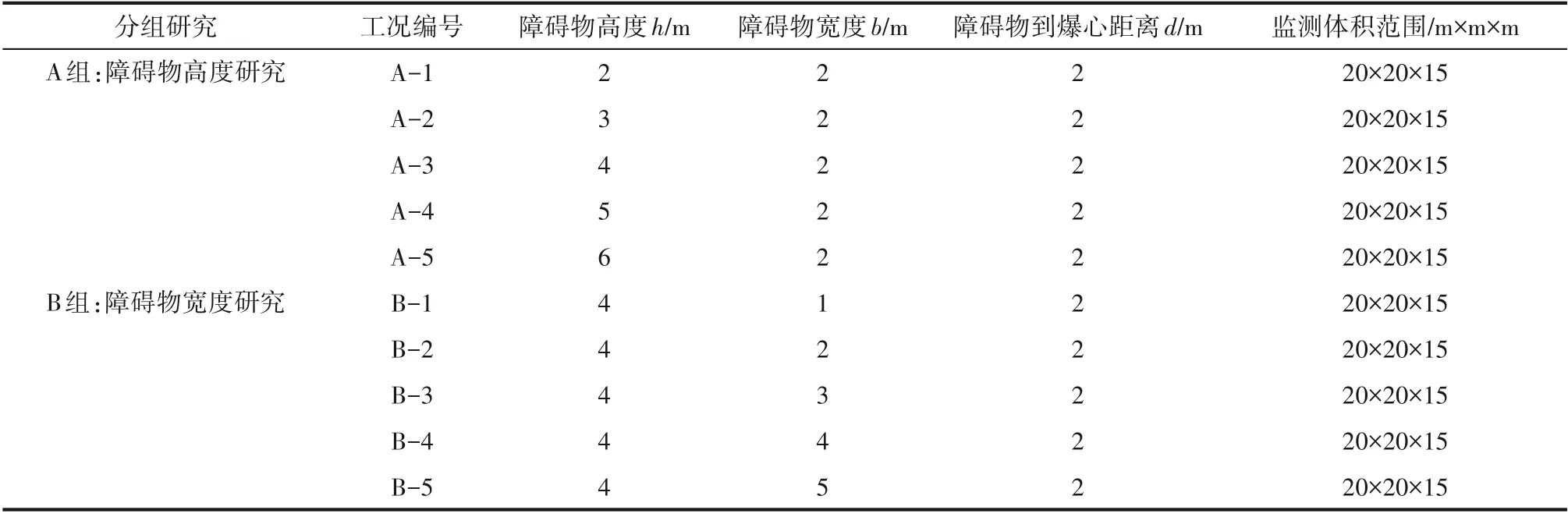
表8 障碍物研究工况条件设置表Table 8 Obstacle research conditions setting table

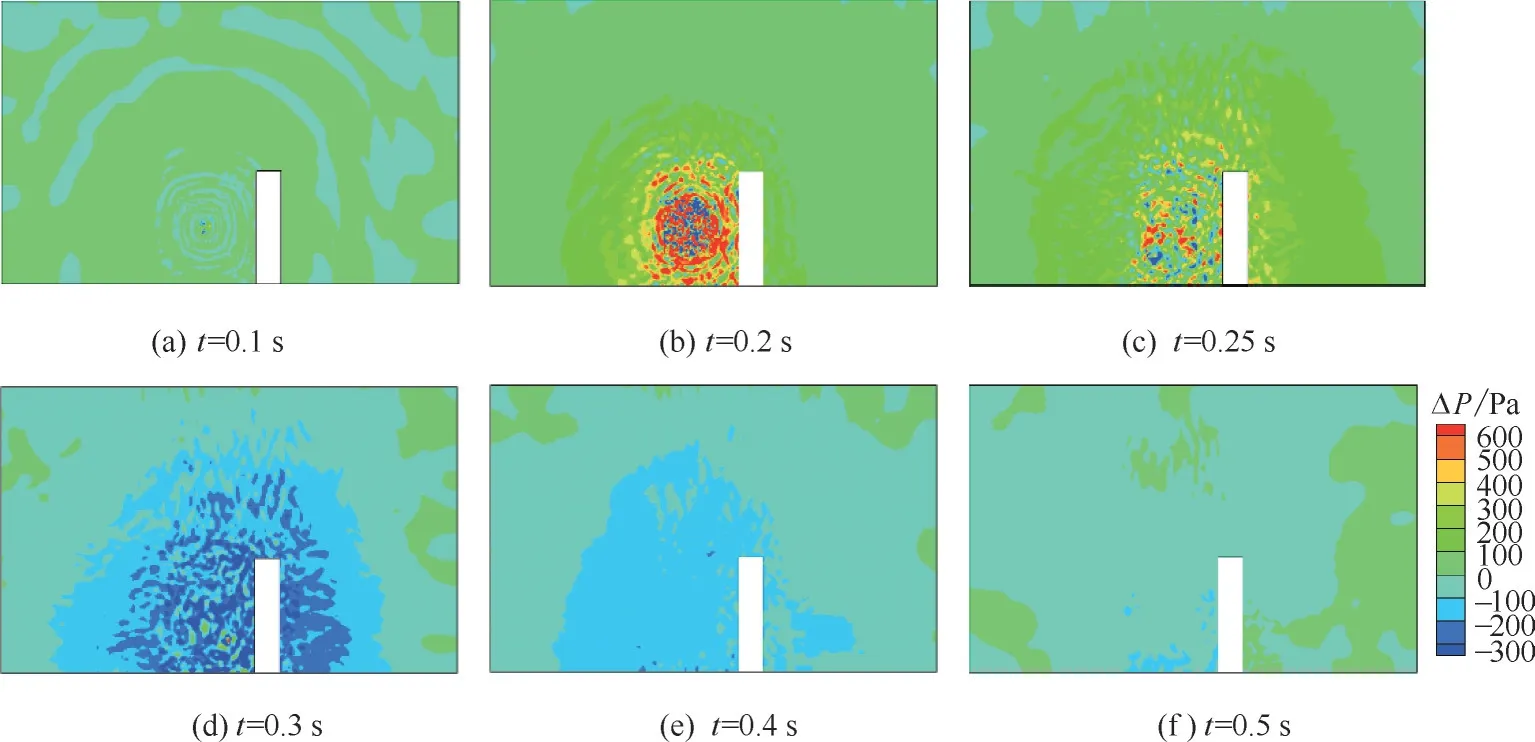
图10 A-3工况不同时刻通过爆心的XZ平面压力场分布图Fig.10 Pressure distribution of XZ plane passing through the ignition point at different times for case A-3

对于A 组障碍物工况，分别在障碍物正对爆炸面和背面的半侧宽度设置监测点，高度两米处(与爆炸中心高度相同)4 个和地面处4 个。图11 绘制了障碍物正对爆炸面上的超压分布，实线为与爆炸中心同高度处的超压分布，虚线为地面处的超压分布。

由图11 可知，从障碍物的中轴线向两侧方向正负超压绝对值有所下降。对比实线簇与虚线簇，总体上地面处的超压要大于与爆心水平高度处，这是由于地面与障碍物围成的夹角阻碍了气体的传波，极大地增强了气体的湍流强度，压力波在拐角处的多次折射也增大了总体的压力强度，造成地面处的超压升高。这表明，在实际遇到爆炸事故时，不要盲目地从建筑物上层向下层疏散，障碍物下层受到正负超压的反复冲击，极易对人体造成损害[31]。

如图12 所示，在障碍物背对爆炸源的一面，随着障碍物高度的增加，障碍物后侧的正峰值超压减小，但负峰值超压不断增大。这说明障碍物的背面有一定的抵御爆炸正超压的能力。同时，当障碍物高度升高到一定值，也即高宽比较大时(h=6 m 工况)，障碍物造成的湍流对超压的增强作于强于其抵御作用，障碍物后侧超压将会急剧增大。对比前后两侧的压差可以得到同样的特性，随着障碍物高度的增加，两侧压差逐渐增大，但当障碍物高宽比较大时，压差又出现减小的趋势。这是由于正对爆炸面在地面与障碍物形成的拐角处由湍流增大的超压更加容易绕过障碍物传播至其后侧空间。与障碍物正面的超压场相同，背面同样呈现地面处的正负超压绝对值均大于爆心水平面的超压值。综合来看，障碍物背对爆炸面的中上部才是最安全的位置，在实际爆炸工况中不应盲目向建筑物下部撤离。

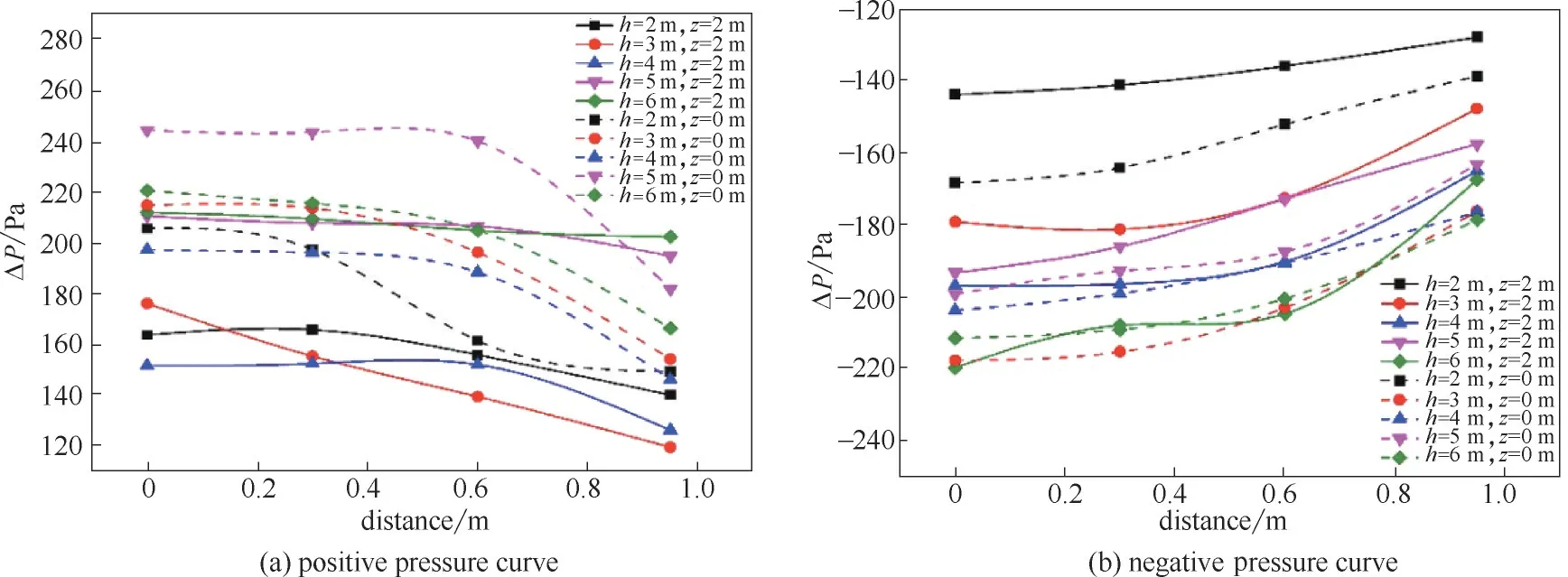
图11 A组障碍物正对爆炸面超压分布曲线Fig.11 Overpressure distribution on the facing surface of obstacles of case group A

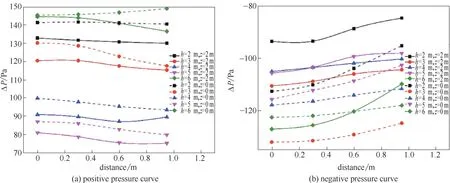
图12 A组障碍物背对爆炸面超压分布曲线Fig.12 Overpressure distribution on the back surface of obstacles of case group A

3.3 障碍物宽度的影响结果分析

设置5 个研究工况编号B-1～B-5，研究障碍物宽度对爆炸后果的影响。障碍物的高度均为4 m，厚度为1 m，障碍物正面到爆心的水平距离为2 m，障碍物的宽度b 从1 m 增加到5 m，使用与3.2 节相同的计算方法。为了更加直观地分析障碍物宽度对爆炸超压的影响，将各个工况最大正负超压对应时刻过爆心的XZ 平面压力场绘制于图13 和图14中。

由图可知，随着障碍物宽度的增加，爆炸的影响范围不断增大。当障碍物宽度增大时，地面与障碍物的拐角处气体聚集并发生湍流增强作用，正超压在拐角处急剧增大。障碍物对爆炸正超压具有较好的抵御作用。负超压的绝对值在障碍物宽度增加后同样逐步升高，负压场出现不对称性，障碍物一侧的负压范围增大。并且障碍物宽度增大后，障碍物后侧出现大范围的高强负压场，说明障碍物对负压的抵御能力较弱。

对B 组障碍物宽度工况，分别在障碍物正对爆炸面和背面的半侧宽度上设置监测点，监测点高度分别设在2 m 高度处(与爆炸中心高度相同)和地面处。工况B-1、B-2 同一高度设置4 个监测点，工况B-3、B-4、B-5 在同一高度设置5 个监测点。图15绘制了障碍物正对爆炸源面的超压分布，实线为与爆炸中心同高度处的超压分布，虚线为地面处的超压分布。

图13 B组工况爆炸最大正超压对应时刻压力场Fig.13 Pressure fields at maximum positive overpressure corresponding time for case group B

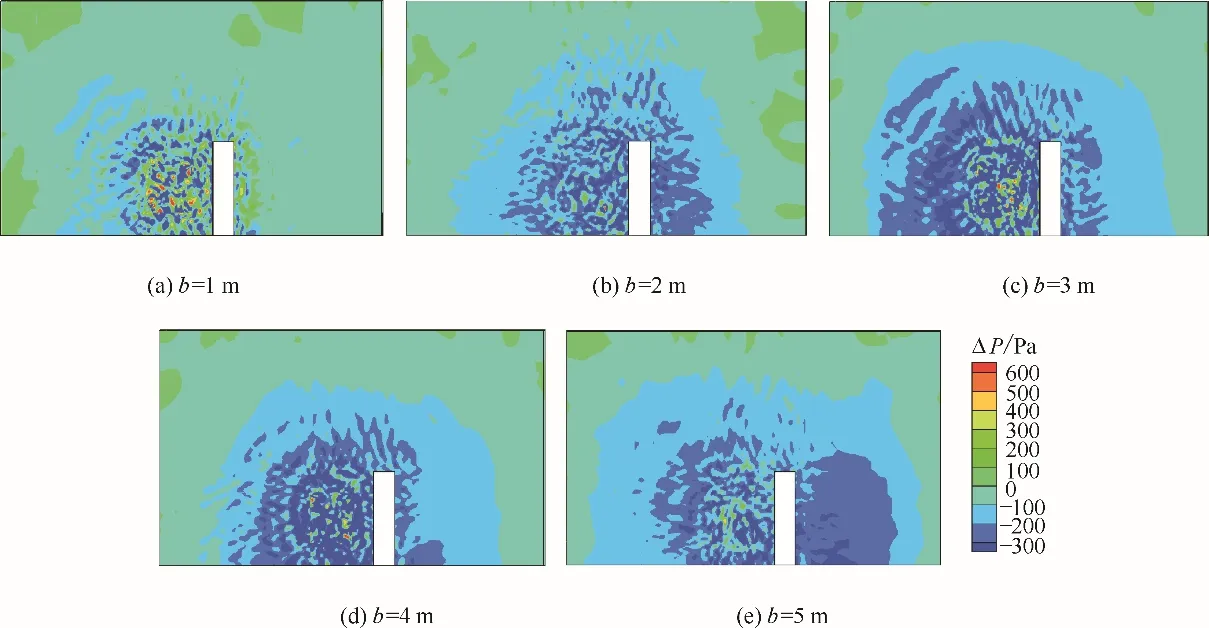
图14 B组工况爆炸最大负超压对应时刻压力场Fig.14 Pressure fields at maximum negative overpressure corresponding time for case group B

图15 B组障碍物正对爆炸面超压分布曲线Fig.15 Overpressure distribution on the facing surface of obstacles of case group B

对比实线簇与虚线簇，总体上在障碍物正对爆炸的一侧，地面附近无论正负超压，其绝对值总是要大于上方与爆心同高度的位置，与高度工况相同，说明在地面与障碍物形成的拐角处可燃气发生积聚，在增加湍流程度的同时增大了爆炸超压。对于负压，随着障碍物宽度的增加，负超压的绝对值呈现先上升后下降的趋势，同时上下不同位置的压差逐渐减小，说明随着障碍物宽度的增大，对负压具有削弱作用。在障碍物宽度方向上，正负超压绝对值呈现出由中轴线向两侧递减的趋势。

如图16 所示，在障碍物背对爆炸源的一面，随着障碍物宽度的增加，障碍物后侧的正峰值超压不断减小，但负峰值超压总体上呈现小范围的波动。

对比同一工况障碍物前后两面的正超压值可以发现压差不断增大，这说明障碍物宽度的增加，使得其抵御爆炸正超压的能力不断提高，能够有效减轻正超压对障碍物后方的破坏。但对于负超压来说，两侧压差并没有明显的变化，障碍物宽度的增加对其抵御负超压的能力并无显著效果，障碍物后方主要承受负压破坏。与障碍物正面的超压场相同，背面同样呈现地面处的正负超压绝对值均大于爆心水平面的超压值，负压强度要高于正压。综合来看，障碍物宽度是其抵御爆炸正超压能力的重要因素。

3.4 障碍物内部压力场分布

图16 B组障碍物背对爆炸源面超压分布曲线Fig.16 Overpressure distribution on the back surface of obstacles of case group B

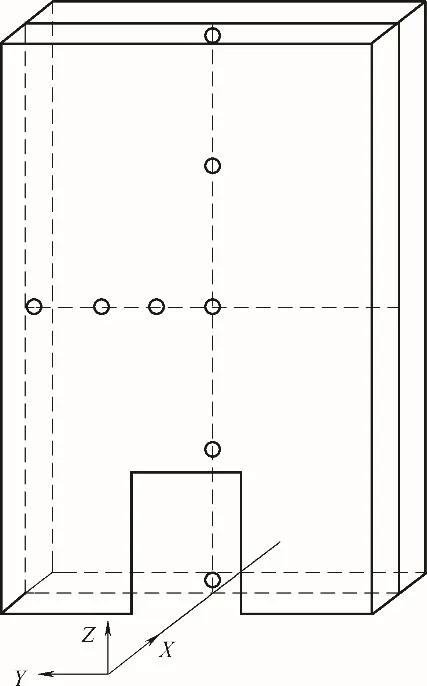
图17 障碍物内部监测点布置Fig.17 The monitor points arrangement in obstacle

3.2节、3.3节中均假设障碍物是全封闭的，能够对内部起到有效的保护，但实际工况中的建筑物并非完全封闭。为了研究障碍物内部的压力场，设立工况C，障碍物尺寸与标准工况中相同(宽2 m，厚1 m，高4 m)，距离爆炸中心的距离为2 m，壳体厚度0.05 m。在障碍物下部开口0.6 m×1 m，模拟建筑物大门。障碍物内部监测点设置在中心YZ平面上，具体布置如图17所示。

经过Fluent 数值模拟计算，将封闭障碍物工况(A-3)和开门障碍物工况C 在爆炸过程中的最大正负超压值列于表9中。当障碍物存在一个下部开口时，对整个爆炸的最大正超压影响并不大，但会明显降低爆炸负超压的最大绝对值。

在研究障碍物内部压力场之前，首先对障碍物下部开口后对其外部超压场的影响进行分析。图18 绘制了两个工况障碍物正对爆炸面半侧宽度上由中心向一侧超压的变化，其中实线代表z=2 m 高度上(与爆心同高)的超压，虚线代表地面上(z=0 m)的超压。

表9 工况A-3与工况C最大正负超压对比Table 9 Maximum overpressure comparison between case A-3 and case C

由图可见，当障碍物下部开门后，爆心水平面上的正超压略有降低，但并不明显。地面处的正超压相较于封闭式障碍物大大降低，这是因为原来积聚在此处的气体能够向障碍物内部流动，大大降低了阻塞率。障碍物下部开口后，正侧的负超压变化并不明显。

图19 为两个工况障碍物背对爆炸面半侧宽度上由中心向一侧超压的变化，同样实线代表z=2 m高度上(与爆心同高)的超压，虚线代表地面上(z=0 m)的超压。障碍物下部开门后，对于爆心水平面上的正负超压均无明显变化，但对于地面处，障碍物后侧的正负超压绝对值均显著增大。

在此基础上，对障碍物内部的压力场进行分析，图20 为与爆炸中心同高度2 m 处，障碍物内部半侧宽度上由中轴线向一侧的超压变化，图21则为障碍物中轴线上，由地面向上正负超压的变化。

由障碍物中心至两侧正负超压有少许下降，但并不明显，总体上正负超压的绝对值大致与障碍物背面相同，说明障碍物对内部有较好的保护作用。随着高度的增加，正负超压的绝对值均明显下降，正超压的下降速度大于负超压。

图18 工况A-3和工况C障碍物正对爆炸侧正负超压分布Fig.18 Overpressure distribution on the facing surface of obstacles for case A-3 and case C

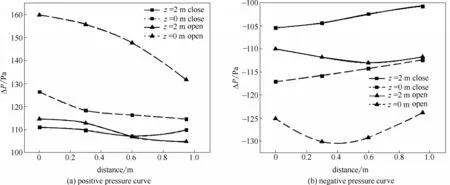
图19 工况A-3和工况C障碍物背对爆炸侧正负超压分布Fig.19 Overpressure distribution on the back surface of obstacles for case A-3 and case C

图20 障碍物内部z=2 m半侧宽度上正负超压的变化Fig.20 Overpressure change diagram inside the obstacle on z=2 m height

总体来看，在建筑物不失效的前提下，即建筑物不坍塌能够对内部进行有效保护的情况下，越靠近障碍物的上层与两侧越安全。在紧急爆炸事故中，盲目的向下逃生，反而容易受到正负超压的强烈冲击。

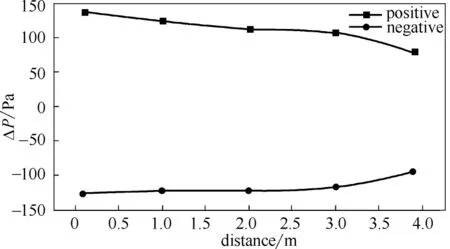
图21 障碍物内部中轴线上正负超压随高度的变化Fig.21 Overpressure changes with height on the inner axis of the obstacle

4 结 论

文章针对天然气泄漏甲烷预混爆炸的无约束工况，建立了峰值超压模型，并利用实验加以修正，分析对比有无障碍物时气体预混爆炸的区别，将所建立模型修正后应用于障碍物存在时的爆炸情形，分析了气体爆炸时障碍物周围及内部的压力场分布，主要得到以下结论。

(1)经过对Fluent不同模型的分析以及与实验数据的对比，SAS湍流模型、层流燃烧模型最为适合甲烷无约束预混爆炸，由于湍流程度不同，EDC 燃烧模型更为适用于约束爆炸情形。

(2)在弱点火能情况下，点火能量的少许改变对爆炸超压的影响并不大。处于爆炸外围的气体会在冲击波的作用下进一步与空气发生混合，其浓度可以降低到爆炸下限之外，而压力波附近的可燃气云被压缩，甲烷浓度升高，这部分甲烷将不完全燃烧甚至不燃烧。按照文章给出的仿真模型计算，模拟值与实验值峰值之比近似为3。

(3)障碍物的存在对正超压的传播起到了一定的阻挡作用，障碍物后的正超压值相对较低，但会受到负压的强烈冲击。随着障碍物宽度的增加，其抵御正超压的能力不断提高。在障碍物竖直方向上，贴近地面处受地面与障碍物围成的夹角的影响，湍流强度及超压峰值会极大增强。

(4)综合来看，背对爆炸面的中上部是最安全的位置，实际发生爆炸时，不要盲目自上而下撤离。在建筑物不失效的前提下，建筑物内部越靠近障碍物的上层与两侧超压值越小，更为安全。

符 号 说 明

c——比热容，kJ/(kg·mol)

m——被点火区域气体质量，kg

Q——点火能量，mJ

T——温度，℃

ρ——密度，kg/m3

下角标

i——参与反应的第i种物质，i=1,2,3,…