颗粒黏度模型对采用欧拉多相流模型模拟超密相颗粒流动行为的影响
2020-11-18姚晶星杨遥黄正梁孙婧元王靖岱1阳永荣1
姚晶星,杨遥,黄正梁,孙婧元,王靖岱1,,阳永荣1,
(1 浙江大学化学工程联合国家重点实验室,浙江杭州310027; 2 浙江省化工高效制造技术重点实验室,浙江杭州310027; 3 浙江大学化学工程与生物工程学院,浙江杭州310027)
引 言
在实际生产过程中,许多工艺设备不可避免地存在密相颗粒流动,例如流化床、循环流化床、料仓、气固密相移动床等,研究颗粒的流动行为对这些设备的设计和操作十分重要。一方面,反应设备中颗粒的流动行为会直接影响传质传热效率进而影响反应转化率;另一方面,当颗粒以整体流流动时,会在壁面处造成应力扰动,对设备的安全运行造成威胁[1]。研究设备内部颗粒流动行为的方法包括实验和模拟两种。实验方法主要依赖一定的检测手段,诸如示踪颗粒法[2-3]、电导探针法[4]、PIV 技术[5-6]、断层扫描[7-9]等。然而,这些方法大多因某些缺点难以应用到实际生产过程中,如侵入式检测会破坏原本颗粒流场;成像法易受重叠颗粒干扰,难以准确反映床层内部的流动信息。近年来,计算流体力学(CFD)的快速发展使得分析三维空间内复杂流动行为成为了可能,其相较于实验检测方法,有着安全性高、成本低、流场无干扰等优点。因此,CFD 被广泛应用于反应器设计、结构优化以及放大等领域[10-14]。
目前用于计算颗粒流动行为的建模方法主要分为两类:离散相方法和连续性方法。离散相方法的典型代表是离散单元法(DEM)。DEM 集中在颗粒尺度上,对单个颗粒进行受力分析,以获得颗粒的运动轨迹[15-17],具有极高的精确性,但也带来了繁重的计算量。针对大流域的体系,连续性方法的优点更加突出。其中,欧拉多相流模型的应用最为广泛,其采用拟流体方法将颗粒简化为流体,并引入了颗粒动理论(KTGF)建立拟流体状态下颗粒的本构方程,进而将各相处理成互相贯穿的连续介质,并对每一相建立动量方程和连续性方程。相较于DEM 方法,欧拉多相流模型既在一定范围内保障了模型精度又大幅减少了计算量。Gidaspow[18]首次提出欧拉多相流的模型,其忽略了与固体黏度有关的应力,成功预测了鼓泡床中空隙率和气速的变化,甚至能够预测气泡的形成及其后续演变。Lan 等[19]探究了固相壁面边界条件对欧拉双流体模型的影响,发现镜面反射系数对喷动床的喷射行为有着显著的影响,并给出了其体系的最佳值0.05,而颗粒-壁面恢复系数的影响则很小。Srivastava 等[20]对Schaeffer 摩擦应力模型进行了修正,建立了新型摩擦动力学流变模型,该模型成功描述了料仓重力卸料过程中出口的颗粒流动行为和流化床中的气泡上升时摩擦对气泡形状的影响。He 等[21]采用欧拉多相流方法模拟了三维矩形径向移动床中空腔的形成和发展过程。其模拟结果表明空腔尺寸会随着气速的增加而增大。Bertuola 等[22]通过连续性模型预测了料仓中二元颗粒混合物排放过程中偏析现象的发生和演变,并与独立的文献实验数据对比,一致性非常好,均方根误差小于10%。Tian 等[23]比较了三种常用摩擦黏度模型Schaeffer、S-S、μ(I)对颗粒流动的影响,并与DEM 的模拟结果进行对比评估,但是其建模对象局限于平底料仓,没有考虑气固相间作用力对颗粒流动的影响。而在大多数气固两相流体系中,气固相间作用力会改变颗粒运动状态,在两相耦合计算模型中有着重要的影响。Du等[24]在喷动床体系中考察了不同气固阻力模型,并与He等[25]的实验数据对比,其结果表明Gidaspow 模型的结果与实验最为接近。
上述研究结果均表明,采用欧拉多相流模型模拟密相固体流动具有一定的可行性。但是将固体颗粒作为拟流体相,不可避免地使其具有流体参数,例如剪切黏度,这一参数反映了颗粒间碰撞、摩擦等行为,在模拟密相颗粒流动时该参数对计算结果有显著影响。摩擦压力和径向分布函数是计算颗粒剪切黏度的两个重要参数,然而,当固体分数极高时,其计算模型会出现显著差异[26],对颗粒流动行为的预测造成影响。目前尚未有文献对高固含率下颗粒摩擦压力和径向分布函数模型的选取和CFD 模型参数的优化进行研究,这也使得欧拉多相流模型在高固含率条件下的应用存在一定的局限性。
因此,本文以气固并流向下的移动床为对象,以实验测得的压力和固体流率为基准,考察了采用欧拉多相流模型模拟高固含率下气固流动行为时摩擦压力模型(Johnson 模型、Based 模型)和径向分布函数模型(Lun 模型、Syamlal O’Brien 模型)对模型结果的影响,期望为这些模型的选取提供指导。同时,本文还探究了本体系下模型的最优参数设置。
1 实验装置与方法
实验装置如图1 所示,为气固并流向下的矩形移动床,高870 mm、长100 mm、宽40 mm。收缩段斜边与水平面夹角45°,出口管内径26 mm。固体(直径3 mm,陶瓷球)通过进料管直接进入床层,气体(空气)先通过顶部的气体分布板,分布均匀后再进入床层。
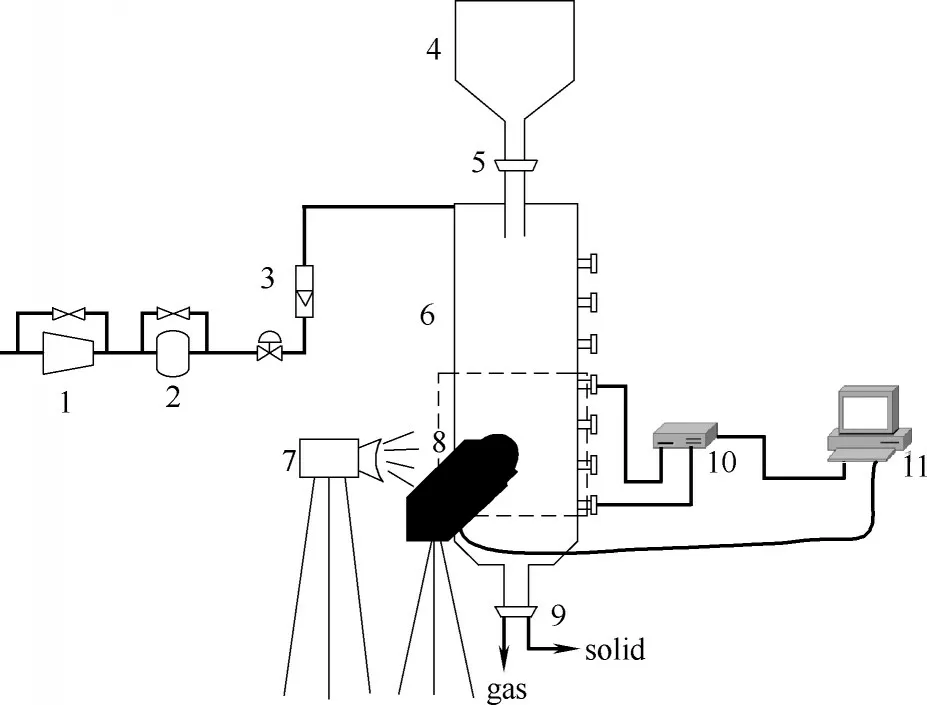
图1 气固移动床冷模实验装置Fig.1 Cold-model experimental system for gas-solid moving bed reactor
实验正式开始前,先打开颗粒进口阀门,使颗粒自由填充床层,随后打开风机,通入气体,打开出口阀门,气固相并流向下流动。待气固相流动稳定5min 后,通过差压传感器(1151DP 型传感器)测量床层壁面压降;通过电子天平(YP10K-1)测定出口固体质量流率;通过高速相机(Photron Fastcam MiniWX100, Japan)以及Photron 配套软件,在气体分布器下方500 mm 处的位置拍摄分辨率为2048×2048 像素的图像。实验中使用光源为LED 背光源,光强度为4000 cd,使用镜头为尼康相机自动对焦镜头(AF 50/1.8D),采集速度设置为每秒50 帧,曝光时间为1/20000 s,采集时间30 s,得到气固流动图像,并进一步通过MicroVec 软件处理得到壁面颗粒速度分布。
2 数学模型与模拟条件
2.1 模型方程
本工作采用欧拉多相流模型,将固体相简化为拟流体相,表1为气固两相主要的模型方程表达式[27-30],并在图2展示了固体各模型方程间的逻辑关系。
由图2 可知,摩擦压力和径向分布函数是计算颗粒剪切黏度的两个重要参数。但在高固含率条件下,不同模型方程所使用的摩擦压力和径向分布函数有着显著的差异[26]。
摩擦压力大多是半经验模型。Johnson 等[31]基于干燥的无黏聚性颗粒的实验数据对摩擦区域内的固体压力提出了一个简单的代数式模型方程,具体形式如下。

Based 模型是一个简化模型,其摩擦压力等于固体压力,其通过将径向分布函数与固体压力耦合起来,使得Based 模型在高固含率下同样能够呈现出压力的渐近行为。
径向分布函数g0,ss是修正颗粒间碰撞概率的模型。Lun 等[27]在Ogawa 等[32]的基础上对模型进行了拓展,将其应用于多个颗粒相。
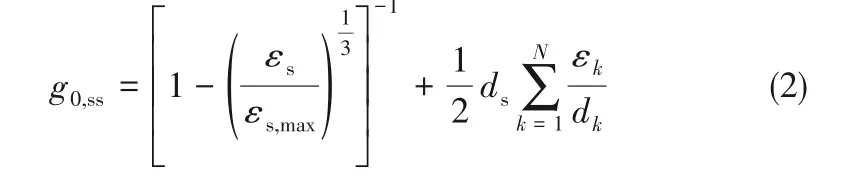
Lebowitz[33]推导出用于硬球模型的颗粒混合物模型——Syamlal O’Brien 模型(SO模型)。

从图3 中可看到Lun 模型与Syamlal O’Brien 模型的主要区别是当固体分数趋向于设置的体积上限时,Lun 模型计算g0,ss趋向于无穷,而Syamlal O’Brien 模型结果相对平稳。因此Syamlal O’Brien模型不能作为最大固含率的约束条件与Based 摩擦压力模型耦合使用。本工作将基于实验数据,评估Based-Lun 模型(BL 模型)、Johnson-Lun 模型(JL 模型)和Johnson-SO 模型(JSO 模型)三种模型组合的预测能力。

表1 数学模型方程Table 1 Mathematical formulas for simulation
2.2 模型参数设定
本工作以三维矩形气固移动床为研究对象,计算主体的几何尺寸为100 mm × 40 mm × 870 mm。反应器的结构主要分为进料段、锥形床层主体、虚拟计算域三个部分。气体采用速度入口边界,真实床层出口设为内部边界不添加额外约束条件。将计算域整体向下延伸100 mm,即CFD模型的实际边界不紧邻出口,而是在出口下方[20,23]。实验中由于颗粒料仓的存在,移动床稳定流动时,各相进出平衡,床层料位高度不变,利用UDF(用户自定义函数)使得颗粒进口流率等于出口流率来近似实现料仓的功能。干燥陶瓷球颗粒黏聚力很弱,内摩擦角≈休止角,通过休止角测量得到其内摩擦角近似值22°,通过称重法测得颗粒流动过程中床层固含率约为0.56。此外在模拟过程中,需要选择合适的计算时间,在保证计算结果准确性的同时减小计算量。根据实验测得的固体质量流率推算出颗粒从进口流到出口至少需要30 s 的流动时间。因此,先在气体流量1.0 m3·h-1、E1=150、E2=1.75的条件下,采用Johnson-Lun 模型组合计算至40 s,固体质量流率和床层单位高度压降的计算值随时间的变化如图4所示。由图4 可知,模型计算值在10 s 前便已经稳定。进一步,在气体流量1.0 m3·h-1、E1=457.12、E2=1.41条件下,采用Based-Lun模型组合计算至110 s,固体质量流率和床层单位高度压降随时间的变化如图5所示。由图5可知,模型计算值也在10 s前便已经稳定。因此模拟过程中设置颗粒内摩擦角θ=22°,初始填充固含率εs,initial= 0.56,壁面边界条件为无滑移壁面,计算流动时间10 s。气固移动床连续性模型其他参数设置见表2。
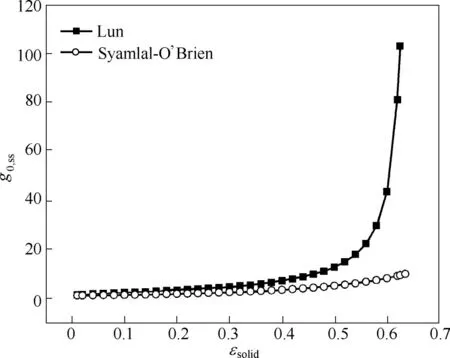
图3 单组分颗粒下不同径向分布函数随固含率的变化(εs,max=0.64)Fig.3 Radial distribution functions at different solid phase volume fraction
3 结果与分析
3.1 网格独立性检验
本文采用欧拉多相流模型对固体进行拟流体化处理,网格体积需大于颗粒,保证一个网格内有多个颗粒,满足固体简化成连续相的假设。为了探究本体系的最适宜网格尺寸,本工作采用了12、6、4 mm 三种不同网格尺寸划分网格,并进行网格独立性检验,结果如图6所示。由图可得,网格尺寸为6、4 mm 下的计算结果相差不大,流动稳定后,最大偏差仅为1.6%;而网格尺寸为12 mm时的床层单位高度压降大于其他条件下得到的床层单位高度压降。综上所述,本工作认为当网格尺寸≤6 mm 时,模拟结果与网格尺寸无关。因此本文采用6 mm 的网格尺寸划分计算域,并以此进行后续的模拟研究。
3.2 基础模型结果与对比
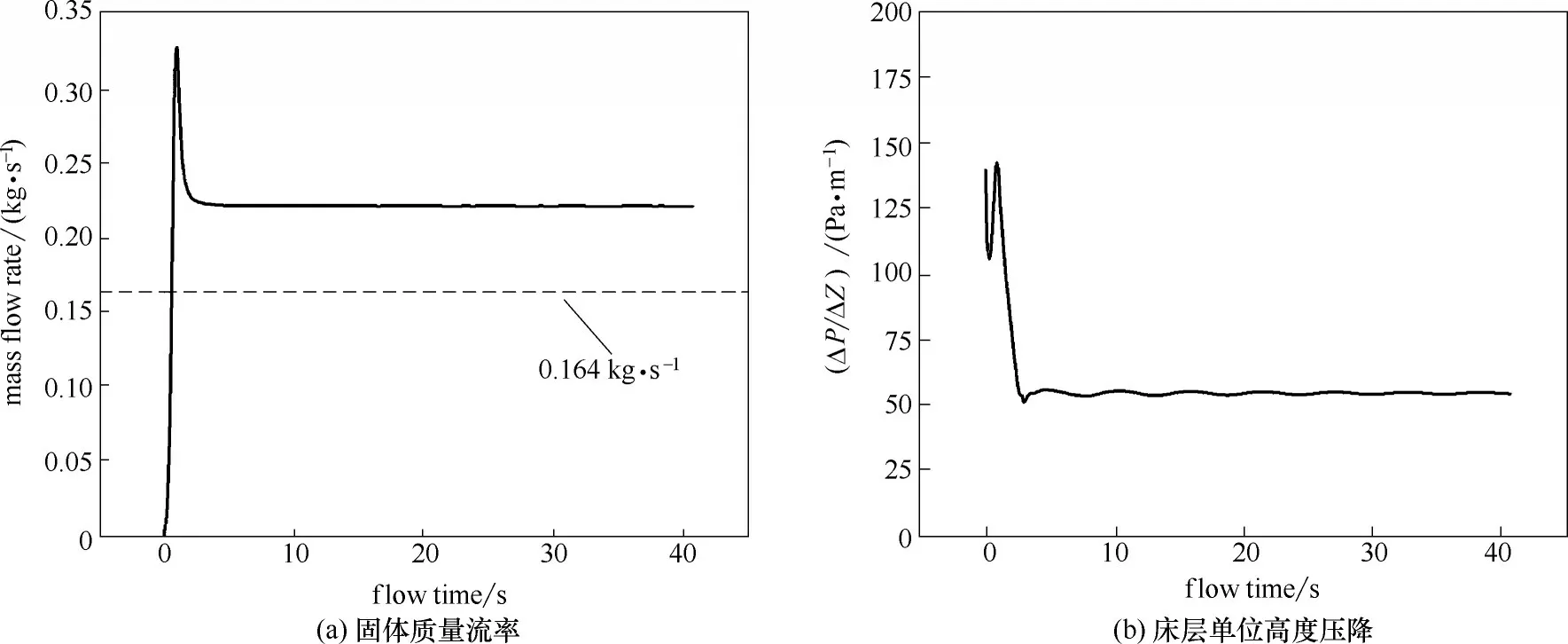
图4 Johnson-Lun模型组合预测结果随流动时间的变化Fig.4 Predicted results of Johnson-Lun model combination varied with flow time
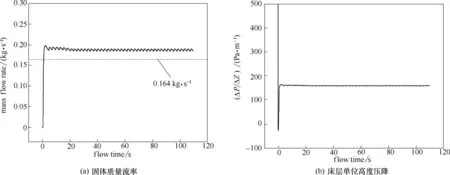
图5 Based-Lun模型组合预测结果随流动时间的变化Fig.5 Predicted results of Based-Lun model combination varied with flow time

表2 欧拉多相流模拟参数设置Table 2 Parameters setting of Euler multiphase flow simulations
图7 分别展示了不同模型组合Based-Lun、Johnson-Lun 和Johnson-SO 预测的固体出口质量流率、固体体积分数和压降结果。图7(a)表明同一径向分布函数Lun模型下,Based模型预测的固体质量流率小于Johnson 模型,而在摩擦压力模型同为Johnson 模型时,Syamlal O’Brien 模型预测的固体质量流率大于Lun模型。这表明摩擦压力模型与径向分布函数模型对固体质量流率有着显著的影响。本文的气固体系中,固体处于密相流动状态,此时颗粒间摩擦力在颗粒流动中占据主导地位。根据前文,固体碰撞概率与摩擦压力越大,固体黏度越大,固体流动性越差,流动速度越小。从图7 (b)可知Based 模型预测的固体体积分数与最大允许固含率十分接近,远大于Johnson 模型,因此Based 模型受到径向分布函数的约束,摩擦压力变大,黏度变大,遏制了固相流动。Syamlal O’Brien 模型预测的固体质量流率远大于Lun模型是由于当固体体积接近上限时,Syamlal O’Brien 模型计算的碰撞概率要明显小于Lun 模型,如图3 所示,因此其计算的黏度更小,固体质量流率更大。此外值得注意的是所有模型组合的质量流率预测值都高于实验值(0.164 kg·s-1)。这与Tian 等[23]的结论相一致,固体拟流体化的连续性欧拉模型对移动床固体出口速度的预测值偏高。Tian等认为这是由于Schaeffer摩擦黏度模型难以准确预测出口上方的固体体积分布,这也表明了固体体积分布对连续性模型的重要性。

图6 不同网格尺寸模拟结果Fig.6 Simulation results at different grid sizes
图7 (b) 给出了不同模型组合预测的固体体积分数在轴向上的分布信息。由图可得,随着床层高度的增加,Based-Lun 模型组合预测的固体体积分数减小,而Johnson-Lun 和Johnson-SO 模型组合预测的变化趋势则与之相反。此外Based-Lun 模型组合预测的固体体积分数明显高于Johnson-Lun 和Johnson-SO 模型组合。其固体体积分数轴向分布的标准差分别为7×10-4(BL 模型)、3.9×10-4(JL 模型)、4.6×10-4(JSO模型),表明Johnson模型计算的固体轴向分布比Based模型更加均匀。
图7 (c) 给出了不同模型组合预测的压力梯度以及实验测量值。由图可得,模型预测的压力梯度均明显低于实验值,且ΔPBL>ΔPJL>ΔPJSO。其原因主要有两点:首先是气固相对速度的差异,由图7(a)可知,三种模型组合预测的固体质量流率均大于实验测量值Qm,JSO>Qm,JL>Qm,BL,在进气量一定的情况下,不同模型组合预测的气速基本相同,因此固体速度越大,气固相对速度越小,气固相间曳力就小,压降就小;其次是欧根系数E1、E2,欧根系数能够体现床层结构的影响,Gidaspow 曳力模型采用的E1、E2分别为150 和1.75,其值不一定适用于本工作中的实验体系,为了使建立的模型更加贴合实验体系,需要对E1、E2进行校正。
3.3 模型参数优化
3.3.1 欧根系数 由前文可知,三种模型组合的压降和固体流量预测值与实验值偏差较大,为了提高模拟准确度,本工作通过实验测得不同气速下的单位床层压降,拟合得到适合本体系的欧根系数E1=457.12,E2=1.41。该欧根系数能够准确反映床层结构的影响,具有物理意义。从前文得知床层固含率εs>0.2,Gidaspow 曳力模型可简化为欧根方程,将欧根系数修正值与模型耦合,进一步考察三种模型组合对气固流动行为的预测能力。图8展示了采用新欧根系数后不同模型预测的床层压降结果。由图可知,经过欧根系数修正后,模型预测的压降明显增加,虽然与实验值相比仍然偏低,但准确度显著提高,Based-Lun、Johnson-Lun 和Johnson-SO 模型组合的相对误差分别由68.6%、73.3%和78.2%降低至13.2%、29.7%和42.3%。
图9 进一步展示了在欧根系数修正后,三种模型组合所得到的固体体积分布随时间的演变,由图可见,不同组合的结果具有明显的差异。首先由图9 (a) 、(b) 可知,Based 模型预测的固体体积分数更大,其平均固体体积分数约为0.567,Johnson 模型预测的平均固体体积分数仅为0.531,而实验测得的固体体积分数为0.55~0.56。与实验值相比,Johnson模型预测值明显偏小,而Based 模型与实验值较为接近。此外Based 模型在真实出口上方以及进料段形成的“空腔”区域也更加明显,并且“空腔”会进行周期性运动。其次由图9 (b)、(c) 可知,相比Lun 模型,Syamlal O’Brien 模型在固体分布上能够更快到达稳定状态,并且其出口上方的“空腔”区域更小。这可能是由于Syamlal O’Brien 模型预测的固体流率更大,从而使得床层流动更快到达稳定。另外值得注意的是Johnson模型在预测固体体积分布时,出现了床层膨胀的现象。该现象的产生是由于Johnson 模型计算得到的固含率比预先填充的固含率小,但由于固体边界的设置,床层内总固含率是恒定不变的,故出现床层膨胀的现象。

图7 不同模型组合预测的固体速度、体积和气体压降Fig.7 Gas pressure drop and solid vertical velocity,volume fraction simulated by different model combinations
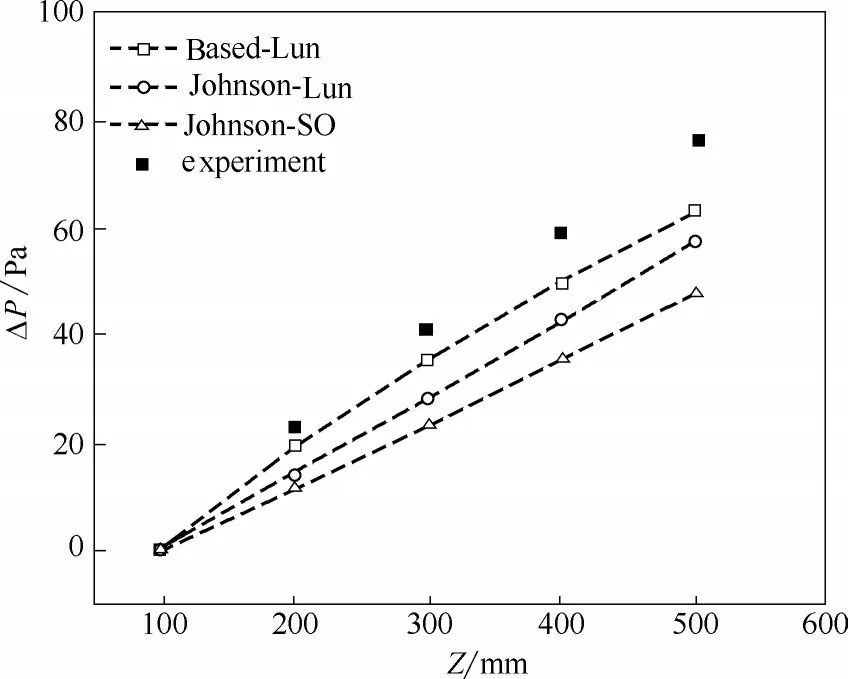
图8 修正欧根系数后不同模型组合预测的床层压降轴向分布Fig.8 Axial distribution of pressure drops simulated by different models after Ergun coefficients were modified
图10 给出了修正欧根系数后模型预测的近后壁面区域(距壁面1.5 mm)固体垂直速度与PIV测得的壁面颗粒速度的对比结果。由于壁面采用无滑移条件,导致左右两侧壁面附近的颗粒速度因壁面边界条件的影响迅速减小,与真实流动差距较大,因此图10 中仅给出了20~80 mm 范围内的对比结果。由图可知,PIV 测得壁面颗粒速度随径向位置变化不大,整体较为平稳,速度处在[-0.0208,-0.0191]区 间 内。而Based-Lun、Johnson-Lun 和Johnson-SO 模型组合计算的颗粒速度大小与高度有关,Based-Lun 模型组合预测的颗粒速度随着高度的增加而增加。而Johnson-Lun 和Johnson-SO 模型组合则相反,颗粒速度随高度的增加而降低,这与图7(b)的固体体积变化趋势正好相反,表明颗粒速度对固体体积的变化十分敏感。不同模型组合的颗粒速度预测值与实验值的平均相对偏差分别为18.2%(BL 模型)、23.4%(JL 模型)和14.1%(JSO模型)。

图9 不同模型组合预测的中央剖面上固体体积分数分布云图Fig.9 Distribution of solid phase volume fraction on central section predicted by different model combinations
一般情况下,在流化床体系中采用Based-Lun模型[26]、而在料仓体系中采用Johnson-Lun 模型[23],这表明模型的选取与体系有关。与本体系实验结果相比,Based-Lun 模型在压降、固体出口质量流率、固体体积分数、壁面区域固体速度等方面的预测值与实验测量值的偏差都较小。综上所述针对本文的气固移动体系,Based-Lun 模型预测得更准确,更能反映实际流动中的气固流动行为。本工作将探究其他模型参数对Based-Lun 模型的影响,进一步优化模型参数设置。
3.3.2 临界固含率 在欧拉多相流模型中涉及许多参数的设定,例如颗粒间恢复系数e、颗粒内摩擦角θ、临界固含率εs,min、最大允许固含率εs,max、初始填充固含率εs,intel等。这些参数既有实验测量值也有经验性参数,颗粒内摩擦角θ由实验测定,最大允许固含率εs,max为实验测得的床层紧密堆积固含率,而临界固含率εs,min是模型考虑颗粒间摩擦作用的临界值,是经验性参数,在许多欧拉模型的设置中会有细微的差别。针对球形颗粒体系的欧拉模型,εs,min一般设为0.5,因此本文在0.47~0.53 范围内考察了临界固含率对模拟结果的影响。图11、图12分别给出了不同εs,min下的压降和固体速度。由图可知,改变临界固含率εs,min,对压降和近前后壁面区域固体流速的影响并不显著。这可能是由于在100~500 mm高度范围内固含率始终大于0.53,导致临界固含率的改变对该区域而言并无明显影响。此外由图12(b)可知,增大临界固含率εs,min能在一定程度上增加固体出口质量流率,这是因为临界固含率的增大使得在出口上方受到摩擦限制的体积边界向外扩展,无摩擦区域变大,出口区域的固体流动更加容易。
3.3.3 内摩擦角 模型采用拟流体化简化了颗粒相的计算,导致模型对固体相流场的预测精度变差。欧根系数修正后,模型误差主要来源于颗粒间摩擦力。内摩擦角是颗粒间摩擦力的主要参数,因而可以通过调控其大小来改变模型计算的颗粒间摩擦力,间接影响颗粒流速。为了探究内摩擦角对欧拉多相流模型的影响,本工作在20°~25°范围内选取了不同的内摩擦角,其预测的压降与固体质量流率结果如图13所示。由图可知,随着内摩擦角的增大,压降逐渐增大,固体流率逐渐减小。这不仅表明改变内摩擦角确实能够修正模型,降低预测误差,同时也证实了模型预测压降偏小的主要原因是模型过低估计了固体颗粒间摩擦力,导致预测的固体流速偏大。此外由图14可知,内摩擦角会直接影响出口上方的固体体积分布,随着内摩擦角的增大,“空腔”形状不断发生变化,从“O”形到“8”形再到“X”形,表明摩擦对颗粒架桥行为有着十分重要的影响。“空腔”形状的变化透露出颗粒架桥从拱状向井筒状转变的趋势,因此很有可能是θ=25°条件所预测的“X”形的固体体积分布具有井筒状的部分特征,更能反映实验中颗粒架桥现象,从而导致固体出口质量流率与实验值更为接近。但必须注意的是,由实验测得的内摩擦角为22°,而模拟过程中内摩擦角为25°时模拟结果更为精确,这表明现有模型在预测密相流动时仍存在缺陷,对固体间摩擦力的估值过低。
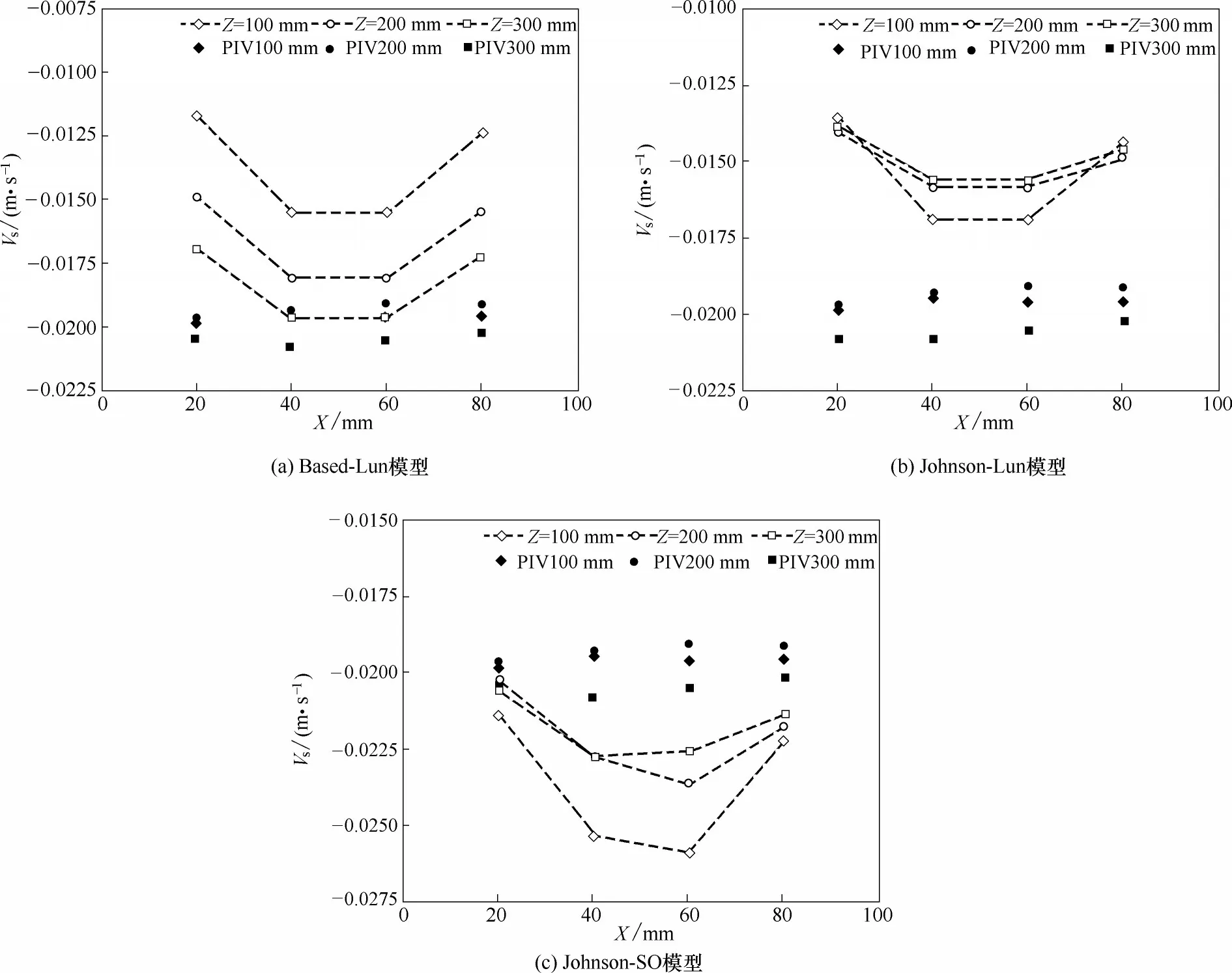
图10 不同模型预测y=1.5 mm处固体速度与PIV测量速度对比Fig.10 Comparison of simulated vertical velocities at y=1.5 mm and velocities measured by PIV
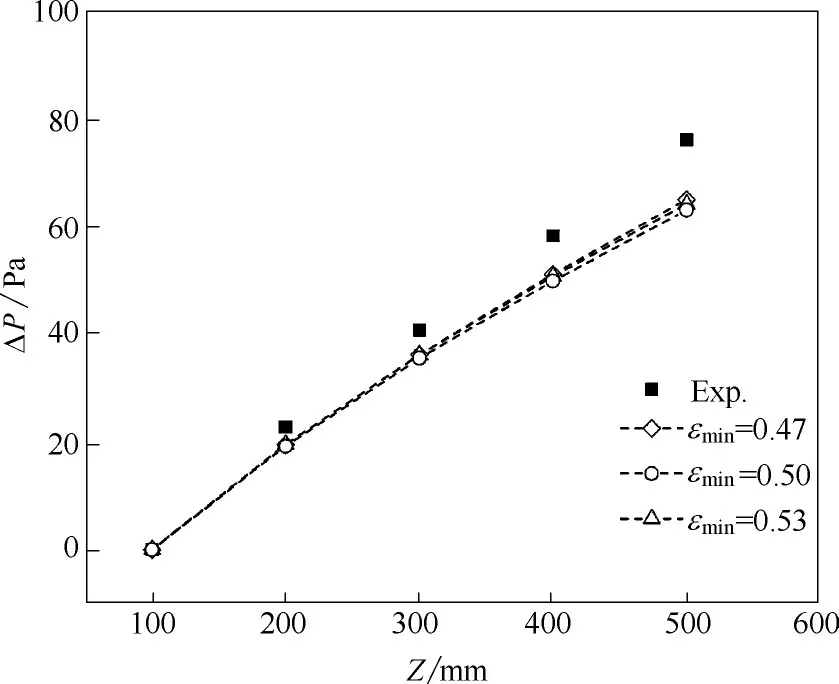
图11 不同临界固含率预测的床层压降轴向分布Fig.11 Axial distribution of pressure drops at different threshold volume fraction for friction
4 结 论
本文在气固移动床中通过欧拉多相流模型,研究了密相气固流动行为。基于实验结果,通过考察常用的摩擦压力模型(Based、Johnson)和径向分布函数模型(Lun、Syamlal O’Brien)等模型,探究了模型的选取以及模型参数变化对预测结果的影响,结论如下。
(1)Johnson 模型预测的固体体积分数低于Based 模型;Syamlal O’Brien 模型预测固体质量流率 远大于Lun 模 型。Based-Lun、Johnson-Lun 和Johnson-SO 三种模型组合都不能准确预测出口上方的固体体积分布,导致固体流动速度被高估。模型在床层压降、固体体积和出口固体质量流率上的相对误差关系为δBL<δJL<δJSO。
(2)根据实验结果修正欧根系数后,模型准确度显著增加,Based-Lun、Johnson-Lun 和Johnson-SO 模型组合的平均压降相对误差分别由68.6%、73.3%和78.2%降低至13.2%、29.7%和42.3%。综合考虑压降、固体出口质量流率、固体体积分数、壁面区域固体速度等结果,认为Based-Lun 模型组合最能反映气固移动床中实际气固流动行为。另外,增加临界固含率εs,min能在一定程度上增加固体出口质量流率,但对高度100~500 mm 范围内的压降和近后壁面的固体速度无明显影响。
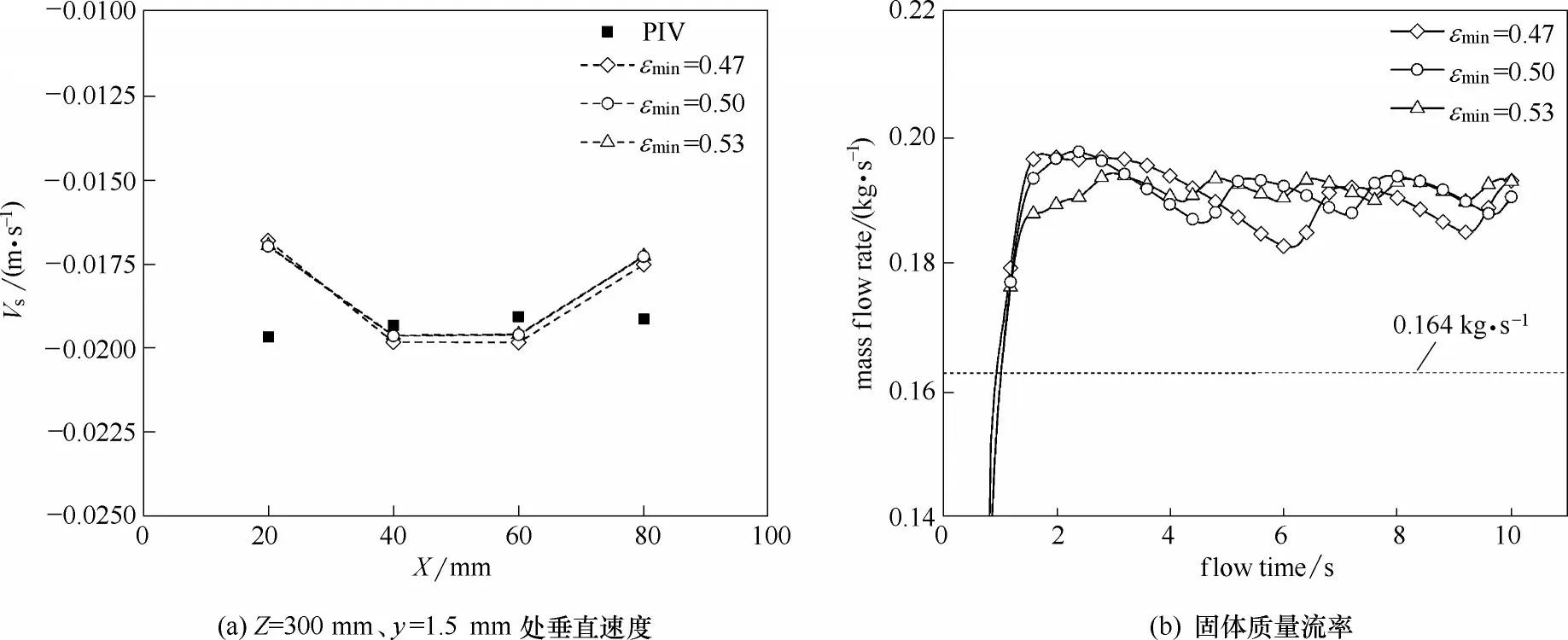
图12 不同临界固含率预测的固体速度分布与质量流率Fig.12 Distribution of vertical velocity and mass flow at different threshold volume fraction for friction

图13 不同内摩擦角预测的床层压降轴向分布与质量流率Fig.13 Axial distribution of pressure drops and solid mass flow rate at different internal friction angles

图14 不同内摩擦角对应的出口上方固体体积分布Fig.14 Distribution of solid phase volume fraction above outlet at different internal friction angles
(3)随着内摩擦角的增大,固体流率逐渐减小,气体压降逐渐增大。这不仅表明改变内摩擦角确实能够修正模型,降低预测误差,同时也证实了模型预测压降偏小的主要原因是模型过低估计了颗粒间摩擦力。此外随着内摩擦角增大,出口上方的架桥形状由拱状向井筒状转变,证明了颗粒间摩擦力对出口上方的架桥现象有着显著的影响。固体质量流率在内摩擦角为25°时与实验测量值误差最小表明现有模型仍存在缺陷,发展新的模拟或者做出基于机理的模型修正极为重要。
