基于L21范数和回归正则项的半监督聚类算法

朱恒东，马盈仓，张 要，张 宁

(西安工程大学 理学院 陕西 西安 710048)

0 引言

传统的机器学习方法一般分为监督学习和无监督学习[1]。传统的监督学习，通常需要大量良好标记样本对模型进行训练，而传统的无监督学习的整个过程不借助监督信息[2]。然而在现实应用中，通常只有小部分数据带有监督信息，这些数据难以支撑传统监督学习，若继续使用传统无监督学习，会浪费这些监督信息[3]。

为了更好地处理监督信息与数据之间的关系，有学者提出了半监督学习[4-5]。按照学习场景的不同，半监督学习通常可以分为半监督聚类和半监督分类[6]。本文主要研究的半监督聚类是通过对有标签数据样本(监督信息)的分析来辅助指导整个聚类过程。根据监督信息形式的不同，半监督聚类分为基于成对约束和基于标签信息的半监督聚类。

成对约束信息一般判断两个数据点是否同属一类[7]。文献[8]提出了一种基于成对约束对的半监督核K-means聚类的图像分割算法，该算法利用随机产生的must-link约束对来初始化中心，结合核K-means聚类的思想，使该算法能对图像进行较为准确的分割。文献[9]提出了基于成对约束的交叉熵半监督模糊聚类算法，这种方法利用样本的交叉熵来表达成对约束信息，能够在成对约束信息较少的情况下实现快速聚类和获得较优的结果。文献[10]提出一种基于密度自适应邻域相似图的半监督谱聚类算法，利用成对约束信息调整谱聚类中相似矩阵，可以从数据全局寻求最优解。

然而相较于成对约束信息，标签信息可以直接判断数据点的类别[11]。文献[11]提出了seeded-K-means算法，将标记样本引入K-means中，其中标记样本作为seeds集，但是难以处理高维数据。文献[12]认为基于线性嵌入的回归模型难以捕获数据流形结构，提出利用Lδ正则项放宽线性约束，使之可以更好学习数据的流形结构，但是增加了Lδ的调参负担。文献[13]在文献[12]的基础上通过增加对标签矩阵的拉普拉斯正则项放宽线性约束，去除Lδ的调参负担，但是过多的正则项使得模型的计算量也随之增加。文献[14]提出了一种半监督迭代多任务回归。通过联合考虑已标记和未标记的数据来学习低维子空间，并通过两个回归任务来连接已学习的子空间，但是算法时间复杂度较高。

半监督聚类算法研究至今，在机器学习[15-16]、图像处理[17-18]、计算机视觉[19]以及系统辨识[20]等领域都有着广泛的应用。针对半监督学习中基于线性嵌入的回归模型难以捕获数据流形结构的问题，本文提出新的算法:首先通过L21正则项构造标签矩阵F的弹性嵌入回归模型；进而借助图正则化思想，利用拉普拉斯正则项调整模型，约束原始空间的数据X与低维空间的数据F流形结构一致；最后通过L21范数的鲁棒性学习得到数据点的相似矩阵，与L2范数和Lδ范数相比，L21范数能很好地消除离群点的影响且没有调参的负担。因此提出基于L21范数和回归正则项的半监督聚类算法(semi-supervised clustering algorithm based onL21norm and regression regular term,SSLC)。

1 相关工作

1.1 半监督学习

给定数据集X={x1,x2,…,xn}∈Rd×n，在半监督学习中，训练数据集中只有少量数据被标记，假设有l个数据点为标记点，记为Xl={x1,x2,…,xl}，未标记点记为Xu={xl+1,xl+2,…,xn}，对于每个数据i，都有对应的标签yi∈{0,1}，其中数据集Xl对应的标签向量为yl∈Rl×1，定义f=[f(l),f(l)]T为预测标签，其中f(l)∈Rl×1和f(u)∈Ru×1，因此我们得到经典半监督学习函数

(1)

其中：W是投影向量；b为偏置向量；1为所有元素为1的向量；α和β为常数。从式(1)可以看出，约束预测的标签f与线性模型XTW+1b完全相等，在实践中，为了减少参数调整的负担，使用了式(2)来避免过拟合，

(2)

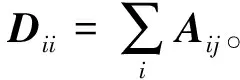
1.2L21范数的引入

使用L2范数的平方作为损失函数对较小的异常值不敏感，但对较大的异常值敏感；使用L1范数作为损失函数对较大的异常值不敏感，对较小的异常值敏感；而使用Lδ范数作为损失函数时，可以通过调整参数δ使其介于L2范数和L1范数之间，则无论异常值是大是小，L2和L1范数的鲁棒性均被利用，但是增加了调整参数δ的负担。为了解决上述问题，通过L21范数[21]，使得聚类模型更好地处理异常值和减少调参的负担，起到弹性嵌入的作用，且没有Lδ范数的调参负担。L21范数为

其中:m是行数;n是列数。

1.3 构造初始相似矩阵

本文为了更好地学习相似矩阵，基于K共享近邻和已知标签矩阵F(l)给出初始相似矩阵A的构造方法如下。

定义1(K近邻[22]) 样本点xi∈X的K近邻为该点到其他样本点的距离中最近的K个点，定义为

KNN(i)={j∈X|index_dist(i,j)≤K}，

(3)

其中：index_dist(i,j)表示样本点xi到其他样本点的距离升序排序后的索引值；dist(i,j)表示两点之间的欧氏距离。

定义2(K共享近邻[23]) 假设样本点xi、xj∈X，KNN(i)为样本点xi的K近邻集，KNN(j)为样本点xj的K近邻集，则样本点xi和xj的K共享近邻集定义为

SKNN(i,j)={KNN(i)∩KNN(j)}。

(4)

根据定义1和定义2，得到初始相似矩阵A的定义为

(5)

其中：Num是SKNN(i,j)中的元素个数；∑dist(xi,SKNN(i,j))是样本点xi到SKNN(i,j)中元素的距离之和。

根据已知标签矩阵F(l)构造约束矩阵为

(6)

其中：若标签Fi和Fj相等，说明xi和xj属于同类，反之亦成立。根据cons矩阵和式(5)，得到最终的初始相似矩阵A为

(7)

2 模型的建立及求解

2.1 模型建立

由于线性函数XTW+1b是通过标签矩阵F学习得到的，考虑到标签矩阵F与学习到的线性模型XTW+1b存在距离，为了更好地学习数据的流形结构，借助L21范数的弹性嵌入作用，建立弹性半监督学习函数

(8)

考虑到算法最后要对F进行聚类，为了约束原始空间的数据X与映射到低维空间的数据F几何结构不变，基于图正则化思想，选择拉普拉斯正则项来调整式(8)，建立目标函数

(9)

其中：拉普拉斯矩阵LS是由给定的相似矩阵A得到的，考虑到随着预测的标签矩阵F(u)的更新，为了保持拉普拉斯正则项的约束不变，与标签矩阵F对应的LS也应该更新。而相似矩阵S可以通过学习初始相似矩阵A得到，由于学习的相似矩阵S与给定的初始相似矩阵A存在距离，通过L21范数的鲁棒性学习一个最优的相似矩阵并完成对LS的更新，调整式(9)为最终目标函数

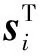
(10)

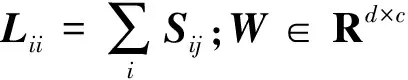
2.2 模型求解

关于2.1节中目标函数式(10)，采用交替迭代优化算法来求解。

① 固定F、W和b，求解S，式(10)就转为

(11)

关于式(11)，根据文献[24]，已知存在fi∈Rc×1，使得式(12)成立，

(12)

(13)

② 根据文献[13]，分别得到b、W、F的更新式为

b=FTU1/1TU1-WTXU1/1TU1，

(14)

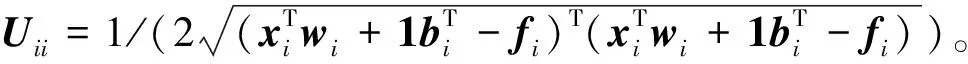
W=(XNXT)-1XNF，

(15)

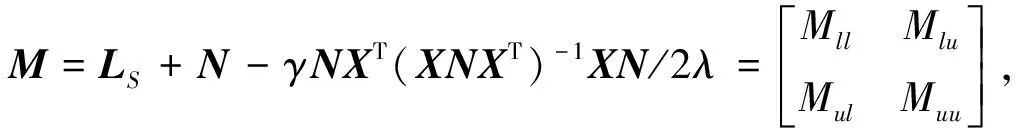
(16)

2.3 算法流程

根据2.2模型求解，SSLC算法流程如下。

输入：X为数据集，F(l)为已知标签矩阵，λ和γ为参数，A为初始相似矩阵。

输出：相似矩阵S，降维后新数据矩阵F，聚类结果y。

1) while 不收敛 do

2) 初始化LS，N；

3) 根据式(16)更新F；

4) 利用更新后的F，根据式(13)求解出S，更新LS；

5) 利用更新后的F，根据式(14)更新W；

6) 利用更新后的F和W，根据式(15)更新b；

7) 利用更新后的F，W，b，更新U；

8) end while

9) 对F进行K-means，完成聚类。

2.4 收敛性证明

定理1算法中的目标函数

minγ‖XTW+1bT-F‖2,1+2λTr(FTLSF)+‖S-A‖2,1，

在固定F、W和b时，交替迭代更新S过程中，目标函数值逐步减小。

(17)

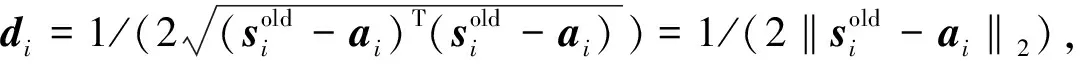
(18)

文献[21]已证明式(19)成立，任意非零向量x,y∈Rc，有

(19)

根据式(19)知

(20)

将式(18)和式(20)相加可得

(21)

将式(21)中的每个i相加可得

(22)

由1.2节的定义可得

γ‖XTW+1bT-F‖2,1+2λTr(FTLSnewF)+‖Snew-A‖2,1≤γ‖XTW+1bT-F‖2,1+

2λTr(FTLSoldF)+‖Sold-A‖2,1。

(23)

因此，该算法收敛。

3 实验分析

3.1 相关算法及参数设置

接下来本文提出的SSLC算法将分别与DAN-SSC算法[7]、SSDC算法[26]、SS-Kernel-Kmeans算法[27]进行比较，以上三个对比算法为半监督聚类算法。使用聚类准确率(accuracy，acc)和兰德指数(rand index，RI)对聚类性能进行评价。测试数据集分别为人造数据集和真实数据集。其中人造数据集选用了具有代表性的Cdata9和Cdata04数据集说明SSLC算法的有效性，真实数据集采用ecoli-uni、vowel、dnatest和isolet_uni数据集进行对比。

其中DAN-SSC算法的参数k为目标聚类数。SSDC算法根据文献[21]建议，取percent=50，D=1。SS-Kernel-Kmeans算法根据文献[22]建议，参数k为目标聚类数，最大迭代次数取120。SSLC算法，参数c为目标聚类数，k=10，参数λ=0.1，γ=1。

表1 两种人造数据集Table 1 Two kinds of artificial data sets

3.2 人造数据集测试及分析

本节选用Cdata04数据集和Cdata9数据集来说明SSLC算法的有效性。这两种不同的人造数据集详细信息如表1所示。图1和图2是测试的结果图。测试中已知标签信息的数据量取值为40%。

图1 Cdata04数据集测试结果Figure 1 Experimental results of Cdata04 dataset

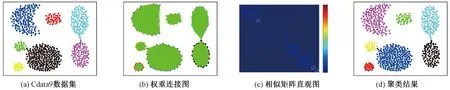
图2 Cdata9数据集测试结果Figure 2 Experimental results of Cdata9 dataset

图1(a)代表原始的Cdata04数据集，是由4个环型簇组成，形状如四叶草，叶子交汇的地方，表示数据之间联系紧密，因此给聚类分析带来了一定的难度。图1(b)是以最终求解出的相似矩阵S为权重，将数据重新连接，虽然相似矩阵类内的相似度保留略多，但是类间的相似度为0。图1(c)是相似矩阵S的直观表示，从图中可以发现，相似度矩阵具有精确块对角矩阵的结构。图1(d)是聚类结果图，数据集划分很好。

图2(a)代表原始的Cdata9数据集，是由7个环型簇组成，簇与簇交汇的地方表示数据之间联系紧密，因此给聚类分析带来了一定的难度。图2(b)是以最终求解出的相似矩阵S为权重，将数据重新连接，虽然相似矩阵类内的相似度保留略多，但是类间的相似度为0。图2(c)是相似矩阵S的直观表示，相似度矩阵具有精确块对角矩阵的结构。图2(d)是聚类结果图，数据集被很好地划分。

3.3 评价指标

在真实数据集测试中，本文将分别采用acc指标和RI指标来评价SSLC算法、DAN-SSC算法、SSDC算法、SS-Kernel-Kmeans算法的效果。

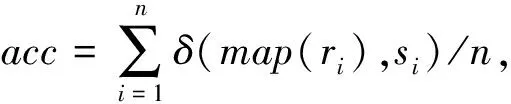
RI:是一种用排列组合原理来对聚类进行评价的方法。计算公式为RI=2(a+d)/n(n+1)，其中：n为样本个数；a表示在真实类别si的数据也隶属于聚类算法结果ri的个数；d表示不在真实类别si的数据也隶属于聚类算法结果ri的个数。RI的结果值在[0,1]之间，值越大越好。

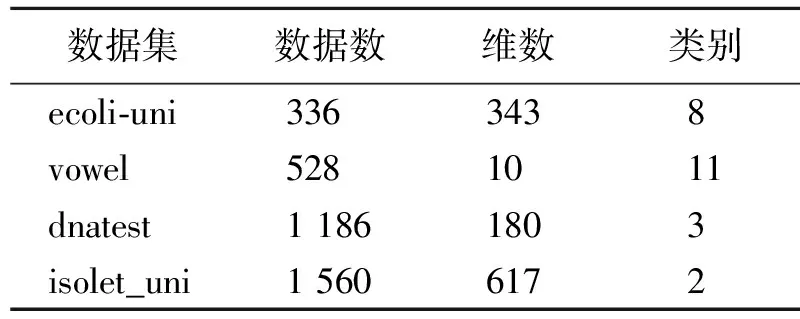
表2 4个UCI数据集Table 2 Four UCI datasets

3.4 真实数据集测试及分析

为了验证算法在真实数据集上的效果，判断算法是否具有实际意义，本节分别采用了UCI数据库中的ecoli-uni、vowel、dnatest和isolet_uni共4个数据集进行测试，它们的详细信息如表2所示。其中4个算法所使用的已知标签信息的数据量取值范围分别为10%、20%、30%、40%、50%、60%。

图3是基于acc指标对聚类算法性能关于UCI真实数据集的评价结果，从图3的(a)、(b)和(c)可以看出，本文提出的SSLC算法是明显好于其他3个聚类算法，图3(d)中SSLC算法初始精度虽然低于SS-Kernel-Kmeans算法，但是随着已知标签数据量的增多，SSLC算法和DAN-SSC算法精度在不断提升，最终在60%处，SSLC算法精度高于SS-Kernel-Kmeans算法。

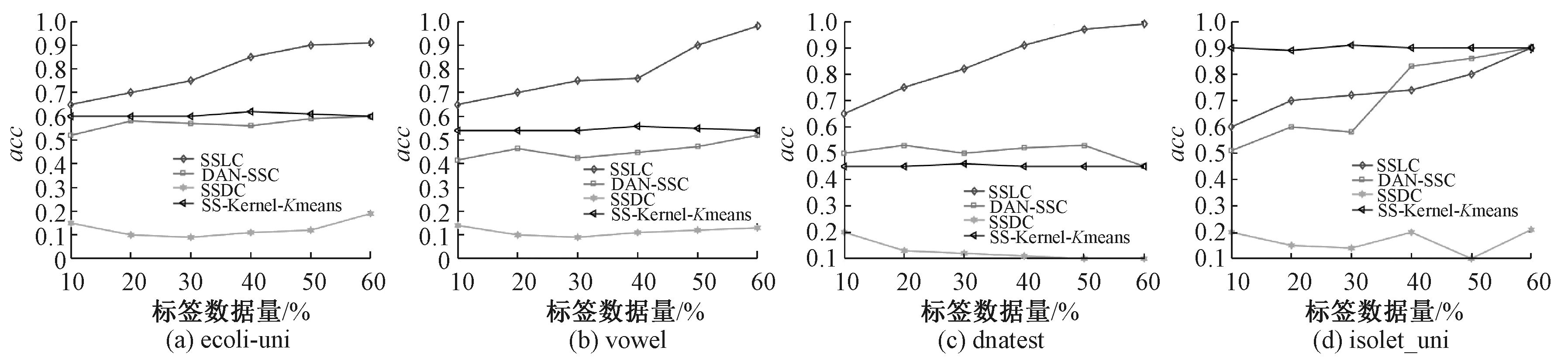
图3 acc指标对聚类算法性能的评价结果Figure 3 Evaluation results of acc on the performance of clustering algorithm

图4是基于RI指标对聚类算法性能关于UCI真实数据集的评价结果，大体上与图3结果相近，但也略有不同。在dnatest数据集中，SSDC算法相对于DAN-SSC算法和SS-Kernel-Kmeans算法的RI指标结果好于acc指标结果；在isolet_uni数据集上，SSLC算法的RI指标性能提升的速度高于acc指标。

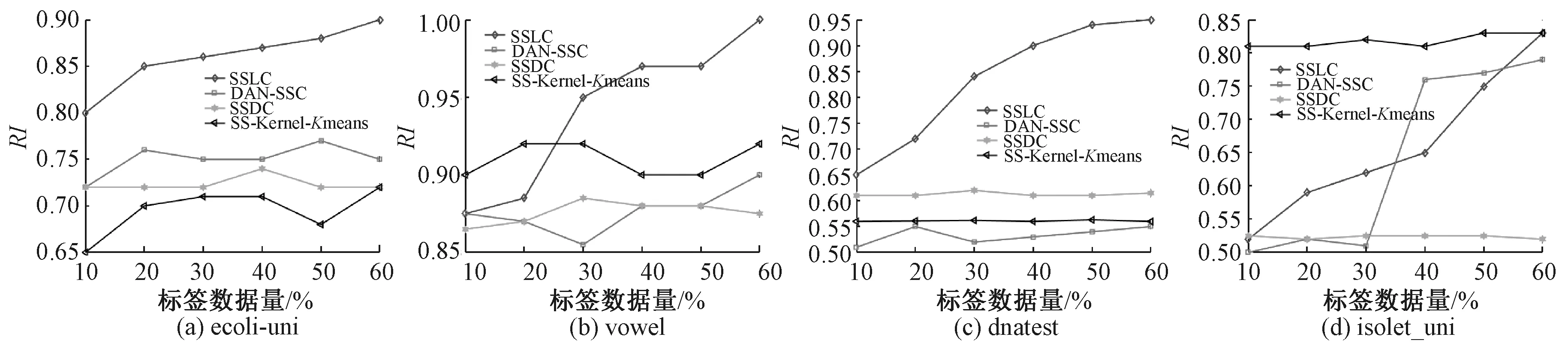
图4 RI指标对聚类算法性能的评价结果Figure 4 Evaluation result of RI index on the performance of clustering algorithm

综上所述，本文提出的SSLC算法随着已知标签数据量的增多，性能也会提高，最后得到很好的聚类结果。实验结果说明本文提出的半监督聚类算法合理，L21范数弹性约束可以使得SSLC更好地学习数据的流形结构，从而构造合理的相似矩阵，最终得到更好的聚类结果。

4 结论和展望

本文概述了半监督学习和半监督聚类的相关研究，一方面借助L21正则项构造半监督回归模型；另一方面利用L21范数的鲁棒性学习合理的相似矩阵，从而改善聚类效果。本文分别在人工数据集上进行试验和真实数据集上进行算法对比试验，结果进一步验证了本文提出的SSLC算法的有效性。SSLC算法的后续研究可考虑在降低已知标签数据量的同时，如何保证其良好的性能及如何与其他聚类算法相结合。