广义正交模糊IOWA算子及其在多属性决策中的应用

杜文胜，闫雅楠

(郑州大学 商学院 河南 郑州 450001)

0 引言

多属性决策是现代决策科学的一个重要组成部分。由于决策环境的复杂性，导致人们对于信息认知和表达的不确定性，决策评价者很难精确地表示决策事物的属性值。文献[1]提出了模糊集理论，可以描述不确定现象。随后，文献[2]对模糊集理论进行了推广，提出了直觉模糊集理论。文献[3-4]定义了直觉模糊集上的加法运算、数乘运算、乘法运算和指数运算。随着模糊理论的发展，模糊信息的适用范围在不断拓宽。美国学者Yager提出了毕达哥拉斯模糊集理论[5]和广义正交模糊集理论[6]。毕达哥拉斯模糊集的约束条件是隶属度与非隶属的平方和不大于1。广义正交模糊集的约束条件是隶属度与非隶属度的q次方之和小于或者等于1。文献[7]提出了一系列广义正交模糊加权算术平均和加权几何平均算子。文献[8]提出了一簇广义正交模糊Bonferroni平均算子。文献[9]提出了一系列广义正交模糊Heronian平均算子。文献[10]提出了一簇广义正交模糊Maclaurin对称平均算子。随后许多专家学者在该领域做出了研究与探索[11-14]。

美国学者Yager首先提出了有序加权平均(ordered weighted average, OWA)算子的概念[15]，并得到广泛应用。随后，Yager又提出了诱导有序加权平均(induced ordered weighted average, IOWA)算子[16]，该算子的特点是权重只与集结过程中的位置有关。自提出以来，IOWA算子在很多研究领域被扩展和应用[17-21]。但是在广义正交模糊环境下的IOWA算子及其应用仍待研究。

本文利用IOWA算子集结广义正交模糊信息，提出广义正交模糊IOWA(q-rung orthopair fuzzy induced ordered weighted average，q-ROFIOWA)算子，并考察算子的性质，将该算子应用在多属性决策问题中，通过实例分析了方法的有效性与稳定性。

1 预备知识

1.1 广义正交模糊集

定义1[6]设X为一个非空一般集合，则定义在X上的广义正交模糊集A的表达式为

A={〈x,uA(x),vA(x)〉|x∈X}，

(1)

图1 各模糊集的隶属度空间范围Figure 1 Membership spaces of different types of fuzzy sets

其中：uA(x)和vA(x)分别表述元素x属于集合X的隶属度和非隶属度，并且满足0≤uA(x)≤1，0≤vA(x)≤1以及0≤uA(x)q+vA(x)q≤1(q≥1)。

为了方便，记α=(u,v)为一个广义正交模糊数。显然，广义正交模糊数的隶属度空间比毕达哥拉斯和直觉模糊的隶属度空间都大，如图1所示。

定义2[7]设α1=(u1,v1)和α2=(u2,v2)为两个广义正交模糊数，并且λ为任意正数，则广义正交模糊数的运算法则为：

定义3[7]设α=(u,v)为一个广义正交模糊数，则α的得分函数定义为S(α)=uq-vq，α的精确函数定义为H(α)=uq+vq。对于任意两个广义正交模糊数α1=(u1,v1)和α2=(u2,v2)，则有：

1) 若S(α1)>S(α2)，则α1>α2；

2) 若S(α1)=S(α2)，则：

若H(α1)>H(α2)，则α1>α2；

若H(α1)=H(α2)，则α1=α2；

若α1>α2或α1=α2，记作α1≥α2。

1.2 诱导有序加权平均算子

定义4[16]设有二元数对〈πi,ai〉(i=1,2,…,n)，称满足下述关系的fω为诱导有序加权平均算子，

(2)

2 广义正交模糊IOWA算子

2.1 基本定义

定义5设αi=(ui,vi)(i=1,2,…,n)为一组广义正交模糊数，若

(3)

则称q-ROFIOWA为广义正交模糊诱导有序加权平均算子。

定义5给出了IOWA算子在广义正交模糊环境下的数学表达式。可以看出，IOWA算子在实数环境与广义正交模糊环境下的数学表达形式是类似的。需要注意的是，在广义正交模糊环境下IOWA算子需要遵循广义正交模糊集的运算法则(定义2)。根据定义2和定义5可以得到如下定理。

定理1设αi=(ui,vi)(i=1,2,…,n)为一组广义正交模糊数，则利用q-ROFIOWA算子集结后的结果仍然是广义正交模糊数，且

(4)

证明首先证明等式成立，再证明集结结果仍为广义正交模糊数。根据定义2可以得到

因此

所以

由于uq+vq≤1，则uq≤1-vq，因此

故算子聚合的结果也是一个广义正交模糊数。

2.2 算子性质

性质1置换不变性

设(〈π1,α1〉,〈π2,α2〉,…,〈πn,αn〉)是任一数据向量，(〈π′1,α′1〉,〈π′2,α′2〉,…,〈π′n,α′n〉)是(〈π1,α1〉,〈π2,α2〉,…,〈πn,αn〉)的任一置换，则

q-ROFIOWA(〈π1,α1〉,〈π2,α2〉,…,〈πn,αn〉)=q-ROFIOWA(〈π′1,α′1〉,〈π′2,α′2〉,…,〈π′n,α′n〉)。

中的βj是相等的，即q-ROFIOWA算子具有置换不变性。

性质2幂等性

设(〈π1,α1〉,〈π2,α2〉,…,〈πn,αn〉)是任一数据向量，若对任意的i有αi=α=(u,v)，则有

q-ROFIOWA(〈π1,α1〉,〈π2,α2〉,…,〈πn,αn〉)=α。

证明由于αi=α=(u,v)对于所有i都成立，根据定理1可得

即q-ROFIOWA算子具有幂等性。

性质3单调性

令αi=(ui,vi)和βi=(si,ti)(i=1,2,…,n)为两组广义正交模糊数，若ui≤si、vi≥ti对于任意i都成立，则有

q-ROFIOWA(〈π1,α1〉,〈π2,α2〉,…,〈πn,αn〉)≤q-ROFIOWA(〈π1,β1〉,〈π2,β2〉,…,〈πn,βn〉)。

证明记q-ROFIOWA(〈π1,α1〉,〈π2,α2〉,…,〈πn,αn〉)=(u,v)和q-ROFIOWA(〈π1,β1〉,〈π2,β2〉,…,〈πn,βn〉)=(s,t)。

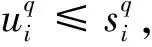
性质4界值性

设αi=(ui,vi)(i=1,2,…,n)为一组广义正交模糊数，则有

α-≤q-ROFIOWA(〈π1,α1〉,〈π2,α2〉,…,〈πn,αn〉)≤α+，

其中：

证明根据性质2可得

q-ROFIOWA(〈π1,α-〉,〈π2,α-〉,…,〈πn,α-〉)=α-,q-ROFIOWA(〈π1,α+〉,〈π2,α+〉,…,〈πn,α+〉)=α+。

根据性质3可得

q-ROFIOWA(〈π1,α-〉,〈π2,α-〉,…,〈πn,α-〉)≤q-ROFIOWA(〈π1,α1〉,〈π2,α2〉,…,〈πn,αn〉)，

q-ROFIOWA(〈π1,α+〉,〈π2,α+〉,…,〈πn,α+〉)≥q-ROFIOWA(〈π1,α1〉,〈π2,α2〉,…,〈πn,αn〉)。

综上可得α-≤q-ROFIOWA(〈π1,α1〉,〈π2,α2〉,…,〈πn,αn〉)≤α+。

3 实例分析

本节用青年创新创业奖金的实例说明q-ROFIOWA算子在多属性决策中的应用。最后将其与其他算子进行比较分析，观察其排序结果是否相同。

3.1 基于广义正交模糊IOWA算子的多属性决策方法

设有一广义正交模糊环境下的多属性决策问题，有m个备选方案xi(i=1,2,…,m)，n个属性集Gj(j=1,2,…,n)，ω=(ω1,ω2,…,ωn)T。设决策者给出的广义正交模糊决策矩阵为R=αij=(uij,vij)m×n，αij=(uij,vij)表示第i个备选方案在第j个属性下由决策者给出的评估值。假设诱导变量为评估值的得分函数，基于q-ROFIOWA算子的多属性决策方法如下。

步骤1标准化决策矩阵。在实际的多属性决策问题中，属性往往分为效益型属性(I1)与成本型属性(I2)两种。因此需要用以下公式对决策矩阵进行标准化。

之后根据q-阶正交模糊数的大小比较规则将诱导变量排序。

步骤2利用q-ROFIOWA算子集结决策矩阵，得到每个备选方案的综合属性值αi。

特别说明的是，在计算时确定权重ω的方法有很多种，这里仅介绍OWA算子常用的正态分布赋权法[22]。徐泽水教授从正态分布出发，提出了离散正态分布，给出了位置权重向量，

(5)

其中：μn代表评价者对第n个指标评分的数学期望；σn代表评价者对第n个指标评分的标准差。

步骤3根据定义3计算每个备选方案的得分函数值，将备选方案排序并进行分析。

3.2 问题描述

假设某公司设立一项青年创新创业奖金，分为3个梯度的金额奖励，每年对本市的3个青年创业团队进行资助,这3个团队记作{x1,x2,x3}。通过层层选拔进入最终评议的3支队伍，有5个属性来评价其项目优劣。属性1表示经营情况(G1)，属性2表示发展潜力(G2)，属性3表示科创能力(G3)，属性4表示社会责任(G4)，属性5表示环境友好(G5)。假设ω=(0.22,0.18,0.25,0.17,0.18)Τ，该项奖金在5个属性下的决策信息以广义正交模糊集的形式给出，如表1所示。

3.3 决策过程

步骤1由于所有属性都是效益型属性，无须对其进行标准化处理。根据定义3广义正交模糊数的得分函数规则(q=3)，将诱导变量排序，得到对应的综合信息决策矩阵，如表2所示。

步骤2由广义正交模糊诱导有序加权平均算子集结决策矩阵，得到不同团队的综合属性值。即

表1 广义正交模糊决策矩阵Table 1 Q-rung orthopair fuzzy decision matrix

表2 综合信息决策矩阵Table 2 Comprehensive information decision matrix

α1=(0.553 5,0.298 0),α2=(0.522 5,0.236 1),α3=(0.625 9,0.367 1)。

步骤3计算综合属性值的得分函数，可以得到

s(α1)=0.143 1,s(α2)=0.129 5,s(α3)=0.195 7。

因此创业团队的排序结果为x3>x1>x2。

根据排序结果可知，应对团队3进行第1梯度的资助，对团队1进行第2梯度的资助，对团队2进行第3梯度的资助。

图2 q-ROFIOWA算子随q变化的决策结果Figure 2 Decision results of the q-ROFIOWA operator changing with q

3.4 参数对排序结果及最优选项的比较

为了考察算子中参数q对排序结果的影响，我们赋予参数不同取值对其得分函数及排序结果进行观察。参数q≥2的取值对结果的影响较大，给广义正交模糊IOWA算子中的参数q赋予不同的值，则得分函数和排序结果如图2所示。

从图中可以看出，随着q的增大，团队的得分值减小，q≥3时，不同的q值得到不同的得分，但是排序结果相同。因此可以得出广义正交模糊诱导有序加权平均算子具有较强的稳定性。

3.5 比较分析

为了验证该方法的优点，将本文提出的多属性决策方法与现有的方法进行对比，这些方法包括文献[7]提出的基于广义正交模糊加权算数平均算子及基于广义正交模糊加权几何平均算子的多属性决策方法，文献[8]提出的基于广义正交模糊Bonferroni平均算子多属性决策方法,以及文献[9]提出的基于广义正交模糊Heronian平均算子的多属性决策方法。利用这些方法解决上述问题的得分函数值和排序结果如表3所示。

表3 利用不同的方法得到的得分函数和排序结果Table 3 Score functions and ranking results obtained by different methods

不同的多属性决策方法具有不同的特点，其中文献[7]的方法没有考虑变量间的相关关系；文献[8-9]的方法可以考虑两个变量间的相关关系；但文献[7-9]的方法都没有区分不同位置之间的权重关系。本文提出的多属性决策方法的特点在于权重值只与集结过程中的位置有关，更适合解决属性较多情况下的实际问题。从表3中可知，虽然不同的决策方法得到的得分函数值不同，但只有基于广义正交加权几何平均算子的多属性决策方法的排序结果为x3>x2>x1，其他方法的排序结果都是x3>x1>x2，与本文的决策结果相同。说明基于广义正交模糊诱导有序加权平均算子的多属性决策方法具有有效性。

4 结束语

本文在IOWA算子的基础上提出了广义正交模糊IOWA算子，同时研究了该算子的4个性质，包括置换不变性、幂等性、单调性和界值性。另外基于q-ROFIOWA算子提出了一种新的解决模糊多属性决策问题的方法，并且分析了不同参数q对决策结果的影响，说明了该算法的稳定性。通过实例以及比较分析，说明了该算子在多属性决策应用中的有效性。