标准模型下抗持续泄漏的基于身份加密方案

谢 鸣

(淮北师范大学 网络与信息管理中心，安徽 淮北 235000)

为解决传统公钥密码系统中的证书管理问题，Shamir[1]于1984年提出了基于身份加密(Identity-based Encryption，简称IBE)的思想，其中用户的身份是其公钥，而用户的私钥则由私钥生成器(Private Key Generator，简称PKG)产生。近年来，已经提出了许多有效的IBE方案[2-5]。但在实际生活中，大多数在理想模型中被证明是安全的加密方案无法抵抗由侧信道攻击引起的密钥泄漏。为形式化侧信道攻击，密码研究人员开始研究泄漏模型，特别是持续泄漏模型[6]，在该模型中，敌手能持续获取方案的秘密内部状态信息。抗密钥泄漏的加密方案最近引起了很多关注。李继国[7]等人针对持续泄漏模型提出了抗持续泄漏的基于身份广播加密方案，并基于双重系统加密技术证明方案是安全的。周彦伟等人[8]给出了一种新的能抵抗持续泄漏的IBE方案，在选择身份安全模型中证明了该方案的安全性。

许多抗泄漏IBE方案只能抵抗选择明文攻击(Chosen Plaintext Attack，简称CPA)。根据基于身份的密钥封装机制(Identity-based Key Encapsulation Mechanism，简称IB-KEM)，我们提出了一种抗持续泄漏的IBE方案，并证明该方案在标准模型中能抵抗选择密文攻击(Chosen Ciphertext Attack，简称CCA)。该方案中使用了强提取器将封装的对称密钥随机化，并使用允许泄漏的封装对称密钥对消息进行加密。同时该IBE方案提供了一个私钥更新算法来容忍持续泄漏。

1 预备知识

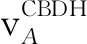
根据定义2以及Goldreich-Levin定理，针对Goldreich-Levin核心谓词f:GT×{0,1}μ→{0,1}，其中μ∈N，有如下引理。

引理1：令A,B,C∈G,u∈{0,1}μ,K=f(T,u)，令K'∈{0,1}是随机选取的。假设存在一个PPT算法B以不可忽略的优势区分分布Δ=(D,K,u)和Δrand=(D,K',u)，则存在一个PPT算法在输入D=(g,A,B,C)前提下，以不可忽略的优势计算出T，从而攻破CBDH问题。

定义3：最小熵 一个随机变量X的最小熵是H∞(X)=-log(maxxP[X=x])。

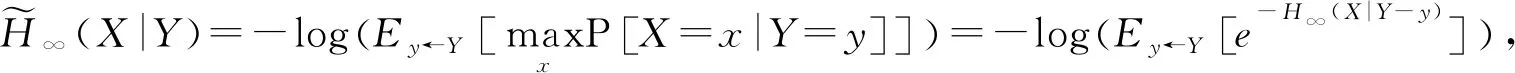
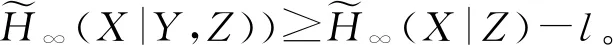
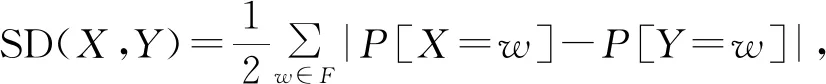
2 抗持续泄漏IBE方案框架及安全模型

2.1 抗持续泄漏IBE方案框架

该框架包含以下五个算法，其中增加了UpdateSK算法来更新私钥，具体内容如下。

初始化算法Setup：输入安全参数1λ(λ∈N)，产生主公钥mpk和主私钥msk。

私钥生成算法KeyGen：输入mpk，msk以及身份ID，输出私钥skID。

加密算法Enc：输入mpk，ID以及消息M，返回一个密文C。

解密算法Dec：输入skID和C，返回M或者终止符⊥。

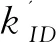
2.2 抗持续泄漏IBE安全模型

参照文献[6-8]，形式化定义了一个IBE持续泄漏安全模型，通过游戏CL-sID-CCA(Continual Leakage，Selective-Identity and Adaptively Chosen Ciphertext Attack)来描述我们的IBE方案能抵抗选择身份、持续泄漏和自适应选择密文攻击。挑战者Ch创建一个列表Lsk以存储形式为(ID,skID)的元组，Lsk在游戏初始化时为空。

初始化阶段：敌手A把身份ID*发送给挑战者Ch。

启动阶段：挑战者运行Setup算法并返回mpk给A。

第一阶段：敌手A能自适应地进行以下询问。

私钥询问：针对身份ID(ID≠ID*)的私钥询问，挑战者在列表Lsk中查找元组(ID,skID)。如果不存在，Ch运行KeyGen算法并输出私钥skID，并把(ID,skID)添加到列表Lsk中。

泄漏询问：Ch创建一个包含元组形式为(ID,K,cnt)的列表Lleak，其中K表示用于加密消息的对称密钥，cnt∈N是一个计数器。Lleak在游戏的初始化阶段为空。Ch从Lleak中查找(ID,K,cnt)，若其不存在，Ch把(ID,K,0)加入列表Lleak中。若该元组存在，Ch判断是否cnt+li≤l，其中i∈N。若判断为假，则输出⊥。否则，对应的(ID,K,cnt)中设置cnt←cnt+li并返回fi(K)，其中fi:GT→{0,1}li为泄漏函数。

解密询问：给定ID，Ch运行KeyGen算法并输出私钥skID。Ch运行Dec算法，使用skID解密密文C，并把明文发送给A。

挑战阶段：A选取两个同样尺寸的消息M0，M1发送给Ch。Ch随机选择一个值β∈{0,1}，加密消息Mβ并返回挑战密文C*=Enc(params,mpk,Mβ,ID*)给A。

第二阶段：A继续做与第一阶段同样的询问，但有一个限制，A不允许对(ID*,C*)进行解密询问。

猜测：A返回猜测β'∈{0,1}。如果β'=β则称A赢得了该游戏。

3 抗持续泄漏IBE方案

下面提出一种新型的抗持续泄漏IBE方案，我们使用强提取器技术以及n-bits基于身份密钥封装机制(IB-KEM)[9]来构造方案。

解密正确性验证如下：

4 安全性证明

定理1若CBDH问题是困难的，则提出的方案在敌手A攻击下是CL-sID-CCA安全的。

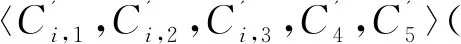
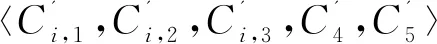
游戏3：游戏3和游戏2除了这种情况(K*∈{0,1}nv是随机选择的，其中n,v∈N)之外都相同。K'*是均匀随机的值。由于K*和K'*均是随机选择的，故可得Pr[E3]=1/2。

基于CBDH问题，可以推出|Pr[E2]-Pr[E3]|≤negl(λ)。该结论可以通过混合论证推出。首先定义一系列游戏：游戏(0),…,游戏(n)，且游戏(0)和游戏2相同，游戏(n)和游戏3相同。下面判定基于CBDH问题游戏(i)与游戏(i-1)是不可区分的(其中i∈[1,n])。由于游戏(0)与游戏2相同，则对于i(从1到n)，第一个K*的iv比特在游戏(i)中设置成随机的，剩下的则和游戏(i-1)中的相同。因此游戏(n)和游戏3相同。令Wi表示在游戏(i)中敌手A输出β'使得β'=β的情况。假设|Pr[W0]-Pr[Wn]|=1/poly'(λ)(其中poly'(·)表示一个多项式函数)，即敌手A在游戏(0)的优势(该优势与在游戏(n)中的一致)是不可忽略的，则一定存在一个值i使得|Pr[Wi-1]-Pr[Wi]|=1/poly(λ)成立。

假设|Pr[W0]-Pr[Wn]|=1/poly'(λ)成立，下面基于CBDH问题构造一个算法B用来区分在引理1中的Δ和Δrand。B输入挑战Λ=(D,R,u)(其中R或者是一个{0,1}v中的随机数或者是一个由f(T,u)输出的v比特串)，则算法B猜测下标值j∈[1,n]使得|Pr[Wj-1]-Pr[Wj]|=1/poly(λ)的概率至少是1/n，且与敌手A做如下交互。

初始化阶段：敌手A发送挑战身份ID*。

第一阶段：下列谕言询问是敌手A进行的自适应询问。

泄漏询问：B创建一个包含元组形式为(ID,K,cnt)的列表Lleak，其中K表示用于加密消息的对称密钥，cnt∈N是一个计数器。Lleak在游戏的初始化阶段为空。B从Lleak中查找(ID,K,cnt)，若其不存在，B把(ID,K,0)加入列表Lleak中。若该元组存在，B判断是否cnt+li≤l，其中i∈N。若判断为假，则输出⊥。否则，对应的(ID,K,cnt)中设置cnt←cnt+li并返回fi(K)，其中fi:GT→{0,1}li为泄漏函数。

解密询问：已知〈ID,Ci,1,Ci,2,Ci,3,C4,C5〉，B做如下操作：如果IDID*，B运行KeyGen算法生成私钥skID，并运行Dec算法使用skID解密密文。

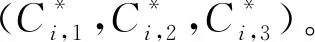
第二阶段：A持续地进行与第一阶段相同的询问，但A不能对(ID*,C*)进行解密询问。

结语

本文给出了IBE方案的形式化定义和安全模型，构造了一个能抵抗持续泄漏的IBE方案，该方案在标准模型中是CCA安全的。在证明过程中，将IBE方案的安全性规约到计算双线性Diffie-Hellman困难问题。抗泄漏的密码学方案设计是一个新的研究方向。我们将进一步研究某些具有更强抗泄漏性能的IBE方案，如随机数泄漏，事后泄漏等；另外，基于格困难问题等构造安全的IBE方案也是一个值得研究的方向。