应用有界度圆填充逼近共形映射
2020-11-18黄宝勤刘太河
黄宝勤 刘太河
(1、2.安顺学院数理学院,贵州 安顺561000)
0 引言
圆填充是在给定边界内对圆的一种排列,使它们没有重叠,并且其中一些(或全部)是相切的。文献[1]应用内部不相交的六边形圆填充来逼近Riemann映射,文献[2]研究了圆填充及其应用,文献[3]对内部可以重叠的圆的排列所组成的圆模式进行了研究。文献[4]应用内部不相交的六边形圆填充来逼近两个单连通区域之间的共形映射,文献[5]对有界度圆填充逼近进行了研究。本文将应用有界度圆填充(度数为6)逼近两个不同单连通区域之间给定的共形映射。令Ω是一个有界单连通区域,P是几乎填满的一个有界度圆填充。假设P的所有缝隙都是三角形,则由圆填充理论知,存在几乎填满单连通区域且与P同构的一个有界度圆填充。共形映射f的逼近解可以通过圆的对应关系来进行构造,逼近解在对有界度圆填充的进行适当规范化后收敛于共形映射函数f:Ω→Ω′,当m(P)→0,其中m(P)=max{在P中圆的半径}。本文分三个部分:第一节介绍与有界度圆填充有关的一些结论,接下来一节构造共形映射的逼近解,最后一节证明这些逼近解收敛于共形映射f:Ω→Ω′,当m(P)→0。
1 预备知识
在常曲率曲面上的一个圆填充P称为是有界度圆填充,如果在P内的每个圆有至多d个邻域圆。特别地,如果在P内的每个圆有六个邻域圆称圆填充P为六边形圆填充。在本文中始终假设有界度圆填充P的所有缝隙都是三角形,并且对于任何圆填充P要求m(P)≤ε,其中ε是某个正常数。
引理1 令Δ(或Δ′)是由半径为R1,R2,R3(或r1,r2,r3)的三个相切圆的圆心组成的三角形,令F是映Δ到Δ′上的一个线性变换,则存在常数π/38 应用该结果可得 (|a|+|b|)另一方面由不等式|z1+z2|≤|z1|+|z2|可得 r1+r2=|F(0)-F(R1+R2)|≤(R1+R2) (|a|+|b|), r1+r3=|F(0)-F((R1+R3)ω)|≤(R1+R3)(|a|+|b|), r2+r3=|F(R1+R2)-F((R1+R3)ω)| ≤(R2+R3)(|a|+|b|) 由此得出 (1) 三角形Δ与Δ′的面积分别为[R1R2R3(R1+R2+R3)]1/2与[r1r2r3(r1+r2+r3)]1/2。因此,线性变换F的行列式一定是 |a|2+|b|2=B (1)式与上式结合,得 (2) 由(1)式,(2)式可得 (3) (4) 对(3)式,(4)式分别应用介值定理知,分别存在常数π/38 成立。从而完成引理证明。 引理2 假设c是有k个邻域圆c1c2,…,ck(k≤d)的半径为r(c)的圆盘,则 证明 令O与O′分别表示圆盘c与cj(j=1,2,…,k)的中心,并且令∠OjOOj+1=θj。下面将要证明 (5) 不失一般性,考虑圆盘c,c1,c2,令OD表示三角形ΔO1OO2内切圆D的中心,并假设∠OO1OD=α,∠OO2OD=β,则有 从而有 这就完成引理的证明。 设T是一个有界度的三角剖分其承载形是一个紧致加边曲面,三角剖分T上的半径函数r是定义在T顶点上的一个正函数。三角剖分T的内部顶点vk的半径函数r的曲率定义如下:设(vk,v1,vm)是与三角剖分T相伴的每个面的顶点,r(vk),r(v1),r(vm)是由欧氏三角形(vk,v1,vm)的顶点为中心所确定的三个相切圆的半径,沿相应的边缘焊接这些三角形可以组成一个锥流形。对于所有以vk为顶点的面,设θ1,θ2,…,θn是对应每个欧几里得三角形中以为顶点vk的角。则kr(vr)=2π-(θ1+θ2+…+θn)是半径函数r在顶点vk上的曲率。当在T的所有内部顶点v都满足Kr(v)=0时,那么我们就说半径函数r是平坦的。 对于单连通的承载形T,则一个平坦的半径函数r确定在刚体运动下的有界度圆填充浸入是唯一地。复平面C内的有界度圆填充浸入,如果所有圆盘的内部都不相交,就称为一个有界度圆填充嵌入。 对于q1≥1,定义σn(q1)是最小的实数使得 对于所有的有界度圆填充浸入P成立,并满足 对于q2≥1,定义σn(q2)是最小的实数使得 对于所有的有界度圆填充浸入P′成立,并满足 有下面的结论 引理3 对于固定常数q1≥1,q2≥1,当时n→∞时,σn(q1)→0,σn(q2)→0。 由引理3知,对于 有下式 成立,并且当n→∞时,σn(q)→0。 令Ω是一个有界且包含固定点ω1,ω2的单连通区域。在∂Ω上给定的正连续函数ρ,有界度圆填充的一个序列构造方法如下:假设平面内有界度圆填充P的最大圆半径为ε(ε为大于零的充分小常数),以最接近ω1的圆c0作为起点,由P的圆组成的链,且每条链内的所有圆的邻域圆都在Ω的内部。出现在这样的链内的所有圆组成并且每个圆至少是这些圆中一个圆邻域的集合记为Cε。令平面区域三角剖分Tε是由连接Cε内所有相切圆的中心而得到的。 在Tε的边界顶点上定义与ρ相伴的函数β方法如下:假设ξ是∂Ω上最接近υ的一个点,当υ是Τε的边界顶点时,定义β(υ)=ερ(ξv)。因为Ω是单连通,由文献[4]的定理1知,单连通区域的Ω一个有界度圆填充P′确定一个平坦半径函数。对于Tε内最接近ω1,ω2,的顶点v1,v2,对P′进行满足P′(v1)中心在原点、P′(v2)的中心在正实轴上的规范化。假设相伴的半径函数为rε。 其中π/38 证明 由引理1知下列两式成立, (6) (7) 其中常数π/38 当n→∞时,σn(q)→0。从而方程(6),(7)可简化为 故引理成立。 令Ω是一个有界,包含固定点ω1,ω2的单连通区域。假设f:Ω→Ω′是满足f(ω1)=0,f(ω2)>0的共形映射,使得|f′|可连续地扩充到Ω的边界上并且在∂Ω上与ρ一致。 (8) 成立。 通过规范化使ω1及ω2分别趋近于0和正实轴就证明了H=f。故定理成立。 本文证明了对于一个有界单连通区域Ω内半径不相等的有界度圆填充(度数为d≥6),存在几乎充满单连通区域Ω′一个同构的有界度圆填充,可以构造共形映射f的逼近解,经过有界度圆填充的适当规范化,逼近解收敛于共形映射函数f:Ω→Ω′,当m(P)→0,其中m(P)=max{在P中圆的半径}。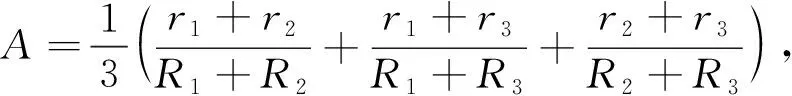

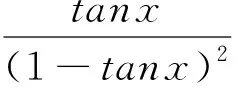
2 构造共形映射的逼近解




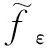
3 收敛性
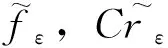

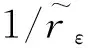
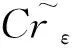
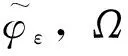
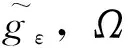
4 结论
