基于模糊理论的链式弹仓自适应滑模控制
2020-11-16韩乃玉李志刚岳才成
韩乃玉,李志刚,岳才成
(1.南京理工大学 机械工程学院,江苏 南京 210094;2.中国北方工业有限公司军贸技术研究院,北京 100053)
在各种机械传动方式中,链传动因其结构紧凑、在恶劣的工作环境中也能保证系统动力传递的可靠性[1],所以自行火炮的弹仓传动系统大多采用链传动。在链式弹仓系统的位置跟踪控制过程中,由于存在较大的啮合冲击以及显著的多边形效应,最终导致了弹仓系统模型中存在非线性项和不确定性[2-3],所以采用传统的控制手段难以实现弹仓系统的高精度位置控制。滑模控制因其对系统模型参数变化和外界干扰不敏感,所以常被用于非线性控制系统[4-5],然而由于不连续切换特性所导致的抖振现象成为滑模变结构控制在实际系统中应用的突出问题。自适应控制能够有效估计系统不确定性因素的界限,为滑模切换项设计合适的自适应律使切换项连续化,能够有效削弱系统的抖振现象。文献[6]采用积分型滑模面设计的自适应鲁棒滑模控制系统,减小了系统的到位稳态误差;针对机械手系统中存在的未建模动态特性,文献[7]基于扰动观测理论提出了一种自适应滑模控制算法,保证了机械手到位的快速性和准确性。模糊控制作为一种现代智能控制策略,因其控制方式简单灵活易于实现且不需建立精准的系统数学模型而被各国科研人员密切关注。文献[8-9]基于模糊万能逼近理论,在未知系统模型的情况下实现了对一类伺服系统的有效控制。
在对自适应滑模控制理论、模糊控制理论研究的基础上以及参考文献的启发作用下,笔者针对存在未建模非线性特性以及不确定性强干扰作用下的链式弹仓回转控制系统,提出了一种自适应模糊滑模控制方法。该方法构造的模糊系统实现了对链式弹仓模型中未知非线性函数的有效估计;此外,算法中设计的自适应滑模切换增益不仅保证了系统的滑模条件,提高了系统的鲁棒性,而且有效削弱了系统的抖振。笔者预先设定了系统的期望角位移轨迹曲线,取角位移以及角速度作为系统状态变量,设计行之有效的控制器,使存在未知非线性函数的链式弹仓系统,在受到不确定的外界干扰的状态下也能比较准确的跟踪所给定的轨迹曲线。
1 链式弹仓系统的数学模型
弹仓系统主要由弹仓本体、弹链以及链传动系统等部件组成,如图1所示。
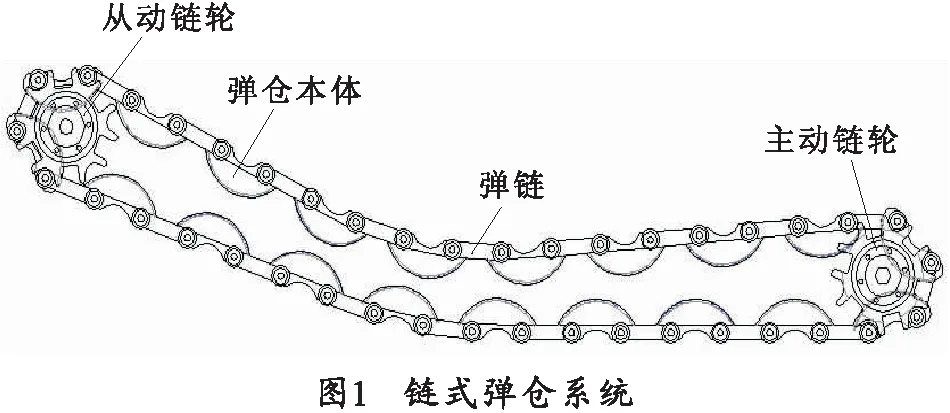
链式弹仓系统由交流伺服电机驱动,由于永磁同步电机的电气时间常数远远小于机械时间常数,所以忽略伺服电机内部电流环的动态特性,将弹仓系统各部件包括减速器、机械构件本体以及传动链轮等的基本物理量等效至电机输出轴上,并对交流伺服电机采用id=0的矢量控制法,得到链式弹仓系统数学模型:
(1)
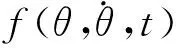
2 控制系统的设计
2.1 模糊系统的设计
依据模糊系统的万能逼近特性[10],取角位移与角速度为模糊系统的输入变量并分别设计5个模糊集,则模糊系统共有25条模糊规则。具体步骤如下:

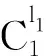
其中,Cl1l2为输出模糊集;j=1,2,…,25;x=[x1,x2].
3)采用乘积推理机,单值解模糊器求解模糊可调参数向量,采用平均解模糊器得到模糊系统输出为
(2)
式中,ξ=[ξ1,ξ2,…,ξ25]T为模糊基向量,且有
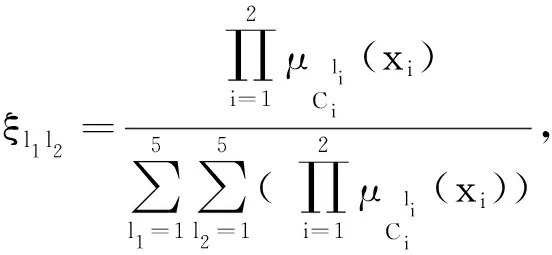
(3)
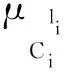
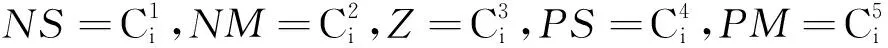

2.2 自适应滑模系统的设计
定义链式伺服系统位置跟踪误差为
e=θ-θd,
(4)
式中,θd为理想位移轨迹曲线。
设计滑模切换函数为
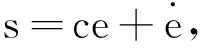
(5)
式中,c>0,为待设计的滑模面参数。

(6)
根据模糊逼近理论,所设计的模糊系统在逼近未知函数的过程中存在一个最优参数α*,使得模糊系统输出一个最优估计函数f*:
f*=α*Tξ,
(7)
(8)
式中,Ω为α的集合。
则有
f=α*Tξ+ε,
(9)
式中,ε为模糊系统的逼近误差。
将式(2)与式(9)作差得
(10)
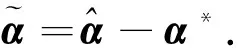
定义Lyapunov函数为
(11)
式中,γ>0,结合式(6)则有
(12)
设计控制律为
(13)
式中:滑模切换增益σ>|ε|max+|Td|max;sgn(s)为符号函数。
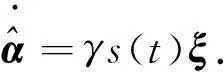
(14)
(15)
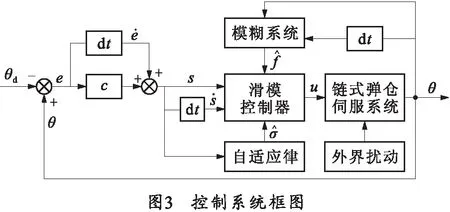
整个系统自适应滑模-模糊控制系统框图如图3所示。
设计自适应律如下:
(16)
式中,γ1>0.
定义新的Lyapunov函数为
(17)
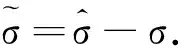
对Lyapunov函数求导,并结合式(13)、(14)、(15)得:
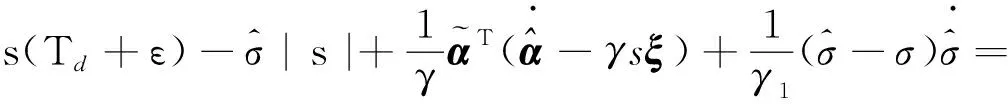
(18)

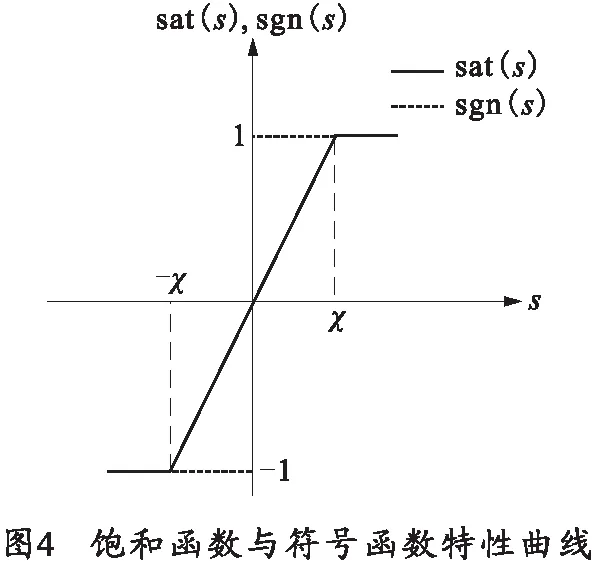
为了消除符号函数的继电器特性[11],改善弹仓回转运动控制过程,采用饱和函数sat(s)代替符号函数sgn(s),则有
(19)
(20)
式中,χ为饱和函数边界层厚度参数,具体两函数特性曲线如图4所示。
3 仿真验证与分析
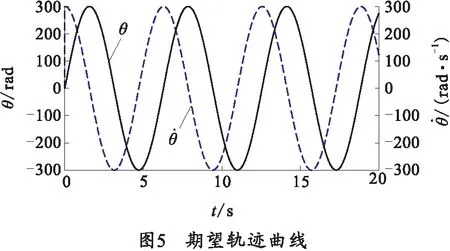
在实际工程中,链式弹仓系统的位移轨迹曲线为点到点的位置控制,而此处为了验证笔者所设计的控制算法的动态跟踪性能,采用正、余弦波曲线分别作为系统的伺服电机转子的角位移、角速度的理想轨迹曲线,如图5所示。角位移最大值为300 rad,周期为2π;角速度最大值为300 rad/s,周期为2π.
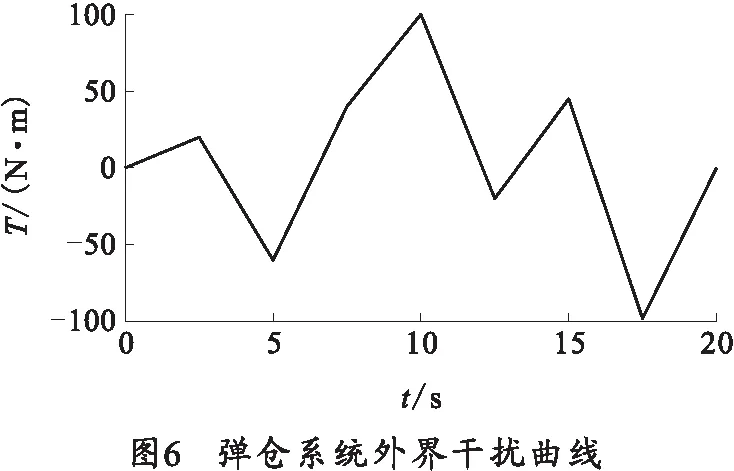
通常情况下,弹仓系统的外部干扰力矩为未知的时变函数。为不失一般性,为弹仓系统设置了幅值为100 N·m时变的外界干扰力矩函数(由于弹仓电机减速器的传动比为100,所以实际等效至电机输出端的干扰力矩的幅值为1 N·m),具体的干扰力矩特性曲线如图6所示。
采用三维软件对弹仓系统建立虚拟样机,将模型导入ADAMS中分析,得到链式弹仓系统的等效转动惯量J=3.79×10-3kg·m2.
所设计的基于模糊逼近理论的自适应滑模控制算法的具体参数设置如下:电机力矩常数kt=0.072 N·m/A;系统隶属度函数参数:a0=150,a1=300;滑模参数:c=100;模糊系统自适应参数γ=0.8;滑模增益自适应参数γ1=0.5;χ边界层厚度参数为0.35;取模糊系统可调参数初始向量为零向量,即α0=[0,0,…,0],取初始滑模增益σ0=0.
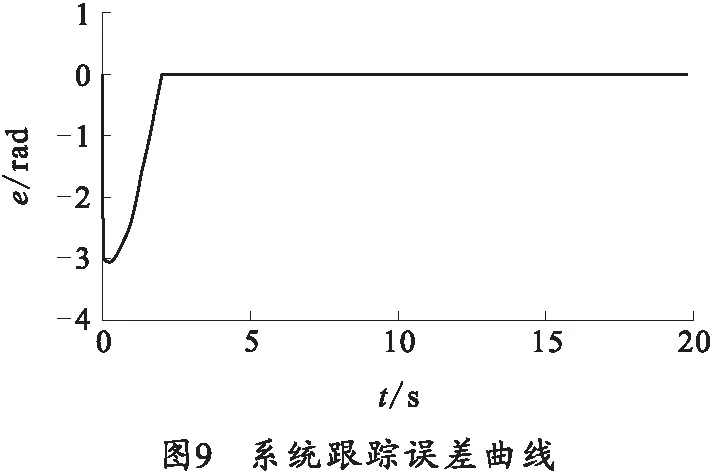
将ADAMS中得到的动力学模型导入MATLAB/Smiulink中搭载仿真环境,依据所设计的算法编写链式弹仓伺服系统的位置控制程序,在scope模块中得到仿真结果曲线,如图7~11所示。
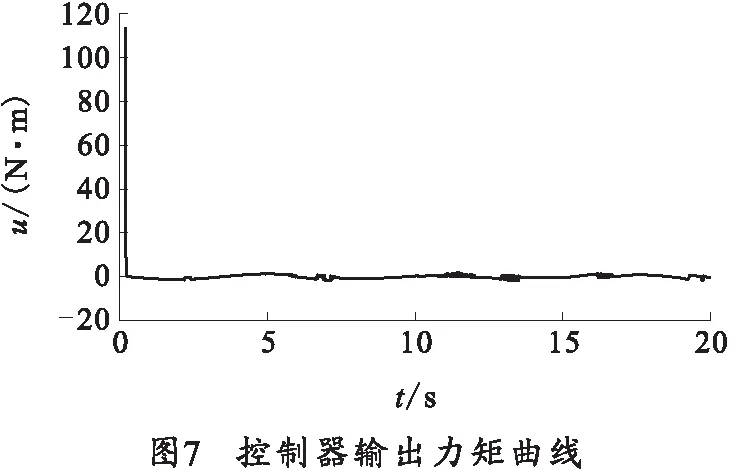
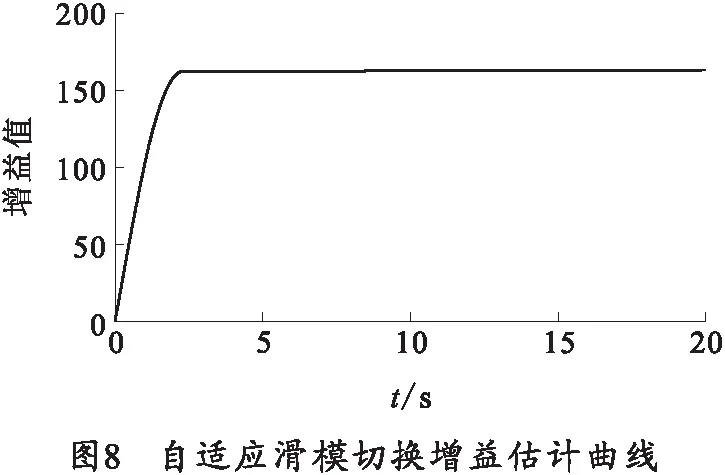
分析仿真结果,从图7可以看出在系统的启动阶段,控制量存在超调现象,由于时间极端所以可以忽略其对系统的影响;系统在较短时间内控制力矩就稳定维持在合理范围内,且控制量无明显的抖振现象。图8则验证了笔者所设计的滑模增益自适应律的有效性。
由图9系统的跟踪误差变化曲线可以看出,在模糊系统自学习阶段(大约2 s的时间)系统有较大的位置跟踪误差但仍在系统允许的误差范围内。当模糊系统完成对未知非线性函数的逼近之后,系统跟踪误差迅速收敛至很小的范围内,所以,总体来说系统具有较高的位置控制精度。
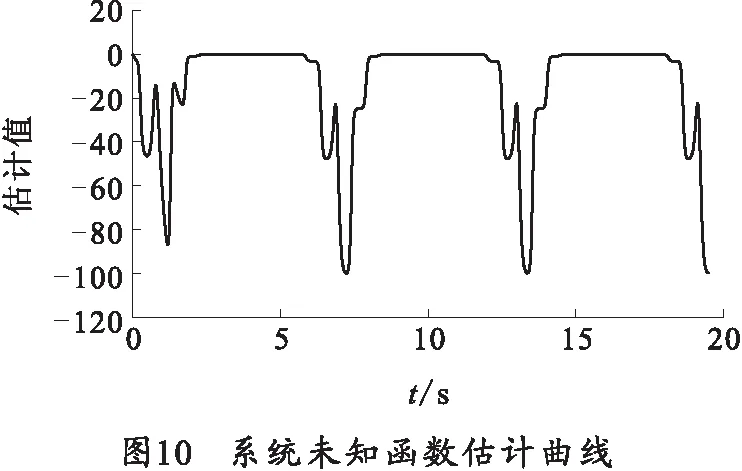

由图10、11可得:由于所设计的模糊逼近系统为开环系统,而且弹仓系统中存在的扰动项与未建模项可以相互转化,所以导致模糊逻辑系统的逼近精度不高,但仍在一定程度上减小了弹仓系统的不确定性。最后,自适应滑模控制补偿了模糊系统的逼近误差,保证了弹仓系统的位置控制精度,实现了对预期轨迹的跟踪。
4 结束语
笔者所设计的一种基于模糊理论的链式弹仓自适应滑模控制,通过构造合理的模糊逼近系统,实现了对存在未知特征量的链式伺服回转系统较好地位置控制。其中,构造的模糊系统降低了弹仓系统模型的不确定性。在此基础上,笔者设计的自适应滑模控制器不仅消除了模糊系统的逼近误差保证了系统的滑模条件,而且削弱了滑模控制的抖振现象。
对设计的控制算法在虚拟的链式弹仓伺服系统中进行仿真验证,结果表明该算法不仅实现了对链传动弹仓伺服系统较为精准的位置控制,而且对外界干扰具有较高的鲁棒性。
