带状变燃速发射药对无后坐力炮内弹道性能影响研究
2020-11-16薛百文涂炯灿昝博勋
薛百文,马 营,涂炯灿,昝博勋
(1.中北大学 机电工程学院,山西 太原 030051;2.重庆红宇精密工业有限责任公司,重庆 402760)
现代战争要求反坦克武器不仅具有威力,而且还应具有良好的机动性。对于步兵反坦克武器,轻量化、小型化是其发展趋势。火炮系统即是坦克武器的主要进攻手段,同时也是反坦克武器的主要反击手段。对于传统的火炮系统,威力与机动性存在矛盾的关系。为了提高机动性,需要降低火炮系统威力。为了解决这种矛盾,国内外学者对多种反后坐装置进行研究。
何永等对二维后坐技术[1-2]和曲线后坐技术[3]进行了研究;David Carlson J 对电(磁)流变技术[4]进行了研究,通过对电流液的控制达到减小火炮后坐力的作用;减小后坐技术还有前冲技术[5-6],其中又包括软后坐技术、待发状态发射技术。肖俊波等提出并设计了新型时延式喷管气流反推减后坐装置[7]。在各种反后坐技术中,发展成为便携式步兵装备,而且成熟可靠,目前只可能是无后坐发射技术。
无后坐炮炮尾处装有拉瓦尔喷管[8]。无后坐力炮发射原理类似于火箭推进的原理[9],通过炮尾端的拉瓦尔喷管产生向前的推力,抵消后坐力。弹丸发射时,膛内火药气体一部分推动弹丸向前运动;另一部分通过尾喷管向后喷出。
射击时,膛内火药气体一方面推动弹丸前进,另一方面又从后方喷管流出,前者使火炮产生后坐力,后者使火炮产生反后坐力。若设计出适当的喷口大小,则向前推动弹丸的气体和经喷管流出的气体在发射时所产生的动量可相互抵消,从而实现火炮发射无后坐。为了减低无后坐力炮的膛内最大压力同时增大初速,采用变燃速发射药。
变燃速发射药在理论上具有先进性和实践上的可实现性,是对传统固体发射药的概念和范畴的突破[10-12]。变燃速发射药具有独特的燃气生成规律[12],通过对火药参数合理的设置,控制燃气生成规律,能提高内弹道性能。笔者通过建立基于变燃速发射药的无后坐力炮内弹道数学模型,分析发射药内外层燃速比、密度比以及外层与总厚度比对最大膛压、炮口初速、不平衡冲量的影响。
1 发射药燃气生成规律数学模型
1.1 基本假设
带状变燃速发射药分内层和外层,设初始长度为2b1,初始宽度为2c1,内层厚度为2e1,外层厚度2e0,具体结构如图1所示。 假设带状变燃速发射药在燃烧过程中燃速满足几何燃速规律。假定带状变燃速发射药燃烧过程分为两个阶段:第1阶段为低速燃烧的外层药与高速燃烧的内层药同时燃烧,而且假设外层发射药侧面与内层发射药有相同的燃烧速率;第2阶段为外层发射药燃完,内层高燃速发射药单独燃烧。
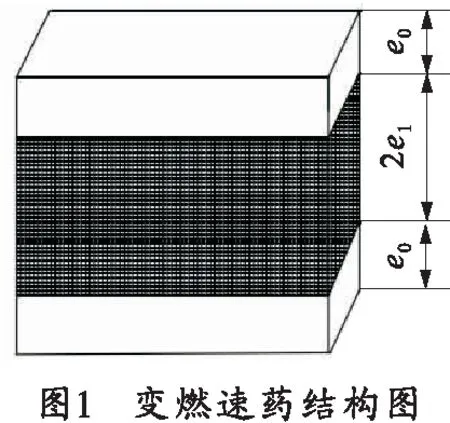
1.2 带状变燃速发射药的已燃质量分数
根据上述的条件,带状变燃速发射药燃烧分为两个阶段,因此带状变燃速发射药的已燃质量分数ψ也应该对应分为两个阶段。
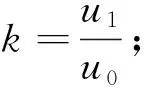
1.2.1 第1阶段已燃质量分数
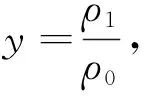
(1)
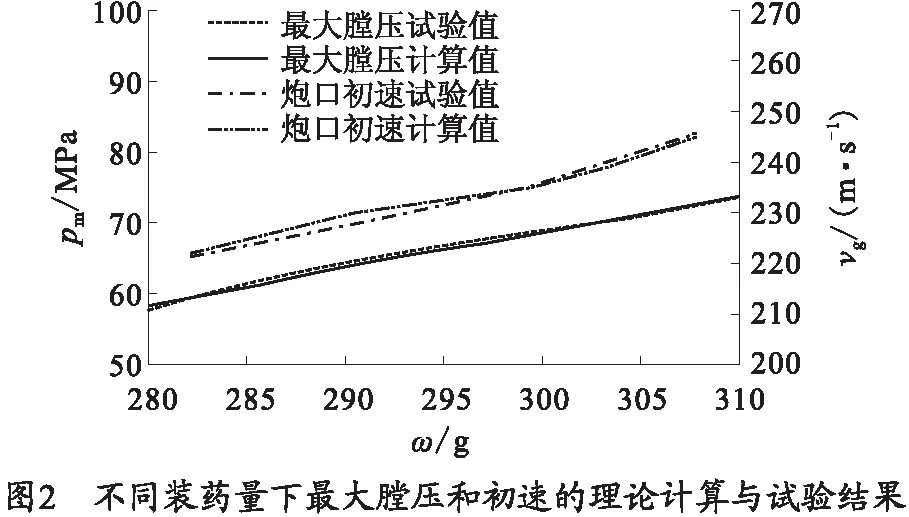
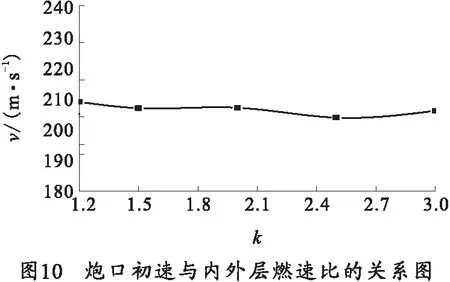
ψ|z (2) 1.2.2 第2阶段已燃质量分数 带状变燃速发射药燃烧第2阶段为外层发射药燃烧结束,内层发射药独立燃烧。外层发射药刚燃烧结束时e=e1,b=b1-ke0,c=c1-ke0,内层发射药独立燃烧,此时e (3) ψ|z>z0=1-{(1-z)(β-kδ+δ-z)· (4) 将带状变燃速发射药用于无后坐力炮,除了经典内弹道假设外,还需要增加如下假设: 1) 火药燃烧速度与压力的关系呈正比,即 2) 火药燃烧时,满足带状变燃速药燃烧假设。 3) 采用绝热指数n,修正因热散失而损失的火药气体能量。 4) 射击过程中未完全燃烧的火药气体只从尾喷管处流出。 上述条件是根据无后坐力炮的特点作出的合理假设,以达到简化无后坐力炮内弹道模型的目的。基于该炮的装药特点,结合经典内弹道理论[13-14],建立如下变燃速药无后坐力炮的内弹道模型。 1)燃烧速度方程: (5) 式中,p为膛内平均压力。 2) 几何燃烧定律方程: (6) 式中, 3) 弹丸运动方程: (7) 式中:v为弹丸速度;t为时间;S为弹丸截面积;F为挤进时期阻力;φ为次要功系数;m为弹丸质量。 4)弹丸行程方程: (8) 式中,l为弹丸行程。 5)气体流量方程: (9) 6) 能量平衡方程: (10) 式中,θ=K-1,K为火药气体的比热比。 7)膛内平均压力: (11) (12) 式中:l0为药室容积缩径长;Δ为装填密度;ρp为火药密度;γ为余容。 依据带状变燃速药无后坐炮内弹道的数学模型,运用 MATLAB软件[15]对该模型进行求解,将求解结果与基于带状变燃速药的无后坐炮开展内弹道性能试验的结果进行对比。理论结果与试验结果表明,建立的数学模型能正确反映基于带状变燃速药无后坐炮的内弹道规律。 当弹丸质量一定时,不同装药量工况下的无后坐力炮最大膛压和初速的理论计算结果与试验结果如图2所示。 从图2中可以看出,数值计算的最大膛压和炮口初速与试验得出的最大膛压和炮口初速有较高的吻合度。最大膛压pm的最大相对误差为2.1%,炮口初速vg的最大相对误差为1.7%.可以得出基于变燃速药的内弹道模型合理,计算结果可以为工程作参考。 火药燃烧规律是内弹道过程中的决定性因素。变燃速火药参数的变化影响火药燃烧规律,从而影响内弹道过程。笔者分析外层厚度与药片弧厚之比δ、内外层药密度比y和内外层燃速比k对内弹道的影响。 在装药量320 g,弹丸质量3 kg,变燃速速药内外层燃速比为2,内外层药密度比为1.5情况下,外层厚度与药片弧厚之比δ分别为0.1,0.3,0.5,0.7时,最大膛压p、炮口初速v和不平衡冲量I的计算结果如图3~5所示。 从图3~5可以看出,不同外层厚度与药片弧厚之比的情况下,不平衡冲量随着δ的增大而减小,变化量相对较小;最大膛压随着δ的增大,先增大后减小;炮口速度随着δ的增大,也有先增大后减小的趋势。 在装药量320 g,弹丸质量3 kg,变燃速速药内外层燃速比为2,外层厚度与药片弧厚之比为0.3情况下,内外层药密度之比y分别为1.1,1.3,1.5和1.6时,最大膛压p、炮口初速v和不平衡冲量I的计算结果如图6~8所示。 从图6~8可以看出,内外层密度比y的变化对不平衡冲量的影响小;最大膛压随着内外层密度比y的增大而增大;内外层密度比y的变化对炮口初速的影响小。因此,降低变燃速药内外层密度比,能减小最大膛压。 在装药量320 g,弹丸质量3 kg,内外层药密度比为1.5,外层厚度与药片弧厚之比为0.3情况下,内外层燃速比k分别为1.2,1.5,2.0,2.5和3.0时,最大膛压p、炮口初速v和不平衡冲量I的计算结果如图9~11所示。 从图9~11可以看出,不平衡冲量几乎不随内外层燃速比改变而改变;最大膛压随着内外层燃速比的增大几乎呈线性减小;炮口初速也随内外层燃速比的增大而缓慢减小。因此,适当增加内外层燃速比,能有效减低膛压的最大值,而几乎不降低炮口初速。 笔者建立了基于变燃速药的内弹道计算模型,而且通过试验证明将变燃速药运用到无后坐力炮中是可行的,同时证明建立的基于变燃速的无后坐力炮内弹道模型是合理的,得出下列结论: 1)随着外层厚度与药片弧厚之比δ的增大,最大膛压和炮口初速先增大后减小,不平衡冲量变化不大。因此,为了减少膛压和不降低初速,外层厚度与药片弧厚之比δ取较小值。 2)随着内外层药密度之比y的增大,最大膛压增大,炮口初速和不平衡冲量变化不大。因此为了减少膛压和不降低初速,内外层密度之比y不能过大。 3)随着变燃速药内外层燃速比k的增大,最大膛压几乎呈线性减小,不平衡冲量几乎不变化,炮口初速缓慢减少。因此,为了减少膛压和不降低炮口初速,变燃速药内外层燃速比k应适当取较大值。 研究结果可为无后坐炮内弹道结构设计及对应的带状变燃速发射药参数确定提供参考。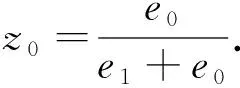
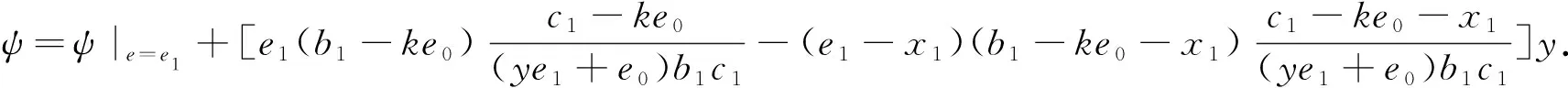
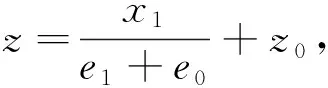

2 内弹道模型

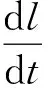
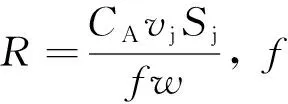
3 数值仿真计算结果及其分析
4 变燃速药对内弹道影响研究
4.1 外层厚度与药片弧厚之比δ对内弹道的影响

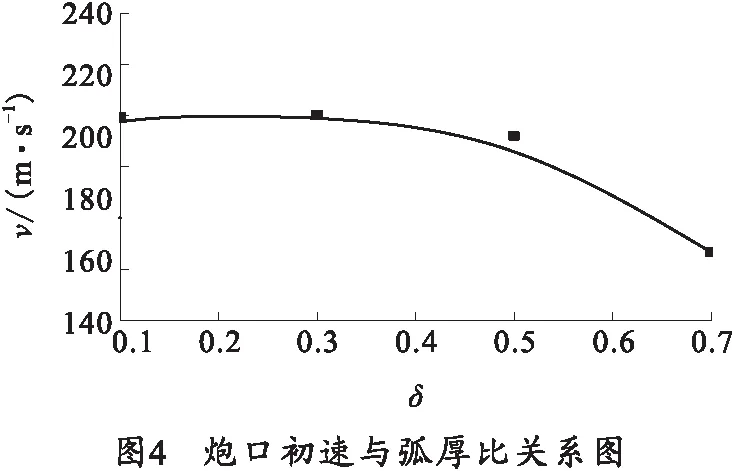
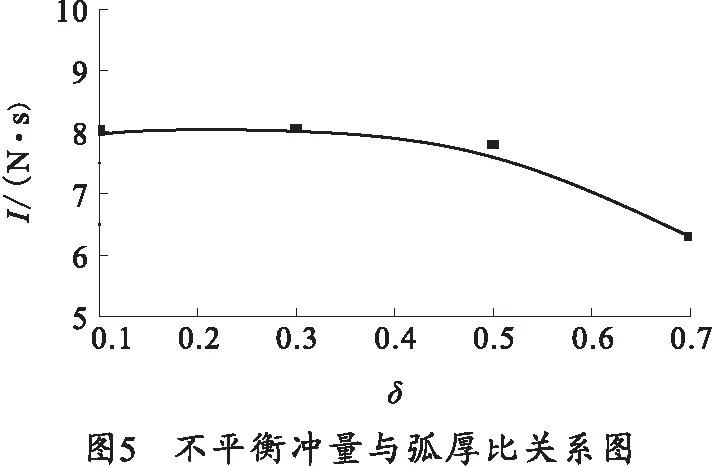
4.2 内外层药密度之y比对内弹道的影响


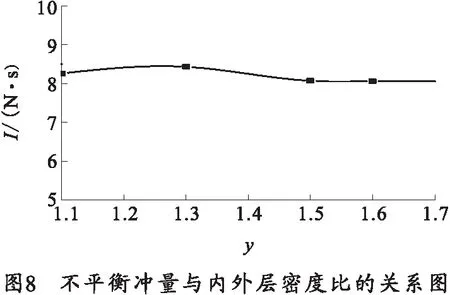
4.3 内外层燃速比k对内弹道的影响


5 结论
