膨胀波火炮扩张喷管减后坐数值模拟

赵秀和，郭张霞，周 军，李 闯，罗 鹏

(中北大学 机电工程学院，山西 太原 030051)

常规闭膛火炮射击时，身管内膛火药燃气燃烧产生的压力一方面作用于弹丸，推动弹丸加速向前运动，使其达到所需的炮口动能；另一方面，火药燃气作用于身管内膛，产生一个沿身管轴线向后的作用力，即炮膛合力，使炮身等构件向后运动[1]，对其后坐部分稳定性造成影响，基于气体动力学原理和拉瓦尔喷管理论提出的膨胀波火炮发射技术是减小火炮后坐的有效途径[2]。膨胀波火炮依靠作用在扩张喷管上沿身管轴线向前的力，可以在保证初速基本不变的前提下大幅减小后坐力，进而为减轻身管质量，简化反后坐装置等提供了可能[3]；而且一部分气体后喷还可以达到降低身管温度，提高身管寿命，清洁药室，减小炮口焰及炮口冲击波的作用[4]。

笔者采用动网格技术以及耦合膨胀波火炮内弹道的方法获取后喷流场的流动状态，得到扩张喷管轴线方向的受力，并进一步计算得到膨胀波火炮炮膛合力，将其与采用膛内平均压力经典内弹道模型计算得到的炮膛合力进行比较，得到膨胀波火炮在减轻后坐冲量方面的贡献。

1 数学模型

1.1 内弹道方程

依照膨胀波火炮的工作原理，考虑惯性炮闩的运动过程，结合经典内弹道的数学模型，可得到膨胀波火炮内弹道方程[5]：

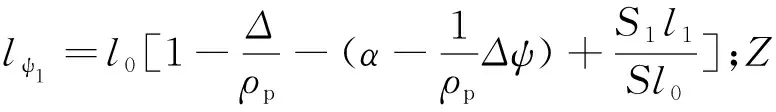
1.2 冲量方程

将经典内弹道求得的膛内空间平均压力代入式(2)可求得闭膛火炮炮膛合力[1]:

(2)

式中：φ1为仅考虑弹丸旋转和摩擦两种次要功的计算系数；b为后效期时间常数；tg为弹丸出炮口时间；tk为后效期结束时间。

对其在时间上进行积分可得其冲量IC为

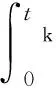
(3)

膨胀波火炮在后喷装置打开之前与常规闭膛火炮的发射过程是一致的[6]，其主要区别在于惯性炮尾打开后膛内气体向后喷出，膛压突降，所以可取膨胀波火炮开闩之前的炮膛合力与闭膛火炮相同[7]，记为F1，其冲量I1为

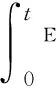
(4)

将仿真得到的惯性炮尾上的受力记为F2，其冲量I2为

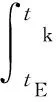
(5)

将仿真得到的喷管上的受力记为F3，其冲量I3为

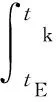
(6)

所以膨胀波火炮的炮膛合力FptR为

FptR=F1+F2+F3,

(7)

其冲量IR为

IR=I1+I2+I3.

(8)

2 仿真模型

2.1 计算模型

以35 mm惯性炮闩式膨胀波火炮为研究对象，以惯性炮闩前断面运动至喷口打开截面的时间为节点开始仿真，闩体随后喷气体向后运动，该模型经简化后可视为轴对称模型，为提高FLUENT运行效率，取其二维模型的1/2进行仿真[8]。其中，口径35 mm，药室长140 mm，药室直径55 mm，惯性炮闩最大后坐行程长0.1 m，喷管前端直径35 mm，喷管后端直径144 mm，喷管长度305 mm，将身管前端中心处设置为坐标原点，沿身管轴线向后为x轴正方向，垂直于x轴竖直向上为y轴正方向，外部计算域x方向取[0 m,6.5 m]，y方向取[0 m,3.5 m].具体计算模型如图1所示。

2.2 网格划分及边界条件设置

划分网格时，考虑到计算机求解速度，对网格的关键求解部分进行局部加密，以保证求解结果尽可能准确，对结果影响较小的部分，网格稀疏一些，具体网格模型如图2所示。

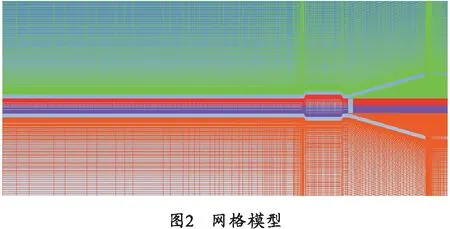
火炮后喷流场属于高速可压缩仿真，选用隐式密度基进行求解。模型选用近壁面函数模型，分别定义对称轴(Symmetry)、压力出口(Pressure-outlet)、壁面(Wall)边界条件及运动边界[9]。如图3所示。

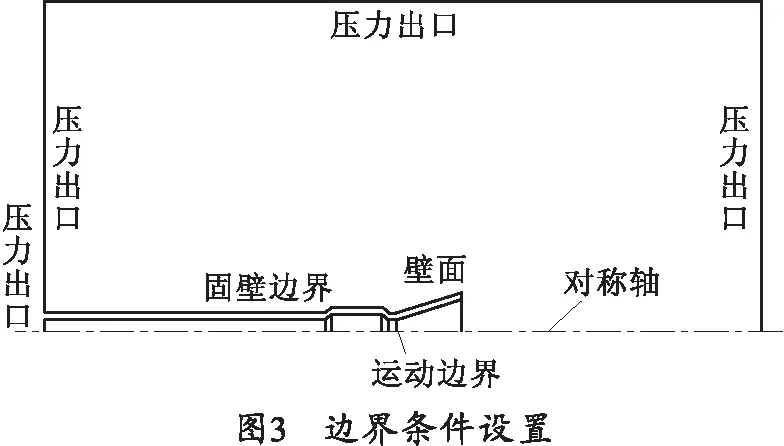
本例中还需要用到动网格技术模拟闩体的运动。动网格首先要指定边界的运动形式，以及参与运动的区域，分别定义变形区域(Deforing)、静止区域(Stationary)、刚体运动(Rigid body)[10]。其次，要指定网格更新的方式，本例中采用四边形网格，故使用层铺法设置动网格，层铺法动网格可以随着边界的移动，单元层逐渐生成或消失，其变形范围无限制，无需显式地指定变形区域内部网格节点的运动，只需给定运动区域的运动规律即可，通过profile文件赋予运动区域一定的平动速度。边界条件定义完成后，利用FLUENT自带的UDF(User Define Function)对计算域压力、温度、速度进行初始化，考虑到火药燃气扩散速度较快，为保证网格能够及时得到更新，取计算步长为5 μs，并设置计算结果每100步自动保存一次。

3 仿真结果及分析

用MATLAB对炮膛合力求解公式进行编程，将由经典内弹道求得的膛内空间平均压力代入得到闭膛火炮炮膛合力，如图4所示。

由图4可得出闭膛火炮炮膛合力冲量为

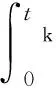
取同等发射条件下的闭膛火炮，选择其在后喷装置打开之前的炮膛合力，作为膨胀波火炮开闩前的炮膛合力，计为F1，其曲线图如图5所示。

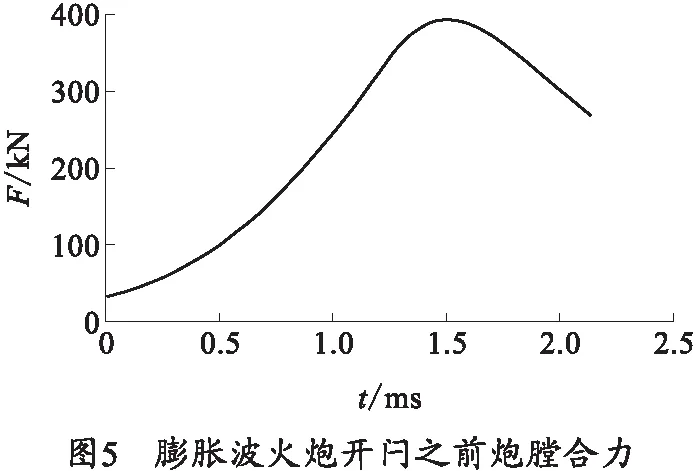
由图5可得出膨胀波火炮开闩之前炮膛合力冲量为

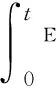
将仿真得到的惯性炮闩上的受力计为F2，其曲线图如图6所示。

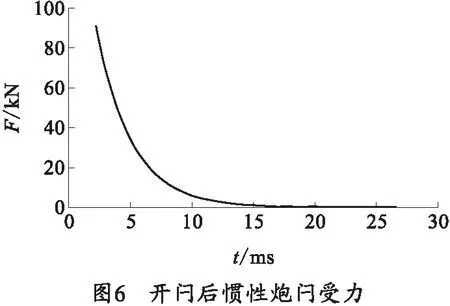
由图6可得出其冲量为

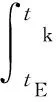
将仿真得到的喷管上的受力计为F3，其曲线图如图7所示。

由图7可得出其冲量为

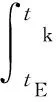
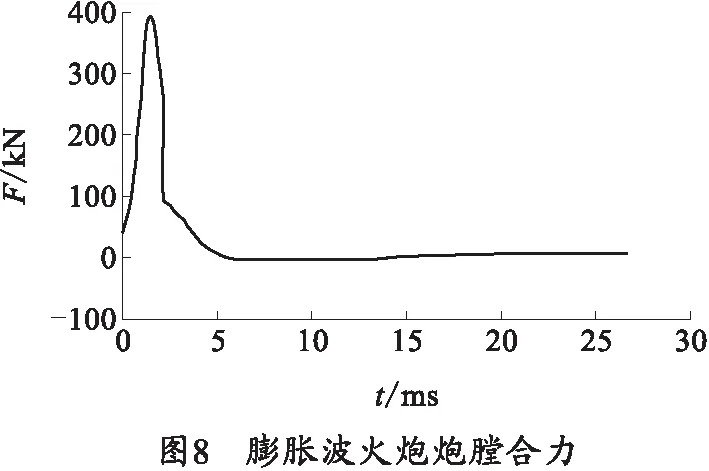
将膨胀波火炮开闩前的炮膛合力、开闩后惯性炮闩受力和喷管受力求和，即可得到膨胀波火炮的炮膛合力曲线图，如图8所示。

由图8可得到其冲量为

IR=I1+I2+I3=524 N·s.

闭膛火炮与膨胀波火炮炮膛合力对比图如图9所示。可以明显看出，开闩后，膨胀波火炮炮膛合力出现突降，且减小较快。

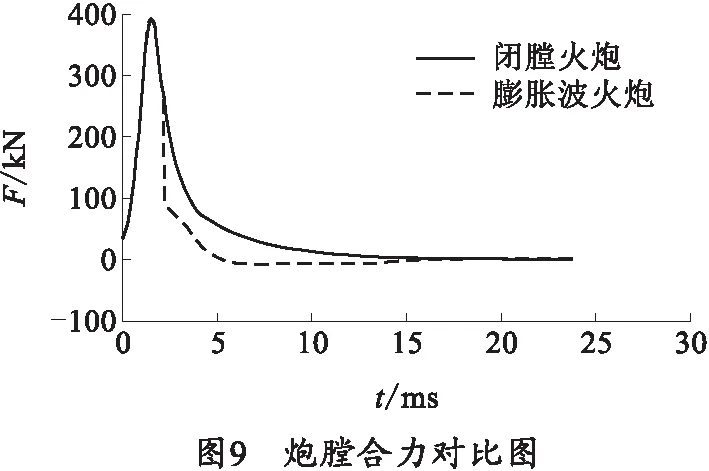
综上所述，闭膛火炮炮膛合力冲量为1 016 N·S，膨胀波火炮炮膛合力冲量为524 N·S.同等发射情况下，膨胀波火炮炮膛合力冲量减少48.4%.

4 结束语

笔者基于二维非定常Euler方程并结合Roe一阶迎风格式，同时采用动态铺层的结构化网格模拟发射过程中惯性炮闩与身管的相对运动。通过FLUENT仿真得到膨胀波火炮发射过程中惯性炮闩及扩张喷管的受力，进而求得膨胀波火炮的炮膛合力与其冲量，并与同等发射条件下闭膛火炮炮膛合力冲量进行比较，结果表明，与传统闭膛火炮相比，在初速基本保持不变的情况下，膨胀波火炮发射过程中炮膛合力冲量减少达48.4%.