组合故障诊断技术在自动装弹机故障诊断中的研究
2020-11-16王国辉马啸飞李向荣吴晓颖
王国辉,马啸飞,李向荣,吴晓颖
(陆军装甲兵学院 兵器与控制系,北京 100072)
新形势下的军事任务和现代战争的特点对主战坦克的射速有了越来越高的要求,自动装弹机的作用也越来越突出。自动装弹机作为主战坦克武器系统中的重要组成部分,是武器系统的核心部件之一[1]。它是一个具有多重控制环节、多种执行机构及众多零部件的复杂机电一体化系统,对于全车的战技指标均具有重大影响。
由于自动装弹机控制环节多,逻辑关系复杂[2],自动装弹机发生故障的概率较高。部队多年使用情况反馈显示,自动装弹机系统结构比较复杂,部队干部战士对此系统没有足够的了解,难以在发生故障时及时进行故障诊断和排除工作。
关于故障树在故障诊断中的研究与应用,现已有不少成果:笔者等[3-4]建立了自动装弹机的故障树,且结合模糊故障树理论对自动装弹机故障诊断方法进行研究,并探索其相应的算法;李俊堂等[5]采用故障树分析法对舰船自动控制系统的各级故障事件进行定性、定量分析,可快速准确地锁定故障发生位置。
针对上述情况,笔者将故障树和确定性理论进行组合,且将此方法应用于主战坦克自动装弹机故障诊断。同时,改变此方法中通过专家评价来设置静态强度的做法,提出基于云模型的静态强度初始化方法。
1 确定性理论
确定性理论是由美国斯坦福大学E.H.Shortliffee等提出的一种不确定性推理模型,该模型用可信度来描述规则的强度,并给出相应的更新算法[6-7]。
该理论主要有以下要素:CF[h,e]为规则的静态强度,取值范围为(-1,1),由专家给出(改进后由云模型得到);MB[h,e]为因证据而对假设的信任增长度;MD[h,e]为因证据而对假设的不信任增长度;CF[e,e′]为假设在当前观察下,e的可信度,取值范围为(0,1),由故障诊断者观测给出[7]。具体定义如下:
给定证据e,假设h成立的可信度CF[h,e]定义为
CF[h,e]=MB[h,e]-MD[h,e].
MB[h,e]表示因证据e的出现,使假设h为真的信任增长度,定义为
MB[h,e]=
MD[h,e]表示因证据e的出现,使假设h为真的不信任增长度,定义为
MD[h,e]=
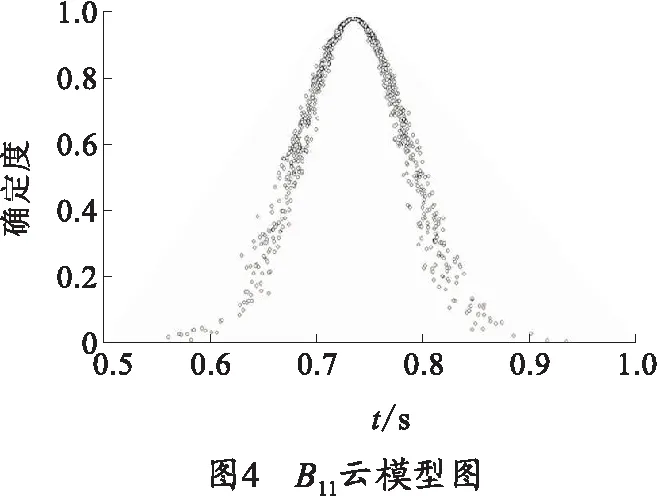
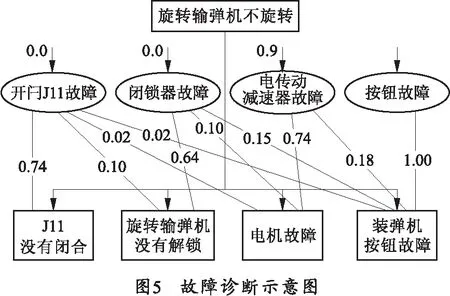
事实上,证据e不可能使P(h|e)>P(h)和P(h|e) 下面给出不确定性更新算法。 1)条件的合取 MB[e1∧e2,e]=min{MB[e1,e],MB[e2,e]}, (1) MD[e1∧e2,e]=max{MD[e1,e],MD[e2,e]}. (2) 由式(1)、(2)可推知: CF[e1∧e2,e]=min{CF[e1,e],CF[e2,e]}. (3) 当证据是多条证据的“和”时,使用式(3). 2)条件的析取 MB[e1∨e2,e]=max{MB[e1,e],MB[e2,e]}, (4) MD[e1∨e2,e]=min{MD[e1,e],MD[e2,e]}. (5) 3)规则的合取 MB[h,e1∧e2]=MB[h,e1]+MB[h,e2]× (1-MB[h,e1]), (6) MD[h,e1∧e2]=MD[h,e1]+MD[h,e2]× (1-MD[h,e1]). (7) 4)由规则的可信度和前提的可信度来计算结论的可信度: MB′[h,e′]=MB[h,e]×max{0,CF[e,e′]}, (8) MD′[h,e′]=MD[h,e]×max{0,CF[e,e′]}. (9) 由此式(8)、(9)推出: CF′[h,e]=CF[h,e]×max{0,CF[e,e′]}. (10) 在规则IFeTHENh(x)被使用时,当e肯定存在时,h以x的可信度为真。当e不确定时,结论h可信度不仅取决于h的静态强度CF[h,e]的值x,也取决于在当前观察下e的可信度CF[e,e′][8].在当前观察下h为真的可信度称作动态强度,用CF′[h,e]表示,可由式(10)算出。 故障是系统不能执行规定功能的状态。故障树是采用树形结构表示故障表征与故障原因之间因果关系的一种推理方法。将故障树应用到自动装弹机故障诊断过程中,具体为:依据故障结构,可将自动装弹机的故障分成多个一级故障,而每一个一级故障又可以分成多个二级故障或者三级故障,以此类推直到故障排除。这样,就可以采用故障树的数据结构来完成对自动装弹机故障知识的表示。在构造故障树时,应将故障知识区分为故障和故障现象。故障是装备发生故障的原因,故障现象是维修人员能够直接观察到或者测量得到的信息,可直接或间接推导出故障原因。故障树顶层对应要诊断的设备,上层父故障则是下层子故障的概括,下层子故障是上层父故障的特例,由此直至具体的故障。 为了适应组合推理的方法,对于故障树做出相应的改造,即:原有的“或”节点不变,将“与”节点转换成“或”节点,如图1所示。由图1(a)故障树可知: A=B×C×D=B×(E+F)×D=BED+BFD, 故,图1(a)的故障树可转换为图1(b). 通过这样的转换,故障树就变为以分系统为根节点的或门加权故障树,每个树节点代表一个故障,节点上的子节点代表上一级故障的子故障。而每个子故障又有很多个故障现象,通过相关的故障现象,即可达成推理的条件,对故障进行推理[9]。示意图如图2所示。 由图2可知,故障树涉及到两类因子,一类是CF[h,e],表示故障现象对子故障的影响程度,称为静态强度(也称影响因子);另一类是CF[e,e′],表示观测因子,由维修人员给出,其取值范围为(0,1),表示人为观测到现象发生的程度。 组合模型即确定性理论与故障树组合的推理模型,其示意图如图3所示。图3中的父故障节点包括3个子故障节点,分别为子故障A、B、C.故障1、2、3、4是在父故障发生的前提下观测到的故障现象,现象与故障的连线上所带数字表示现象对故障的影响因子。 以故障现象1为例,其所对应的规则表示为产生式形式即: IF故障现象1发生THEN子故障A发生(0.2); IF故障现象1发生THEN子故障B发生(0.4); IF 故障现象1发生THEN子故障C发生(0.3). 现象上方箭头所带的数字表示观测因子,由维修人员提供,取值范围为(0,1),表示故障现象发生的程度。根据上述数据,即可进行计算,步骤如下: 1)由于有4个可能的现象,但每次只能就1个现象进行询问,因此依据现象对子故障影响个数进行排序。就图3而言,现象1影响了3个子故障,现象4影响1个子故障,所以先对现象1进行询问,最后对现象4进行询问。 2)对于故障现象1,维修人员给出的观测因子为0.9,那么根据式(10)可分别算出3个子故障的动态强度。对图3故障现象1而言,对应子故障的动态强度分别为:0.18、0.36、0.27. 3)将各动态强度与阈值(此值由维修人员设置)进行比较,看是否大于阈值,若没有则询问下一个故障现象,如果大于阈值的子故障动态强度多于1个也询问下一个故障现象。当有且只有1个子故障动态强度大于阈值为止。否则重新设定阈值。 4)如果到最后一个故障现象询问完毕后,仍存在大于1个的子故障动态强度高于阈值,那么就应该适当提高阈值。如果所有的子故障动态强度都小于阈值,那么就适当减小阈值。并从第2步重新开始,以此方法不断循环,直至叶节点,即为所求的故障原因。 观测因子的给定方法:若肯定故障现象的存在,则观察因子给予0.9;若肯定故障现象的不存在,则观察因子给予0.0;若无法肯定故障现象是否存在,可能发生时观察因子给予0.7,不可能发生时观察因子给予0.3. 阈值的给定方法:首先根据现象对故障的静态强度制定,即对应子故障最多现象的最大的静态强度的0.9倍。当需要调整阈值时,根据观察因子的大小结合实际情况进行调整。 由上述可知静待强度是组合推理的一个重要参数,它的高低意味着故障现象对子故障的影响的强弱。以往静态强度是根据专家评价来设置,现采用云模型的方法进行设置。 云模型由李德毅院士于1995年提出,是一种实现定性概念与定量数值表示方式的双向认知模型[10]。它的数字特征可由3个变量来概括:云滴分布的数学期望Ex、度量定性概念不确定性的熵En、反应定性概念接受程度的超熵He. 在明确故障现象对子故障的静态强度时,使用云模型来替代传统方法更能反映静态强度的不确定性。这样做的好处是可以降低以往单个专家直接给出静态强度做法的误差,增加静态强度的可信度。其具体步骤如下。 为了更好地确定故障现象对子故障的静态强度,首先确定现象对故障的评语集,尔后由m名专家组成的专家群E={Ei|i=1,2,…,m}提出现象对子故障的影响等级评语集R={Rj|j=1,2,…,n}.专家Ei在论域[0,1]上给出rj的区间数为cij=[aij,bij],0≤a≤b≤1,全部专家的意见合成为矩阵C=(cij)m×t.接着让每个专家给定每个评语等级所对应区间的数值,之后将这些数值合成并求取平均数,得到云化区间数cj: (11) 文献[11]确定云模型3个数字特征的方法是在2倍熵原则的基础上对指标近似法进行改进所得到的。用正态云模型描述当j=1,2,…,t-1时对应的评语: (12) 用半云模型来描述当j=1或j=t时对应的评语: (13) 为了保证云模型的准确性,采用文献[12]提出的一种通过2倍熵原则的方法,计算专家Ei对评语j的评语区间的数值与评语j确定区间数值的差异度ηj(j=1,2,…,t),来确定超熵的值。ηj的计算公式为 (14) j=1,t和j=2,3,…,t-1的区间数所映射云模型的超熵的计算公式为 (15) 专家群对某个静态强度p进行评判后产生了m个评判意见,为了便于分析,用一个云模型来表示,其期望为Exp,熵为Enp.通过式(6)、(7)可以计算出云模型的期望与熵: (16) (17) He值一般为0.05En~0.15En,在2倍熵原则下,Hep取值为 Hep=0.1Enp. (18) 根据上述所求取的评语描述云,专家群对静态强度p的评价云为Cp=(Exp,Enp,Hep).若专家i对静态强度p的评价为Sij,那么可依据下式实现Sij向Exp的转换: Sij→Exp→Exij. (19) 这样,静态强度p的评语确定度Y通过正向云发生器计算得出: Y=exp[-(xp-Exp)2/2(En′)2], (20) 式中:xp为正向云发生器以Exp为期望、Enp为方差生成的正态随机数;En′为以Enp为期望、Hep为方差生成的正态随机数。 现有一台主战坦克自动装弹机发生故障,其故障表现为旋转输弹机不旋转,后经专家检测认为是电机故障造成的。结合上述诊断方法对该故障原因进行推理,以此验证该诊断方法。 采用调查问卷的形式,邀请该领域的6名专家,分别给予评语的区间和故障现象对子故障的影响等级。为了确保专家的意见能够较为完整统一的反映,规定评语集为5个等级:①不影响;②有一点影响;③有一部分影响;④有大部分影响;⑤完全影响。由6名专家分别确定各个评语等级的区间所对应的数值,依式(11)进行计算,得到的评语等级的云化区间,如表1所示。 表1 评语等级的取值区间 由式(14)计算出专家所确定的区间数值与上述区间数值的差异度,如表2所示。 表2 评语等级对应的差异度表 按式(12)、(13)、(15)得出各评语的云化区间的云模型数字特征,如表3所示。 表3 各区间对应的云模型数字特征 根据已知的故障,可能的故障现象有4个,对应的子故障有4个,对应的影响度有B11~B44.由专家给出现象对子故障的影响度的评语等级,则形成的评语矩阵S为 当所有专家都认为某个影响度为①时,则可认为其对应的故障现象对子故障没有影响,在接下来的诊断中不予考虑。 由式(16)~(19)可以得到各个影响度的云模型数字特征,如表4所示。 表4 各影响度对应云模型 根据得到的数字特征,使用Labview软件进行云模型可视化处理,则可得到相应的云图。图4是B11所对应的云图。 利用云发生器进行静态强度的计算,如B11为0.74,之后以此类推,得到所有的静态强度。得到的静态强度在图5中标出。 1)将“旋转输弹机不旋转”作为父故障,可能的故障现象有4个,依据影响子故障的多少将4个故障现象进行排序。设定阈值为0.6. 2)对排序第1的故障现象进行询问,即查看开关J11是否良好,有无故障。经检查,开关J11没有故障,且闭合。故给予第1个故障现象一个较低的观测因子0.0,表示不存在这个现象。 3)对排序第2的故障现象进行询问,即查看旋转输弹机闭锁器是否良好,有无故障。经检查,闭锁器良好没有故障,旋转输弹机解脱闭锁。故给予第2个故障现象一个较低的观测因子0.0,表示不存在这个现象。 4)对排序第3的故障现象进行询问,即查看电传动减速器是否良好,有无故障。经检查,电传动减速器发生故障。故给予第3个故障现象一个较高的观测因子0.9,表示存在这个现象。 5)按照式(10)进行计算,其影响的两个子故障动态强度分别为0.63、0.09,故第1个子故障动态强度超过阈值,可以确定旋转输弹机不旋转的故障原因是电传动减速器的电机故障。 笔者在研究故障树和确定性理论的基础上,将两者结合形成组合推理模型,并应用于主战坦克自动装弹机故障诊断中。通过实例分析显示,该方法用于故障诊断,清晰、便捷,逻辑关系强,引入了观察因子,降低了对使用者专业水平的要求,提高了故障树的实用性,增加了故障诊断的推理效率,对保障主战坦克的作战能力有积极的意义。2 故障树的适应性改造
2.1 故障的表示
2.2 故障树的适应性改造
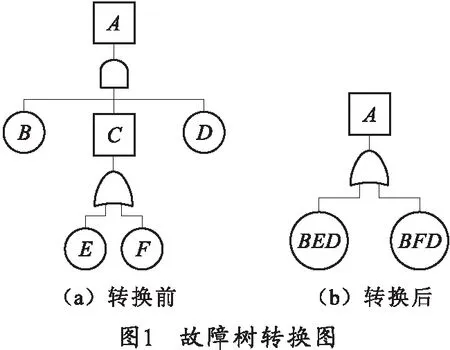
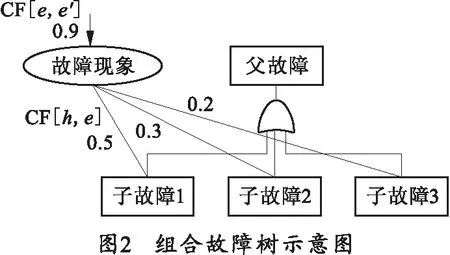
3 组合模型的推理方法
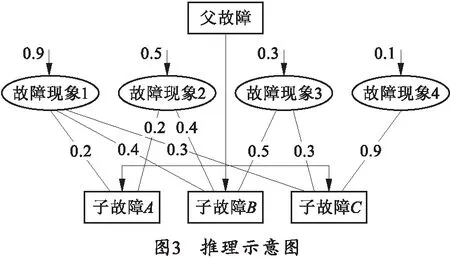
4 基于云模型的静态强度设置
4.1 建立等级评语的云概念
4.2 参数值的云合成
4.3 评语确定度的计算
5 实例验证
5.1静态强度的初始化
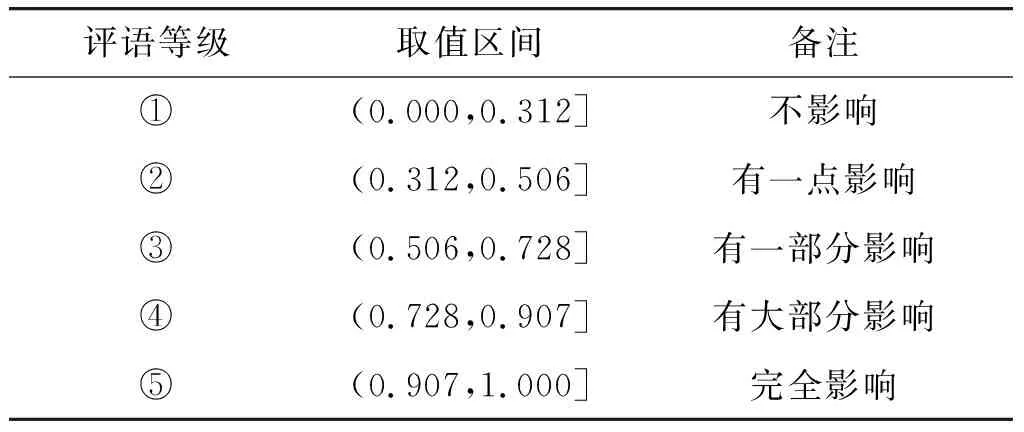




5.2 故障诊断具体步骤
6 结束语
