考虑横向转运的线状需求物流节点选址研究

周建勤，李 敏，隋雨函

(北京交通大学 经济管理学院，北京 100044)

截至2019年4月，全国铁路网规模达13.1万km。到2025年，铁路网规模将达到17.5万km，尚有4万多km铁路待建设。铁路线路的建设需要大量的物资，且拟建线路上连续各点都有需求，为线状需求。为满足线路建设的物资需求，通常沿拟建线路布局一定数量的物流节点，接收并储存从工厂运来的物资，并根据实际需要将其运输至需求路段。此外，不确定因素常发生于需求路段中，导致需求路段所需物资随时间变化且具有随机性，从而使各物流节点处的库存失衡。而引入横向转运将有效解决此问题。因此，探讨物流节点的选址问题，对末端的物流成本控制具有重要意义，进而对铁路线路建设有一定影响。

大多数设施选址文献的研究都是基于离散需求，也有一些学者研究线状需求下的选址问题。Alonso[1]以沙滩线沿岸连续分布的冰淇淋需求为研究对象，确定冰淇淋店的选址。Rosenhead等[2]通过决策沿线设施的位置，来最小化沿线分布的客户到最近设施的期望距离。周建勤[3]使用需求密度函数表示拟建交通线路的物资需求密度，并用线积分描述线状连续的物资需求。Gastner[4]以居住地点到最近设施的平均距离最小化为目标，研究了线路上连续需求的物流节点选址及需求分配问题。Erdemir等[5]基于离散需求和线状需求，建立选址模型，并运用算例阐明了线状需求下选址模型的优越性。以上学者研究了线状需求下的设施选址问题，尚未将库存纳入考虑。

当需求不确定时，一些学者探讨了联合选址–库存问题。Shen等[6]提出了联合选址–库存模型同时决策库存和选址，研究了单供应商和多零售商的联合选址–库存问题。Daskin等[7]提出了以库存成本和运输成本之和为联合选址–库存模型的目标函数。原丕业等[8]建立了非线性整数规划的选址–库存模型。周愉峰等[9]研究了国家血液战略储备库的选址–库存模型。王林等[10]构建了联合补货–选址库存协同优化模型。若开展库存控制与设施选址联合优化，能降低需求不确定性带来的影响。

物流节点间的横向转运策略常被引入到选址–库存联合优化中。Tagaras等[11]将横向转运引入联合选址–库存问题，考虑了订货提前期和转运时间的两设施横向转运机制，论证了设施选址分配决策受横向转运影响。Shen等[6]、Shu等[12]、Snyder等[13]针对零售商之间的横向转运问题，以优化选址和库存为目标，建立了非线性整数规划模型。Shen等[6]研究了考虑横向转运的选址模型，将该模型转化为集分割问题，通过列生成算法求解。Shu等[12]进一步研究和改进了Shen等[6]的算法。Snyder等[13]提出了基于拉格朗日松弛的精确算法，通过低阶多项式求解模型。上述学者都是研究了横向转运的选址–库存联合优化问题，然而他们针对的是离散需求，目前还没有将横向转运考虑进线状需求下的设施选址的文献。

本文针对需求沿线路连续分布的情形，考虑了物流节点之间横向转运的策略，构建了需求随时间不确定下的选址–库存模型，在分析模型性质的基础上，设计线搜索算法求解，并结合算例验证模型的可行性和有效性。

1 问题描述与模型构建

1.1 问题描述

大多数拟建铁路线路空间跨度大，经过丘陵、平原和湖泊等不同的地理环境时，需要架设桥梁、隧道等。各段线路建设所需的物资数量各不相同。确定线路建设物资需求密度变化的关键节点，将拟建线路划分为多个子区段，各子区段内物资需求密度在空间上均匀分布。同时，在不同时间阶段内各子区段的物资需求密度随机变化。拟选址的物流节点分布在拟建线路上，其供应的物资沿拟建线路运输至线路上的各处需求点。

不失一般性，本文将拟建线路拓扑为一条直线段，2个物流节点分别选址在该直线段上，且物流节点1负责满足左端点至需求分界点的物资需求，物流节点2负责满足需求分界点至右端点的物资需求。在物流节点处储存物资，并将物资运输至需求点，当物流节点的库存水平不均衡时，物流节点之间采用横向转运的方式调配物资。模型以运营总成本最小化为目标，决策物流节点和需求分界点的位置。

为了便于分析问题，现作出如下假设：

1) 拟建线路各子区段的物资需求相互独立；

2) 横向转运的物资瞬时到达；

3) 拟建线路中同一子区段内各处的需求密度相同。

1.2 模型构建

1.2.1 符号说明

K为拟建线路子区段的数量；

p0为拟建线路的起始位置；

pk为拟建线路第k子区段的右端点，k=1,2,···,K；

lk为第k子区段的长度；

µk为第k子区段需求密度的均值;

δk为第k子区段需求密度的标准差;

j=1,2为物流节点的编号；

xj为第j个物流节点的位置；

d为需求分界点的位置；

f(x)为线路建设期内需求密度的均值；

Sj为 物流节点j的期初库存水平；

Zj为 物流节点j需要满足的线路总需求；

Fj(·) 为物流节点j需要满足的总需求的分布函数；

Qij为物流节点i到 节点j的转运物资数量；

ec为物流节点到拟建线路上各需求点的运输费率；

eh为库存持有费率；

ep为库存短缺费率；

et为横向转运费率；

Gj为物流节点j转运后的净库存；

为转运后，物流节点j处的持有库存；

为转运后，物流节点j处的短缺库存。

1.2.2 建立模型

拟建线路为x轴 上K个首尾相连的子区段，如图1所示。

图1 铁路线路子区段划分图Figure 1 Diagram of railway route division

各子区段内需求沿线路均匀分布，其需求密度均值f(x)为

对于第k子区段，其线路长度为lk，需求密度均值为 µk，标准差为 δk，则在建设周期内第k区段的总需求量服从正态分布

2个物流节点的需求分界点为d，d∈(pn−1,pn)。因而物流节点1的服务范围是[p0,d]，物流节点2的服务范围是[d,pK]，如图2所示。

图2 物流节点服务范围图Figure 2 Diagram of logistics node service scope

物流节点1服务范围的需求均值和方差分别为

同理可得物流节点2服务范围的需求均值 µ˜2和方差

由于需求不确定，物流节点j持有安全库存，其期初库存水平表示为Sj=µj+aδj，a为安全库存系数。如果一个物流节点的库存仍然无法满足其物资需求时，则可以通过另一个物流节点转移库存来满足部分或者全部需求。

根据文献[14]，2个物流节点可能出现的横向转运情况如下

1) 如果S1＞Z1且S2＞Z2，则Q1,2=Q2,1=0；

2) 如果S1≤Z1且S2≤Z2，则Q1,2=Q2,1=0；

3) 如果S1＞Z1且S2＜Z2，则Q1,2=min{S1−Z1,Z2−S2}，Q2,1=0；

4) 如果S1＜Z1且S2＞Z2，则Q1,2=0 ，Q2,1=min{Z1−S1,S2−Z2}。

在单位周期内，物流节点的期初库存满足拟建线路的物资需求后，若2个物流节点均缺货或均持有库存，则无需横向转运；若1个物流节点持有库存，另一节点缺货，则2个物流节点间进行横向转运，直到库存短缺的物流节点需求被满足或持有库存的物流节点库存被消耗完。

物流节点到需求点的末端运输成本由运输量、运输距离和运输费率3者共同决定。物流节点1到线上需求点x的距离表示为 |x1−x|，物流节点2到线上需求点x的距离表示为 |x2−x|。依据文献[15]，核算运输成本时，可以用期望需求量代替实际需求量。

物流节点1、2的末端运输成本之和为

物流节点的库存成本由库存持有成本和库存短缺成本组成。参考文献[16]，以物流节点1需要满足的建设物资总需求Z1为横轴，以物流节点2需要满足的建设物资总需求Z2为纵轴，观察2个物流节点可能出现的库存状态和横向转运情形，如图3。

图3 物流节点可能出现的库存及横向转运情形Figure 3 Possible inventory and transshipment situations at logistics node

图3的区域①中，2个物流节点的期初库存量都大于各自的需求量，故2个物流节点间不发生转运，且各自的期末库存量都为正。图3的区域②中，物流节点1的期初库存量大于其需求量，物流节点2的期初库存量小于其需求量，且2个物流节点的期初库存量之和大于其总需求量，故物流节点1向物流节点2转运以恰好满足物流节点2的需求。转运后，物流节点1的期末库存量仍为正，物流节点2的期末库存量为0。图3的区域③中，物流节点1的期初库存量大于其需求量，物流节点2的期初库存量小于其需求量，且2个物流节点的期初库存量之和小于总需求量，故物流节点1将剩余库存全部转运至物流节点2。转运后，物流节点2的一部分需求得到满足，但仍然缺货。因此，物流节点1的期末库存量为0，物流节点2的期末库存量为负。图3的区域④、区域⑤和区域⑥对应于类似的情形。

横向转运后，物流节点1的期望库存持有数量是图3中区域①和②的面积之和

转运后，物流节点1的期望缺货数量是图3中区域⑤和⑥的面积之和

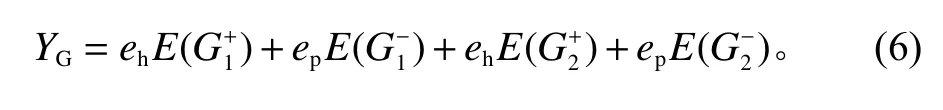
横向转运成本由横向转运距离、转运量和转运费率3者共同决定。物流节点1为物流节点2横向转运的期望横向转运数量，为图3中区域②和③的面积，表示为

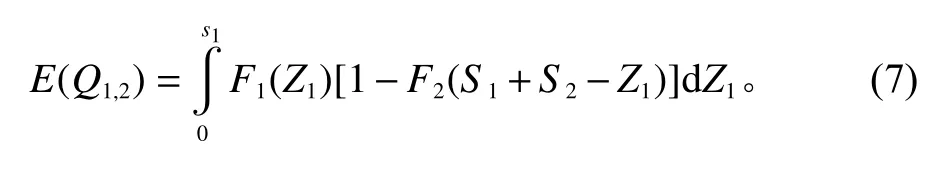
同理可知物流节点2为物流节点1横向转运的期望横向转运数量。那么2个物流节点的横向转运成本可以表示为

选址模型的总成本由末端运输成本、库存成本和横向转运成本组成，从而将考虑横向转运的线状需求物流节点选址模型表示为

在式(9)中，决策变量分别为需求分界点的位置d、物流节点1的位置x1、物流节点2的位置x2，它们都是连续型变量，可以分布在线路的任意位置。

最优选址性质定理在考虑横向转运的线状需求物流节点选址模型中，若1个需求分界点位置d=d(0)已知，则物流节点1最优位置所在子区段n1满足式(10)和式(11)时，的表达式如式(12)所示；物流节点2的最优位置所在子区段n2满足式(13)和式(14)时，的解析式如式(15)所示。

其中，QL表示两个物流节点的平均横向转运量,QL=E(Q1,2)+E(Q2,1)。

2 算法设计

最优选址性质定理指出了2个物流节点最优位置需要满足的条件。本文设计了线搜索算法，求得需求分界点和2个物流节点的最优位置，步骤如下。

步骤1令搜索步长为设定的搜索次数，并令计步器

步骤2根据搜索步长，计算需求分界点的位置并令计步器加1。

步骤3根据式(10)和式(11)计算得到物流节点1最优位置所 在 子 区 段n1[w]，根 据 式(13)和 式(14)计算得到物流节点2的最优位置所在子区段n2[w]。

步骤4将n1[w]代入式(12)中得到物流节点1最优位置x1[w]，将n2[w]代入式(15)中得到物流节点2的最优位置x2[w]。

步骤5由d[w]、x1[w]、x2[w]可得运营总成本Y[w]，返回到步骤1，直到w＜N，停止计算。选择Y[w]值最小的解为最优解。

3 算例分析

拟建铁路线路长度为328 km，在工程建设预算的限制下，在线路上设置2个物流节点以供应线路建设所需物资。

以线路需求密度变化处为关键节点，将该需求线路划分为6个子区段，其长度、需求密度均值以及需求密度标准差如表1所示。

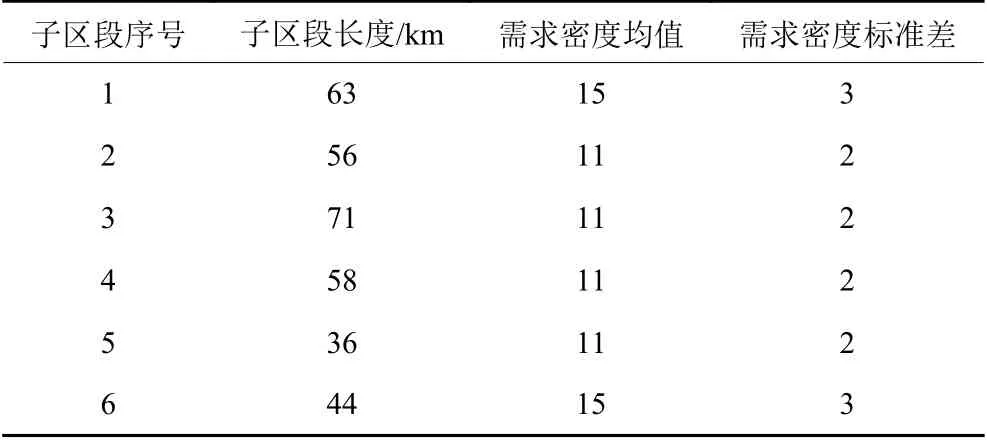
表1 参数表示Table 1 Parameter representation

物流节点满足线路建设物资需求时，末端运输费率ec=4元 /（t·km），库存持有费率eh=400元/t，短缺费率ep=4000元 /t，横向转运费率et=6元/（t·km）。设置安全库存系数a=1。

本文采用Matlab2018b编写代码，求解考虑横向转运的线状需求物流节点选址模型的物流节点最优位置和需求分界点最优位置。当线性搜索次数为200时，得到运营成本随需求分界点的变化曲线，如图4所示。

图4 需求分界点对总成本的影响曲线Figure 4 Cost curve of demand cut-off points

由图4可以看出，无论需求分界点在何处，发生转运后的总成本总是比不发生转运的总成本小，其中，需求分界点在160.72 km处时，发生转运时的总成本最低，为940020元。以上说明需求分界点的位置影响总成本，合理的决策需求分界点可以节省成本。此外，横向转运有助于降低总成本。

由表2可知，在上述分界点处，考虑横向转运时，转运成本增加了26633元，运输成本增加了4437元的，同时，库存成本降低了104856元，总成本降低了73786元。考虑横向转运使库存成本显著下降，降低了31.0%，进而使总成本降低了7.3%。因此，考虑物流节点间的横向转运对成本控制效果显著表2。

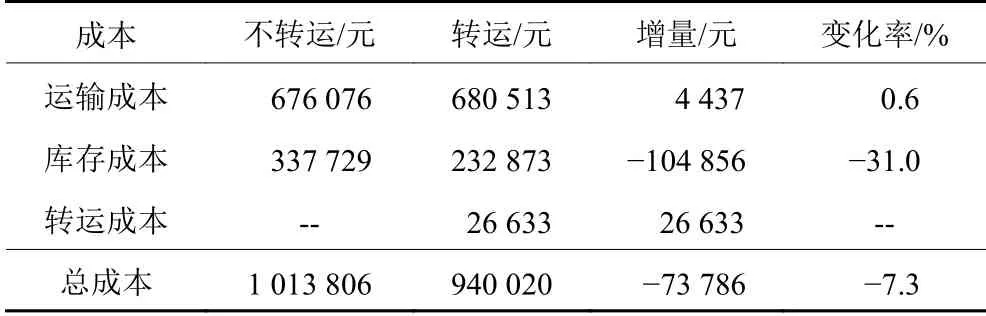
表2 各个成本及其变化率Table 2 Each cost and its rate of change

在考虑横向转运的条件下，不同的物流节点选址对总成本有影响，如图5所示。合理决策物流节点位置，有利于降低运营总成本。

综上，当铁路线路建设物资需求不确定时，物流节点间进行横向转运优于不转运，且物流节点和需求分界点的位置决策都会影响运营总成本。因此，在物流节点选址和需求分配阶段，建议管理者考虑横向转运的影响，以得到更优的物流节点选址和需求分配决策，控制库存成本，进而控制物流总成本。

图5 考虑转运下物流节点位置对总成本的影响曲线Figure 5 Cost curve of logistics node location considering transshipment

4 结束语

本文界定了考虑横向转运的线状需求物流节点选址问题，以最小化物流节点运营总成本为目标，构建了选址−库存模型，确定2个物流节点的最优位置和需求分配。通过分析模型性质，设计线搜索算法来求解物流节点最优位置和需求分界点最优位置。论文还指出物流节点选址受横向转运的影响，结果表明，考虑横向转运可以降低物流节点的库存成本，进而降低总成本。

未来的研究可以从以下方面拓展。1) 可以将需求线路拓展为二维空间形态，并选用其他的距离函数刻画运输距离。2) 本文确定需求分界点的最优位置时，采用的线搜索算法，可能存在误差，具体的算法设计可进行优化。