数列裂项求和的“源”与“流”

天津 高成龙

有一些数列的前n项和可以利用求和公式模型来求解，如等差数列前n项和是关于n的过原点的二次函数，它的求和公式模型为Sn=An2+Bn(A,B为常数，由a1,a2唯一确定).等比数列求和公式模型为Sn=A-Aqn(q为公比，A为常数，由a1唯一确定)，等差数列乘以等比数列的求和公式模型为Sn=A+qn(Bn-A)(q为等比数列的公比，A,B为常数，由a1,a2唯一确定).还有一些重要的数列虽然没有求和公式模型，但是可以通过对通项进行等价变形，利用裂项求和的方法来求解.下面先探究可以利用裂项求和的数列类型.

一、裂项求和的“源”

1.学生在裂项中常见的问题

2.裂项求和的模型

模型1若数列an=f(n+k)-f(n)(k∈N*)，则数列{an}的前n项和为Sn=f(n+k)+…+f(n+2)+f(n+1)-f(1)-f(2)-…-f(k).

3.裂项求和模型的特点

通过模型1可以发现裂项求和的结果是对称的，主要表现在：①前后剩余个数相同，均为k个；②前面k个数的符号与后面k个数的符号相反；③前后剩余的位置相同，即前面是正数第i个和正数第j个，后面则是倒数第i个和倒数第j个.

二、裂项求和的应用

裂项求和是高考数列中常用的方法，近三年高考中出现的频率较高，2017年天津(文)18题、2017年天津(理)18题、2018年天津(理)18题、2018年浙江20题、2019年天津(理)18题、2019年天津(文)18题、2019年浙江20题的数列问题均可以利用裂项方法来求和.下面以三道题为例来探究裂项求和问题.

【例1】(2017·天津卷理·18)已知{an}为等差数列，前n项和为Sn(n∈N*)，{bn}是首项为2的等比数列，且公比大于0，b2+b3=12,b3=a4-2a1，S11=11b4.

(Ⅰ)求{an}和{bn}的通项公式；

(Ⅱ)求数列{a2nb2n-1}的前n项和(n∈N*).

解析：(Ⅰ)an=3n-2；bn=2n.

(Ⅱ)解法1：错位相减法

由(Ⅰ)可得a2n·b2n-1=(6n-2)·22n-1=(3n-1)×4n，令数列{a2nb2n-1}的前n项和为Tn，

Tn=2×4+5×42+8×43+…+(3n-1)·4n，

4Tn=2×42+5×43+8×44+…+(3n-4)·4n+(3n-1)·4n+1，

上述两式相减，

得-3Tn=2×4+3×42+3×43+…+3·4n-(3n-1)·4n+1

=-(3n-2)·4n+1-8.

解法2：裂项法

设cn=(3n-1)·4n，利用模型1，设f(n)=(an+b)·4n，则f(n+1)=(an+a+b)·4n+1，

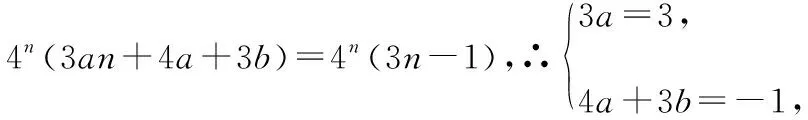
方法点评：比较上述两种方法，错位相减法更接近学生的最近发展区，通俗易懂，但是对学生的计算能力要求比较高.尤其是对于最后的结果进行化简时，学生没有一个明确的目标或形式去靠近，最终结果的化简给求解带来很大的障碍.以该例说明学生运用错位相减法常见的错误有：①两个式子作差时，最后一项的符号忘记改变；②运用等比数列前n项和公式对42+43+…+4n-1+4n求和时把项数当成n项；③对Tn进行化简过程中合并同类项、提取公因式环节出错导致最后形式不对.下面给出一般的等差数列乘以等比数列求和的裂项模型：

模型2设{an}是等差数列，{bn}是公比为q的等比数列，则数列{an·bn}的前n项和可以利用裂项求和求得，且anbn=f(n+1)-f(n)，其中f(n)=(an+b)·qn，a,b可以由a1b1,a2b2唯一确定.

【例2】(2018·天津卷理·18)设{an}是等比数列，公比大于0，其前n项和为Sn(n∈N*)，{bn}是等差数列.已知a1=1，a3=a2+2，a4=b3+b5，a5=b4+2b6.

(Ⅰ)求{an}和{bn}的通项公式；

(Ⅱ)设数列{Sn}的前n项和为Tn(n∈N*)，

(ⅰ)求Tn；

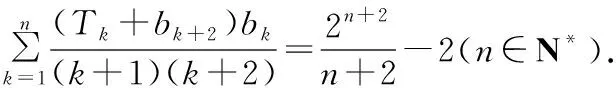
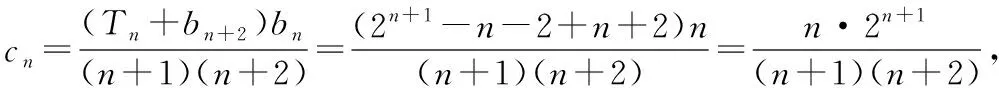
解析：(Ⅰ)an=2n-1，bn=n.(Ⅱ)(ⅰ)Tn=2n+1-n-2;

【例3】(2019·浙江卷·20)设等差数列{an}的前n项和为Sn，a3=4，a4=S3，数列{bn}满足：对每个n∈N*,Sn+bn,Sn+1+bn,Sn+2+bn成等比数列.

(Ⅰ)求数列{an},{bn}的通项公式；

分析：(Ⅱ)不能直接求出数列{cn}的前n项和，但是通过放缩可以将{cn}转化为容易求和的裂项形式.

解析：(Ⅰ)an=2(n-1)，bn=n(n+1)；(详细过程略)

点评：裂项相消法可以直接求数列的前n项和，但是有一些数列本身无法求和或者求和较为麻烦，可以利用不等式转化为裂项相消求数列和，再加以解决，常见于数列的放缩问题.

三、裂项求和的“流”

1.问题的来源

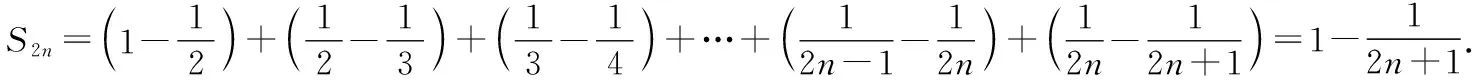
2.问题1再探究

利用加法交换律与结合律对于问题1的S2n进行变形便有：

模型3：若数列an=(-1)n(f(n+k)+f(n))(k∈N*)，则数列{an}的前2n项和为S2n=f(2n+k)+…+f(2n+2)+f(2n+1)-f(1)-f(2)-…-f(k).

我们把上述数列求和的方法叫做并项求和.下面讨论上述数列模型在求和中的应用.

3.数列的并项求和应用

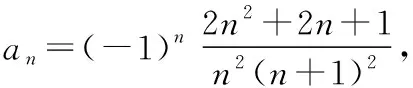
解法1 并项求和

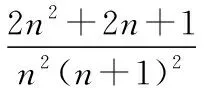
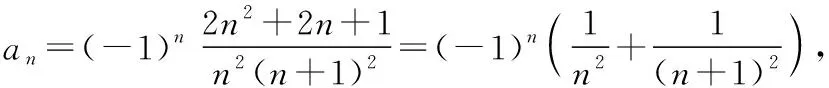
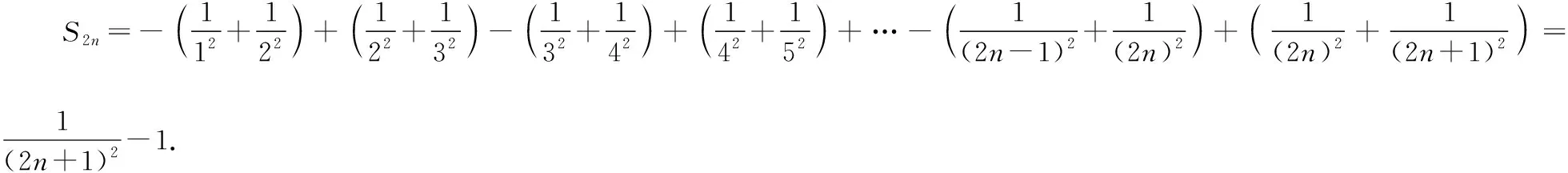
由于数列并项求和是由数列裂项求和衍生出来的，我们回归到并项求和的本质，对数列相邻两项进行结合，便可以运用裂项求和求解例4.

解法2 裂项求和

解析：数列相邻两项结合便有

点评:解法2采用相邻两项结合，将二次转化成一次，将未知数列转化成学生熟悉的数列模型进行求解.

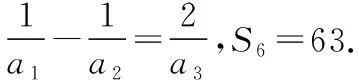
(Ⅰ)求{an}的通项公式；

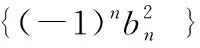
解析：(Ⅰ)an=2n-1；

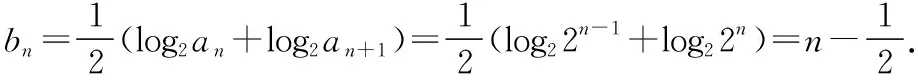
=2n2.

模型4若数列{an}满足an=(-1)n(an2+bn+c)，则{an}的前2n项和为S2n=2an2+(a+b)n.

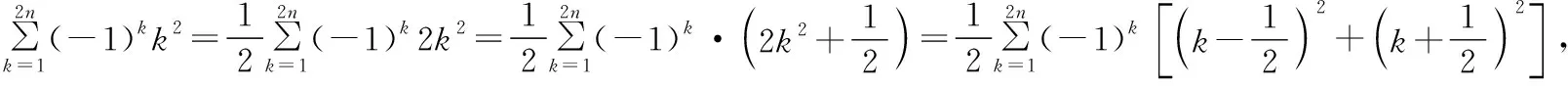
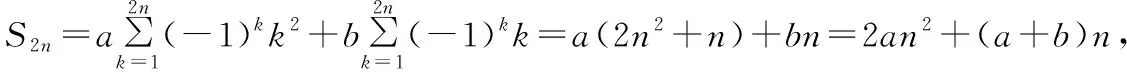
下面运用模型4来求解例5(Ⅱ)问.

解法2：

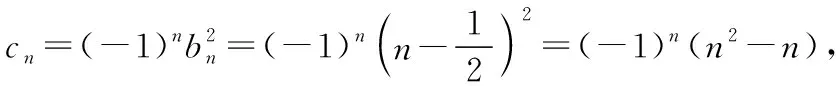
四、方法反思

从上面的探究可以知道，等差数列、等比数列、等差数列乘以等比数列、自然数平方和数列、自然数立方和数列都可以利用裂项求和的方法求得.事实上可以构造出无数个能用裂项求和的数列，但回归到本质，这些数列通项都可以化简为an=f(n+k)-f(n)的形式.教师在教学中教会学生一些简单的数列裂项求和以后，为了让学生解决更加复杂的数列裂项求和问题，应该引领学生探究并归纳一些数列裂项求和模型，一方面可以帮助学生更好地理解数列裂项求和的本质；另一方面，从数学核心素养角度来说，可以更好地培养和提升学生的数学运算与数学建模核心素养.