以形助数突破解三角形中的最值问题
2020-11-15云南唐明超
云南 唐明超
解三角形是高考数学的重点和热点,试题往往聚焦三角形的三边与三角这六个基本元素,以边角关系或是面积关系为背景考查正弦定理与余弦定理,突出考查逻辑推理和数学运算等核心素养.虽然解三角形所考查的核心知识点都较为熟悉,也容易掌握解三角形的基本思路及一般方法,但是在处理三角形的面积、边或角的取值范围等问题时往往存在困难,不能做到准确求解,即使最终能够得出正确答案也需要大量的时间去完成复杂的推理与运算,不能够高效地解决问题.原因是没有充分挖掘问题的几何背景导致对几何性质的运用不能恰到好处,只能依赖于复杂的数学运算与推理过程且费时费力.文章重点阐述解三角形问题中常见的几何背景,分析挖掘几何背景的基本策略,做到准确识别命题意图,找准命题出发点,挖掘问题本质,用好几何性质解决一类三角形基本量的取值范围问题.
类型1 借助三角形的外接圆解决面积的最值问题
例1(2014·全国卷Ⅰ理·16)已知a,b,c分别为△ABC三个内角A,B,C的对边,a=2,且(2+b)(sinA-sinB)=(c-b)sinC,则△ABC面积的最大值为________.

解法评析:试题属于常规的解三角形问题,已知三角形的边角关系,要求灵活选用正弦定理或余弦定理将三角形的边角关系进行转化与化归,进而求解三角形的基本量.在运算过程中既用到了正弦定理和余弦定理,还用到了基本不等式,这些都是解决三角形问题的核心知识点.但是整个解题过程较复杂,难免有小题大做的嫌疑,这是完全依赖于代数运算的不足之处.如能认真思考问题背后所隐藏的几何特征,充分挖掘几何背景,实现以形助数,便可轻松破解该问题.
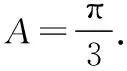

解法评析:几何法充分利用了问题背后所隐藏的外接圆这一背景,将复杂的代数运算进行优化,只需要直接观察图形中动点的变化情况,根据几何关系直观判断,以形助数,则可快速得出结果.法2明显优于法1,解题效率也更高,掌握该方法对于发展学生的抽象概括能力与数学建模核心素养更为有利,这也真正体现了试题的育人价值.

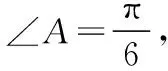
类型2 以阿波罗尼斯圆为背景的三角形面积问题

解析:试题中的边角关系明确,可以借助余弦定理得出三角形一个内角的余弦值的表达式,进而利用三角恒等变换得出其正弦值的表达式,再用面积公式得出三角形面积的表达式,最后将面积看成是边长的函数并利用函数的单调性得出三角形面积的最大值,具体解答过程如下.

解法评析:基于余弦定理与面积公式实现边角关系的转化,再借助三角恒等变换与函数的单调性进行解答虽然属于常规解法,具有起点低、容易入手等特点,但是运算过程较复杂,对数学运算能力要求较高,解题所需时间较长,不是较优解法,需要改进.
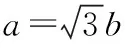
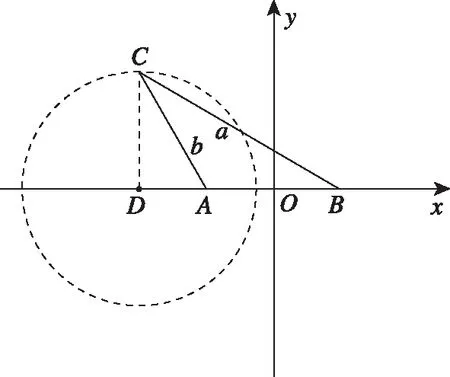
解法评析:充分挖掘问题背后隐藏的几何特征,将数量关系几何化,给数量关系找到恰当的几何载体,可以化抽象为直观,化难为易,有效降低运算难度,快速解决问题.阿波罗尼斯圆是一个联系数量关系与几何特征的典范,也是数学史上的一个重大发现,借助阿波罗尼斯圆解决三角形面积的最值问题对发展学生的数学建模核心素养具有重要意义,也有利于学生了解数学文化,掌握知识的发生与发展逻辑.
类型3 以四边形外接圆为背景的解三角形问题

(1)求DC;

解析:试题所呈现的是有一条公共边的两个三角形复合而成的四边形问题,本质还是解三角形,灵活用好正弦定理与余弦定理可以完成对该题的解答,这也是解三角形的常规思路和一般方法.
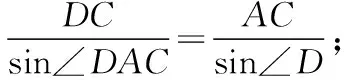

解法评析:常规解法的特点是容易入手,起点较低,但是要能顺利解决问题往往需要通过复杂的推理与运算过程,而且在运算的过程中容易出现错误.本题的关键是四边形内角B与角D互补,而且∠BAC=45°,∠DAC=60°均属于特殊角,如能基于该条件大胆猜想公共边是该四边形外接圆的直径,解答过程将会更加简洁,具体解答过程如下.
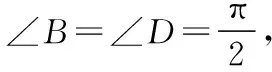
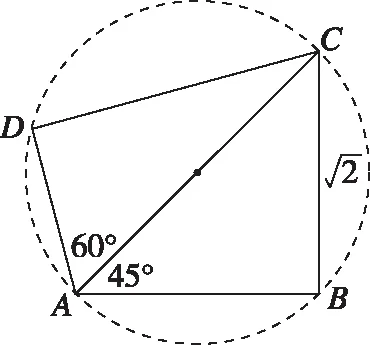
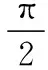
类型4 以椭圆为背景的解三角形问题
例4在△ABC中,a,b,c分别为三个内角A,B,C的对边,已知a+c=2b,则角B的取值范围为________.

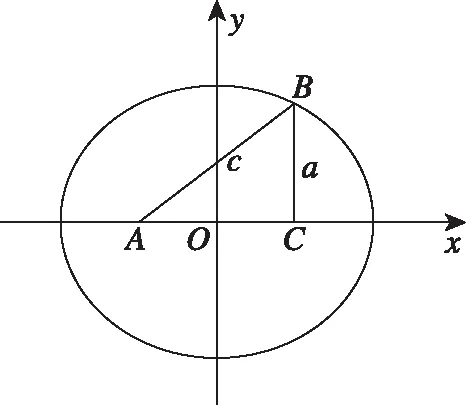
解法评析:没有经过复杂的推理运算便可得出正确答案,这就是挖掘并用好几何性质的重要价值,这与命题者的构题思路不谋而合,所以准确识别命题者的命题意图,挖掘命题的出发点以及试题背后的几何关系是解决问题的最佳途径.
学必有法而学无定法,重难点问题的突破绝不能单一地依靠重复的解题训练来完成,还需要尝试挖掘问题的本质属性,基于已有知识经验寻找知识点之间的逻辑联系,揣测命题意图以及探究试题背后所隐藏的数学本质,尽可能地契合命题者的思想,在解决问题的过程中实现知识与能力的双重提升.数缺形时少直观,形缺数时难入微,这是数形结合思想的重要意义.数学的学习过程关键在于悟,要学会感悟知识的发生与发展的过程,体会知识间的逻辑联系,构建数学知识体系,最终达到能综合运用所学知识高效解决实际问题的目的.这也正是新课标中要学会用数学的眼光观察世界,用数学的思维思考世界的具体要求.以形助数,以数辅形是数学知识的本质属性,学会挖掘变化的问题背后所隐藏的不变的数学本质是数学学习的重要任务.这不仅可以提高解题效率,更重要的是能更好地提高数学核心素养,优化数学思维,形成适应社会发展所必需的关键能力和必备品格.
