启发学生思考,培养学生质疑精神之实践
——以错题研究为例
2020-11-15广东
广东 李 虎
近几年,高考试题越来越新颖多变,考查方向也从能力立意转向核心素养立意,课堂教学也应该随之改变,一味题海战术,刻板训练未必会有好的效果,课堂更应该打开学生思维,以一种开放的状态,培养学生的质疑精神和创新意识.不仅要关注为什么要这样做,更应该关注自己错在哪里.下面笔者就以课堂教学中学生提出的几个很有意义的质疑为契机,谈谈一些浅薄的认识.
一、发扬“最后一问”
【例1】已知数列{an}的前n项和为Sn,并且4Sn=(an+1)2,求{an}的通项公式.
思维导航:本题考查数列的通项公式和前n项和的关系,消去Sn得到递推公式,然后根据递推公式即可解出通项公式.
解答过程:由4Sn=(an+1)2①,取n=1得4a1=(a1+1)2,解得a1=1,以n+1替换n得4Sn+1=(an+1+1)2②,②-①得4an+1=(an+1+1)2-(an+1)2,整理得(an+1+an)(an+1-an-2)=0 ③.所以an+1+an=0或an+1-an-2=0,所以数列{an}为等差或等比数列.解得an=(-1)n-1或an=2n-1.
笔者任教的两个班级绝大部分学生是这样解答的,参考答案也是这样给的.笔者在评讲时,问有没有其他解法.有个学生举手,老师这是一个错题,原因如下:先求a1=1,把a1=1代入得到4(1+a2)=(a2+1)2,解得a2=-1或a2=3;再分两种情况代入求得a3=1或a3=-3或a3=5;再分情况代入,求得a4=-1或a4=3或a4=-5或a4=7;….
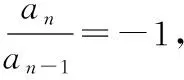
反思:在教学中,要发扬“最后一问”的精神,问问学生们,还有没有想要说的,有没有其他的想法和思路,培养学生的质疑精神,不盲信答案或者参考资料.本题在多份参考资料里出现,基本都是错误的解答.
二、错在哪?
【例2】设函数f(x)对任意的x∈R,y∈R都满足f(x+y)=f(x)f(y)+2,且f(1)=2,则f(n)=________(n∈N*).
思维导航:本题是一道典型的抽象函数题目,考查由抽象函数得到数列的递推公式,然后根据递推公式求解通项公式.
解答过程:取x=n,y=1得f(n+1)=f(1)f(n)+2,即f(n+1)=2f(n)+2,f(n+1)+2=2(f(n)+2),所以{f(n)+2}是以4为首项,2为公比的等比数列,解得f(n)=2n+1-2.
在测试卷中,有60%的人是这个结果,这个解答也是答案中给出的结果.还有20%的人结果是f(n)=2.在试卷评讲过程中,笔者让一位学生来讲解他的思考过程,给出的解答过程如下:
取x=0,y=1得f(1)=f(0)f(1)+2,将f(1)=2代入得f(0)=0,再取x=0,y=n可得f(n)=2.
讨论辨疑:学生A:这个题目是个错题,取x=y=1得f(2)=f(1)f(1)+2=6,再取x=y=2得f(4)=f(2)·f(2)+2=38 ④,取x=1,y=2得f(3)=f(1)f(2)+2=14,再取x=1,y=3得f(4)=f(3)f(1)+2=30 ⑤.④⑤两式矛盾,说明不存在这样的函数.
学生B:若取x=y=0则得f(0)=(f(0))2+2,此方程没有实数根,说明这个函数在x=0无定义,由x,y的任意性可得这样的实值函数不存在.
反思:在发现问题时,不妨多留点时间给学生们,让他们自己去发现问题所在,在质疑中提升思维的品质,在辨疑中串联知识点,提升思维的深度和知识的厚度.
三、这样的函数存在吗?
【例3】定义在R上的函数f(x)的导函数为f′(x),若对任意的实数x,有f(x)>f′(x),且f(x)+2 017为奇函数,则不等式f(x)+2 017ex<0的解集是________.
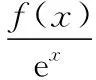
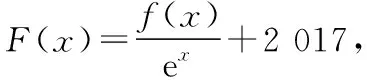
最后一问:从上面的解答过程看,f(x)+2 017为奇函数这个条件,这里只用到了f(0)+2 017=0,题目给的条件貌似过强,会不会出现条件之间的不相容性,这样的函数根本不存在呢?简单来说,满足上述条件的f(x)存在吗?

四、题目是否真的少条件?

(Ⅰ)证明:AB⊥平面ADE;
(Ⅱ)求二面角E-BC-F的余弦值.

背景:此题是2019年广东省模拟试卷理科数学第18题,本班某学生听说高三学姐刚考完的省一模很难,年级均分才八十多分,于是去借了试卷来做一下.在大题的第二问就卡住了,班上几个同学商量后,一致认为题目少了条件,不然做不出来.拿来请教笔者,笔者看到此题有一种似曾相识的感觉,发现此题和2016年高考全国卷Ⅰ理科数学第18题如出一辙.原高考题如下:
(2016·全国卷Ⅰ理·18)如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.
(Ⅰ)证明:平面ABEF⊥平面EFDC;
(Ⅱ)求二面角E-BC-A的余弦值.
依稀记得当年这道考题,全省73.3万考生,根据阅卷情况,能拿到满分的人寥寥无几,当年学生出考场后也同样认为少了条件,为什么同样的情景会重现?
解疑:笔者问学生,你能得到AB∥CD吗?学生答:就是卡在这里,题目应该给出这个条件.那么,CD是否平行EF?学生答:平行啊.那么,CD是否平行平面ABFE?学生答:平行.学生马上说:知道了,明白了.
反思:线面平行的性质定理平时用的较少,很多学生会忽视用线面平行可以得到线线平行,造成第一问都做不出来.由于已知条件是二面角F-AB-C的大小为30°,在第一问做不出来的情形下,第二问也如空中楼阁,无法建系来计算.本题在高三考生中得分也非常低.在高考题转变为以核心素养立意后,高三复习要注意回归“课本”,夯实基础,这样才会在变化中寻找到规律.
【例5】关于圆周率π,数学发展史上出现过许多有创意的求法,如著名的普丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计π的值:先请120名同学每人随机写下一个x,y都小于1的正实数对(x,y),再统计其中x,y能与1构成钝角三角形三边的数对(x,y)的个数m,最后根据统计个数m估计π的值.如果统计结果是m=34,那么可以估计π的值为
( )

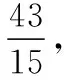
反思:考完学生反思才发现,漏掉了构成三角形这一基本条件.本题要考查的知识点是随机模拟,用频率估计概率.涉及几何概型、线性规划、余弦定理、构成三角形条件等相关知识.同时又联系数学史料,是这几年命题的热点和新方向.
五、数形结合,边思边画

( )

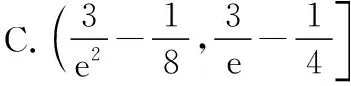
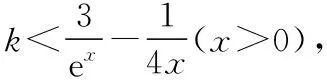


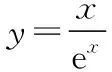

( )
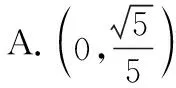

背景:此题为七校联合体高二联考试题第11题,此题得分率仅为24%.很多学生不能将问题转化为函数交点问题.

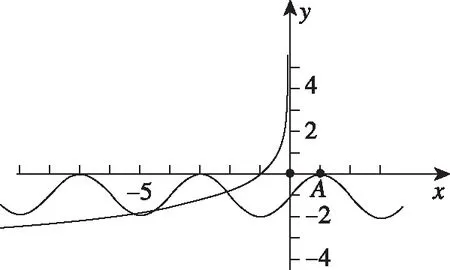
学生质疑:对比上述两题,都是用数形结合解决,但是一个是直线与曲线,一个是曲线与曲线.曲线与曲线相交,是否一定要当x=-5时,y=loga(-x)(x<0)在y=-2的上方?是否会出现在最低点(x=-5)的右侧“附近”就可以有两个交点?
反思:从学生质疑来看,对于这道选择题,选A没问题,是否A的右端是上界,可以借助几何画板模拟一下.将几何画板的精度设置为最高.

六、把握高考新动向,科学备考
(Ⅰ)从游客中随机抽取3人,记总得分为随机变量X,求X的分布列与数学期望;
(Ⅱ)(ⅰ)若从游客中随机抽取m人,记总分恰为m分的概率为Am,求数列{Am}的前10项和;
(ⅱ)在对所有游客进行随机问卷调查过程中,记已调查过的累计得分恰为n分的概率为Bn,探讨Bn与Bn-1之间的关系,并求数列{Bn}的通项公式.
背景:本题根据2019-2020学年度武汉市部分学校新高三起点质量检测第21题改编.改编的目的是为了在试题中加入家国情怀知识,让学生对家乡更了解,也是思政教育的一种渗透.
反思:本题第二问的第二小问,全级理科928名考生无人做出.可以看出本题是根据2019年高考全国卷Ⅰ概率与统计题改编设计,属于概率与数列结合题目,比较新颖.
结束语:学生会提出问题,说明他们在思考,无论对与错,都反映他们对知识的一种理解,教师要做的,就是把这些“火花”变成燎原之势,那将迸发无限的希望.同时,教师要关注高考新动向,及时把握时代的步伐,注意命题的动向,科学高效备考,为学生指明高考复习备考的方向.
