用空间向量速求二面角的几种方法
2020-11-15江西毛乐萍
江西 毛乐萍
利用空间向量求二面角,思路切入快,但常规方法运算量大,过程比较复杂,容易出错,是学生的常见失分点.在某些条件下,可以采用更简单的运算,快速求出结果,下面笔者介绍几种方法.
一、运用截距法速求平面的法向量

用常规求法向量的方法易证,证明过程略.下面举例来说明截距法的运用.
【例1】(2019·天津卷·理17)如图,AE⊥平面ABCD,CF∥AE,AD∥BC,AD⊥AB,AB=AD=1,AE=BC=2.
(Ⅰ)求证:BF∥平面ADE;
(Ⅱ)求直线CE与平面BDE所成角的正弦值;


解析:(Ⅰ)证明略.



评析(Ⅱ)中若用传统求法向量的方法,则需要设法向量的坐标,利用法向量与平面中两个不共线向量的数量积为零列方程组,求得法向量,过程比较麻烦,运算量大.而运用截距法求平面的法向量,只需要知道平面在坐标轴上的截距就可以直接得出法向量,不需要计算,大大减少了运算量,且提高了运算的准确度.(Ⅲ)中若用列方程组的方法求法向量,不仅法向量是未知的,且点F的坐标中也含有未知数,更增加了运算量与难度,而运用截距法求平面的法向量,求出了截距之后,法向量一步就到位,绕开了求含参数的方程组,快速得到法向量,顺利求得结果.
二、利用二面角的定义,不求法向量
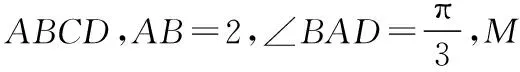

(Ⅰ)求PO的长;
(Ⅱ)求二面角A-PM-C的正弦值.

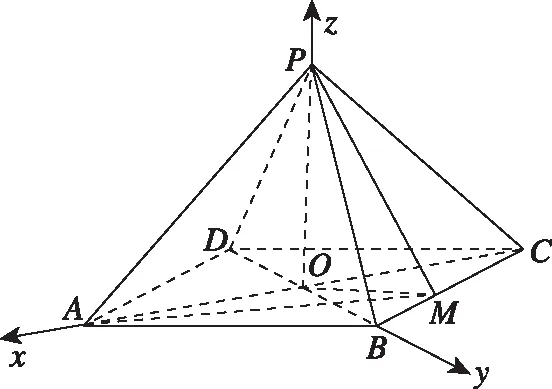
评析在二面角的两个半平面内若能分别找到垂直二面角的棱的直线,由二面角的定义,则可以转化为求这两直线的方向向量所成的角,不需要在三角形中用余弦定理求解,也不需要求两平面的法向量,简化了运算过程,大大减少了运算量,同时可以提高运算的效率,可以快速求出结果.
三、利用共线向量找等效向量
【例3】如图,在四棱锥P-ABCD中,PA⊥AD,底面四边形ABCD为直角梯形,AD=λBC,AD∥BC,∠BCD=90°,M为线段PB上一点.
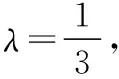
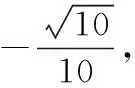

解析:(Ⅰ)延长BA与CD交于点N,由线面平行的性质定理易知存在点M为线段PB上靠近点P的三等分点.



四、利用等效平面
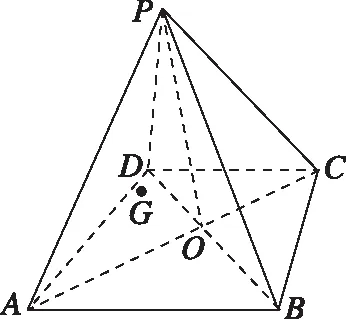
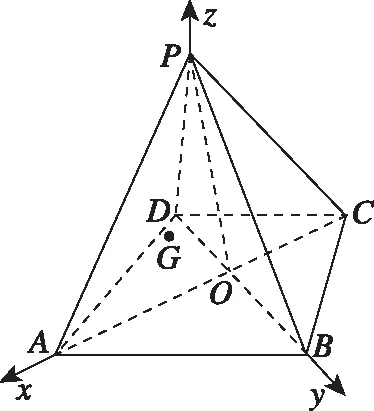
【例4】如图,在四棱锥P-ABCD中,△ABD是正三角形,△BCD是等腰三角形,∠BCD=120°,PC⊥BD.
(Ⅰ)求证:BP=DP;
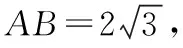

解析:(Ⅰ)连接AC交BD于点O,∵△ABD为正三角形,△BCD是等腰三角形,
∴AC⊥BD且O为BD的中点.由已知PC⊥BD,PC∈平面APC,可得BD⊥平面APC.
∴BD⊥PO.又∵O为BD的中点,∴△PBD为等腰三角形,即PB=PD.




利用空间向量解立体几何不是难点,但却是高考重点考查内容,因为计算量大而容易出错,要重视方法的总结与积累,减少运算量,提高运算的准确度.
